Составляем систему алгебраических уравнений методом узловых напряжений, согласно первому закону Кирхгофа.
I1+J4-I2=0
I2-I3-I4=0
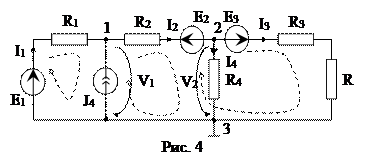
4. V1,V2 – узловые напряжения узлов 1 и 2 соответственно. Выражаем токи ветвей через узловые напряжения на основе 2 закона Кирхгофа для вспомогательных контуров, которые обязательно проходят через базисный узел, и закона Ома:
I1∙R1+V1 =E1, I2∙R2+V2-V1= -E2, I3∙(R3+R)-V2 =E3 (V=U).
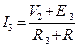
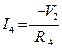
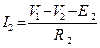
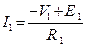
После подстановки формул токов данная система уравнений переводится в систему узловых уравнений, записанную в канонической форме. Число уравнений должно быть равно числу неизвестных узловых напряжений.
Для 1 уравнения получим 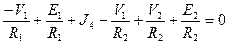
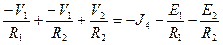 . Затем можно поменять знаки и получить уравнение
. Затем можно поменять знаки и получить уравнение  . Аналогично для 2 уравнения получим
. Аналогично для 2 уравнения получим
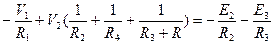 . Эти уравнения приводят к стандартному каноническому виду:
. Эти уравнения приводят к стандартному каноническому виду:
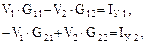
где  – это собственные проводимости соответственно узлов 1 и 2.
– это собственные проводимости соответственно узлов 1 и 2.
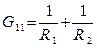 .
.
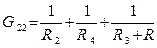 .
.
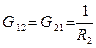 – взаимные проводимости между узлами 1 и 2.
– взаимные проводимости между узлами 1 и 2.
IУ1, IУ2 – собственные или задающие узловые токи, соответственно, независимых узлов 1 и 2. В общем виде их можно представить в следующем виде:
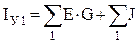 ,
,
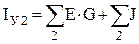 ,
,
где 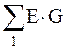 – алгебраическая сумма произведений ЭДС ветвей, примыкающих к узлу 1, на их проводимости,
– алгебраическая сумма произведений ЭДС ветвей, примыкающих к узлу 1, на их проводимости, 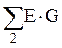 – алгебраическая сумма произведений ЭДС ветвей, примыкающих к узлу 2, на их проводимости; при этом со знаком "+" берутся те ЭДС, которые действуют в направлении узла, и со знаком "–" – в направлении от узла;
– алгебраическая сумма произведений ЭДС ветвей, примыкающих к узлу 2, на их проводимости; при этом со знаком "+" берутся те ЭДС, которые действуют в направлении узла, и со знаком "–" – в направлении от узла; 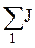 – алгебраическая сумма токов источников тока, присоединенных к узлу 1,
– алгебраическая сумма токов источников тока, присоединенных к узлу 1, 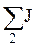 – алгебраическая сумма токов источников тока, присоединенных к узлу 2; при этом со знаком "+" берутся те токи, которые направлены к узлу, а со знаком "–" в направлении от узла. Для нашего случая токи IУ1, IУ2 имеют следующий вид:
– алгебраическая сумма токов источников тока, присоединенных к узлу 2; при этом со знаком "+" берутся те токи, которые направлены к узлу, а со знаком "–" в направлении от узла. Для нашего случая токи IУ1, IУ2 имеют следующий вид:
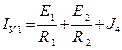 .
.
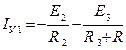 .
.
Узловое напряжение – это напряжение между независимым и базисным узлами и направлено оно к базисному узлу. V1,V2 – узловые напряжения узлов 1 и 2 соответственно. Знак "+" перед узловым напряжением берётся, если это собственное узловое напряжение, в противном случае берётся знак "–".
Данную систему решаем методом Крамера. Составляем определитель второго порядка, в первую и вторую строки которого ставим значения проводимостей стоящих при напряжениях, соответственно в первом и во втором уравнениях нашей системы.
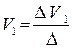 Затем составляем определитель
Затем составляем определитель 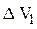 , для этого в определителе
, для этого в определителе 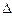 в первом столбе значения проводимостей заменяем значениями токов, стоящих в правой части нашей системе.
в первом столбе значения проводимостей заменяем значениями токов, стоящих в правой части нашей системе.
После чего вычисляем напряжение  по следующей формуле:
по следующей формуле:
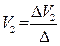 Аналогично находим напряжение
Аналогично находим напряжение 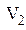
6. Находим токи ветвей через узловые напряжения:

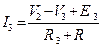
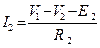

Общая форма записи системы уравнений по МУН с узловыми напряжениями (потенциалами) VK, собственными проводимостями узлов GKK, взаимными проводимостями между узлами GKM и узловыми токами.

Переменные токи и напряжения
Основные понятия и параметры
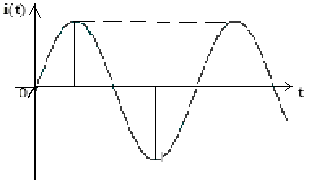 Под переменным током или напряжением понимают ток или напряжение, меняющееся периодически по гармоническому закону косинуса или синуса.
Под переменным током или напряжением понимают ток или напряжение, меняющееся периодически по гармоническому закону косинуса или синуса.
i(t)=Im ·cos(w∙t+ji),
где Im – амплитуда тока;
ji - начальная фаза тока [рад](равна- π/2, так как для косинуса отсчет идет от положительного максимума и по оси с +),
w∙t+ji – мгновенная фаза в момент времени t.
ω = 2π∙f [рад/с] – угловая частота, f – циклическая частота [Гц]
Т - период колебания 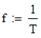
Дата добавления: 2016-03-15; просмотров: 1107;
