В) Проектирование по первому и второму пути переходных кривых различной длины.

Рассмотрим два возможных случая взаимного расположения первого и второго путей.

1) Второй путь по отношению к первому пути находится внутри кривой (рисунок 8.2.3).

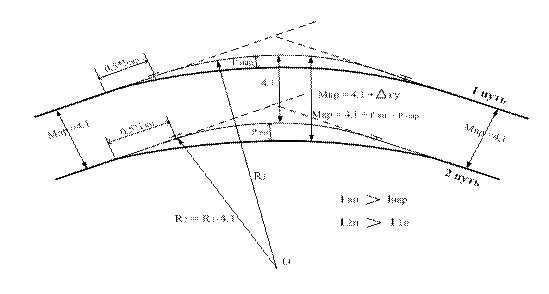
Рисунок 8.2.3 –

Радиус концентрической кривой второго пути определится как:

R₂ = R₁ – 4,1 , (8.2.2)

где R₂ – радиус круговой кривой второго пути, м; R₁ – радиус круговой кривой первого пути, м.

Величина междупутья на прямых подходах – 4,1 м.

Согласно формуле (8.2.1) величина междупутья в кривой М_кр = 4,1 + ∆_гу.

Из рисунка видно, что после постановки переходных кривых междупутье в кривой определится по следующей зависимости:

М_кр = 4,1 + р_вн – р_нар , (8.2.3)

где р_вн, р_нар – сдвижка от переходной кривой, соответственно, по внутреннему и наружному пути, м.

Сопоставляя выражения (8.2.1) и (8.2.3), находим:

р_вн – р_нар = ∆_гу. (8.2.4)

В рассматриваемом случае: р_вн = р_{2 пути}, р_нар = р_1пути.

Сдвижка от переходной кривой может быть определена как:

р = l² / (24·R), (8.2.5)

где l – длина переходной кривой, м.

В рассматриваемом случае выражение (8.2.4) примет вид:

(l_2пути)² / (24·R₂) – (l_{1 пути})² / (24·R₁) = ∆_гу. (8.2.6)

Отсюда,

l_2пути = (24·R₂ · (∆_гу + (l_{1 пути})² / (24·R₁)))^1/2.

2) Второй путь по отношению к первому пути находится снаружи кривой (рисунок 8.2.4).

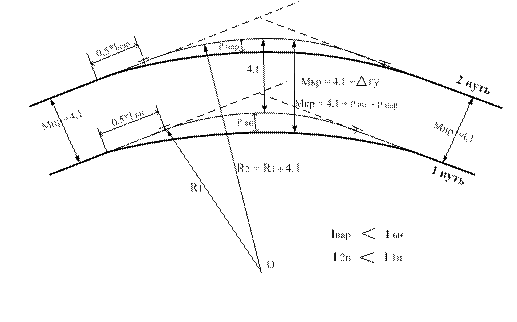
Рисунок 8.2.4 –

Радиус концентрической кривой второго пути определится как:

R₂ = R₁ + 4,1. (8.2.7)

Выражение (8.2.4) примет вид:

р_1пути – р_{2 пути} = ∆_гу.

Выражение (8.2.6) преобразуется следующим образом:

(l_1пути)² / (24·R₁) – (l_{2 пути})² / (24·R₂) = ∆_гу.

Отсюда,

l_2пути = (24·R₂ · ((l_{1 пути})² / (24 · R₁) – ∆_гу ))^1/2.

В рассмотренных случаях 1) и 2) закономерность одна: длина переходной кривой внутреннего пути больше длины переходной кривой наружного пути. Именно эта закономерность позволяет создать в кривой увеличение расстояния между осями первого и второго путей т.е. обеспечивает габаритное уширение междупутья.

Данный метод широко распространен и, безусловно, может считаться основным на сети железных дорог России.