Порядок решения задачи изменения ширины междупутья на прямом участке пути (сход в прямой).

1) Анализ и контроль исходных данных.

Сначала следует выбрать схему схода: определить взаимное расположение первого и второго пути (второй путь слева или справа от первого, ориентируясь по ходу пикетажа), величину начального и конечного междупутья. Кроме того, следует определить пикетажное значение либо начальной, либо конечной точки схода и установленные скорости движения на данном участке.

Крайне желательно изобразить выбранную схему графически для лучшего представления задачи.

2) Определение параметров плана

Так как сход в прямой представляет собой две кривые, направленные в разные стороны, то под параметрами схода следует понимать:

- угол поворота, радиус круговой кривой, длину переходной кривой - для первой кривой;

- угол поворота, радиус круговой кривой, длину переходной кривой - для второй кривой;

- длину прямой вставки между первой и второй кривой.

Для упрощения расчетов можно назначать величины радиусов и длины переходных обоих кривых второго пути одинаковыми; угол поворота этих кривых будет один и тот же т.к. пути параллельны.

Величину радиуса кривых (R₁ = R₂ = R) назначаем самостоятельно, исходя из условия обеспечения скоростей движения на участке схода.

Длину переходной кривой (l₁ = l₂ = l) определяем по условию обеспечения нормативного отвода возвышения наружного рельса.

Длину прямой вставки (b) определяем по нормативам /СТН Ц 01-95, табл.7/

Угол поворота вычисляем, используя тригонометрические зависимости по рисунку 8.2.6:

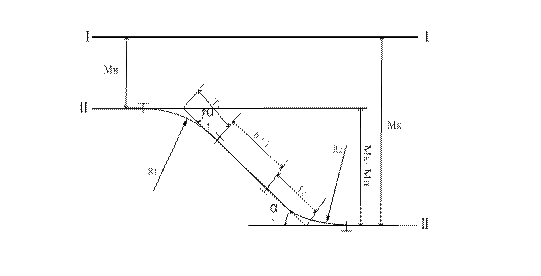
Рисунок 8.2.6 –

tg (α/2) = 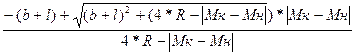. (8.2.10)

Угол поворота (α1 = α2 = α) получим как:

α = 2*(arctg ( 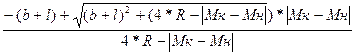)). (8.2.11)

Полученную величину угла округляем до минут и всегда в меньшую сторону!

Таким образом, все параметры плана схода на прямой определены.

3) Определение пикетажа характерных точек.

Определение пикетажа характерных точек кривой начинаем с определения положения начальной (нулевой) точки. Этой точкой будет заданная точка начала или конца схода. Как правило, задается в качестве исходной начальная точка схода, её и будем считать нулевой.

Начинается сход с начала входной переходной кривой в первой кривой (НПК₁), следовательно (рисунок 8.2.7):

Рисунок 8.2.7 –

НПК₁= 0.

Следует учесть:

– для дальнейших расчетов, в которых положение всех характерных точек определяется в делениях кривой (дам), следует величины l, b и Т перевести в дам т.е. разделить на 10;

– в пикетажное значение характерных точек кривых, не лежащих на прямой, параллельной первому пути: ККК₁, КПК^/₁, НПК^/₁, НПК₂, НКК₂, КПК₂, ККК₂ следует вносить поправку т.е. учитывать проекции соответствующих отрезков на ось первого пути.

Тогда по формулам находим:

НКК₁ = НПК₁ + 0,5· l;

КПК₁ = НКК₁ + 0,5· l;

ККК₁ = НКК₁ + Т +Т·cosα;

КПК^/₁ = ККК₁ – 0,5· l · cosα;

НПК^/₁ = ККК₁ + 0,5· l · cosα;

НПК₂ = НПК^/₁ + b· cosα;

НКК₂ = НПК₂ + 0,5· l · cosα;

КПК₂ = НКК₂ + 0,5· l · cosα;

ККК₂ = НКК₂ +Т +Т·cosα;

КПК^/₂ = ККК₂ – 0,5· l;

НПК^/₂ = ККК₂ + 0,5· l.

4) Определение проектных стрел.

Под проектными стрелами будем понимать стрелы всего участка схода на прямой: от точки НПК₁ до точки НПК^/₂.

Согласно методике определения стрел, имеем:

стрела в первой круговой кривой второго пути (F₁)и стрелаво второй круговой кривой второго пути (F₂) будут равны т.к. равны радиусы и их значение определится как:

F₁ = F ₂ = F = (500 · а²) / R.

Проектные стрелы в каждой их двух кривых по второму пути определяются по тем же формулам, что и в задаче выправка кривой.

i – номер точки

если 0< i < НПК₁ F i = 0;

если НПК₁< i < КПК₁ F i = (F / l) · (i – НПК₁);

если КПК₁< i < КПК^/₁ F i = F;

если КПК^/₁< i < НПК^/₁ F i = (F / l) · (НПК^/₁ – i); (8.2.12)

если НПК^/₁< i < НПК₂ F i = 0 – прямая вставка

если НПК₂< i < КПК₂ F i = – (F / l) · (i – НПК₂);

если КПК₂< i < КПК^/₂ F i = – F;

если КПК^/₂< i < НПК^/₂ F i = – (F / l) · (НПК^/₂ – i);

если НПК^/₂< i < конец схода F i = 0.

Следует помнить, что знаки стрел в первой и второй кривой – противоположны.

5) Определение сдвигов (смещений) проектируемого пути относительно фиктивной оси базисного пути.

Согласно теории нормалей /4/ смещение оси проектируемого пути (у_i) относительно фиктивной оси базисного (первого) пути в любой точке определяется как:

у_i = ∑∑2· (F_2i – F_1i)

Но так как первый путь – прямая (т.е. стрелы по первому пути – нулевые) выражение принимает вид:

у_i = ∑∑ 2· F_2i (8.2.13)

Вычисление смещений оси проектируемого пути (у_i) обычно производится в табличной форме.

6) Определение разбивочных междупутий.

Итогом расчета схода в прямой помимо параметров кривой второго пути, пикетажа характерных точек являются также величины разбивочных междупутий (М_i), позволяющие вынести ось второго пути на местности.

Разбивочные междупутья от первого пути определяются следующим образом:

М_i = М_нач + у_i . (8.2.14)

Вычисление разбивочных междупутий М_i обычно производится в табличной форме.