Линейные системы кольцевого тестирования.

Рассмотрим принцип построения линейных последовательных систем (ЛПОС) кольцевого тестирования (КТ), применение которых наиболее целесообразно для встроенного диагностирования.

Рассматриваемые ЛПОС представляют собой строго периодическую автономную систему, имеющую циклический характер функционирования. В литературе вопросы синтеза автономных систем занимают мало места. В первую очередь это связано с ограниченным их использованием. В диагностике наибольшее применение автономные системы нашли при порождении и интерполировании тестов. Именно построение автономной ЛПОС обеспечивает простоту реализации КТ, что в конечном итоге делает ЛПОС одной из эффективных систем компактного тестирования.

Рассмотрим КТ комбинационного дискретного устройства (ДУ), которое является простым объектом тестирования. Из опыта практических разработок систем компактного тестирования достаточно хорошо известно раздельное применение генераторов и анализаторов, реализованных на счетчиках и регистрах. В системах кольцевого тестирования комбинационного ДУ механизм совмещения функций генератора и анализатора как в пространстве, так и во времени осуществляется наиболее просто.

Пусть ДУ имеет 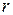входов и 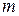выходов и описывается системой булевых функций:

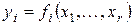
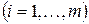. (3.1)

Линейная последовательная система (рис.1.2) содержит комбинационное корректирующее устройство КУ, 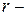разрядный сдвиговый регистр Рг r, схемы свертки выходов по mod 2 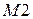. Назначение КУ состоит в аппаратурной линеаризации ДУ, в результате которой на выходе 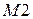формируется линейная функция обратной связи

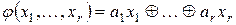. (3.2)

Посредством обратной связи, реализуемой соединением выхода 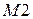со входом последовательного занесения кода в регистр Рг r, последний совмещает функции генератора теста и анализатора ответов ДУ на тест. Таким образом, для системы характерно наличие линейной функции обратной связи и последовательного анализа результатов тестирования.

Процесс тестирования ДУ осуществляется в моменты 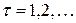под действием тактовых импульсов сдвига Рг r и при исправности ЛПОС описывается рекуррентным уравнением:

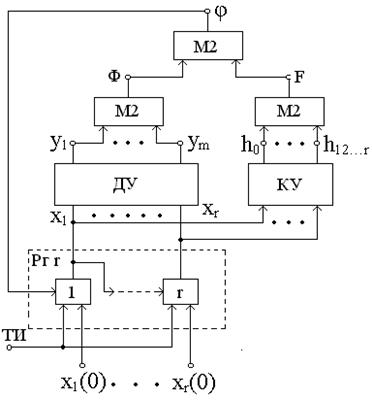
Рис.3.2. Линейная система кольцевого тестирования.

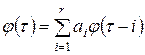. (3.3)

Суммирование проводится по mod 2. Начальные условия 3.3 задаются набором значений:

, , , ,

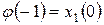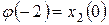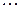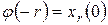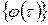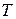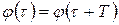соответствующих начальному состоянию Рг r. Будем рассматривать строго периодические ЛПОС. Это означает, что для последовательности , представляющей собой решение уравнения 3.3, существует такое натуральное значение , что для любого .

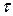Для анализа периодичности ЛПОС используются свойства кольца многочленов над полем 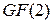. По определению многочлен от одной переменной может быть записан в виде последовательности

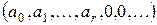
с элементами из 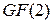. Чаще применяют другую запись многочлена:

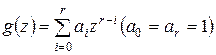. (3.4)

Если 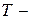наименьшее целое положительное число, для которого 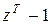делится на многочлен 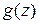, то решение уравнения 1.3 периодично с периодом 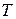, а совокупность периодических решений совпадает с идеалом, порождённым многочленом ( 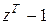)/ 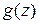в алгебре многочленов 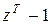. Таким образом, период системы отождествляется с показателем 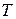, которому принадлежит неприводимый многочлен обратной связи .

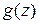Основу синтеза ЛПОС периода 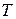составляет синтез КУ. Заданием на синтез КУ служит функция обратной связи 1.3, определяемая набором коэффициентов 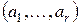многочлена (3.4).

Из выше сказанного следует, что если ДУ описывается системой булевых функций 3.1, то для того, чтобы построить КУ, нужно найти сумму функций ДУ:

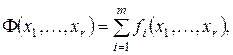
которую выражают многочленом Жегалкина:

,

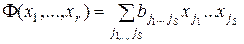где 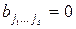или 1, а суммирование выполняется по всем подмножествам 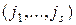множества 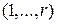. Представление функции 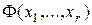в виде многочлена Жегалкина позволяет выявить свойства, связанные с линейностью и нелинейностью ДУ. Для получения этого многочлена необходимо определить коэффициенты-решения 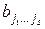системы уравнений над :

;

;

…………………

;

…………………

;

…………………

;

………………...

.

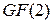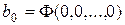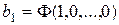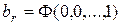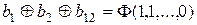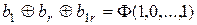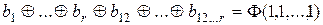Свободные члены системы определяются вычислением значений функции 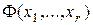на всех 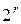наборах аргументов. Решение системы может быть получено применением метода Гаусса.

Сформулируем задание на синтез КУ со схемой 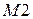на выходе:

,

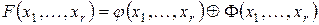Поскольку функция 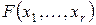оказывается выраженной многочленом Жегалкина, то в общем случае для реализации её слагаемых

,

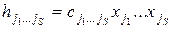где 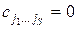или 1, 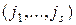— подмножества множества 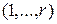, корректирующее устройство содержит соединения и схемы совпадения. Их выходы подключаются ко входам 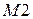(рис.3.2). Известно, что при тестировании линейного ДУ или нелинейного ДУ с линейной функцией 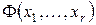корректирующее устройство не содержит схем совпадения и состоит только из соединений выходов Рг r со входами 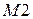. В частном случае КУ может отсутствовать.

В процессе функционирования ЛПОС на входах ДУ формируются двоичные наборы 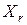, согласно рекуррентному соотношению

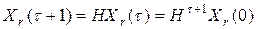
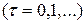, (3.5)

где 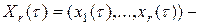вектор-столбец;

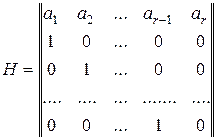
— сопровождающая матрица неприводимого многочлена 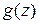. При исправности ЛПОС в силу того, что 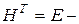единичная матрица, из 5.5 имеем:

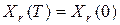
Это даёт возможность устанавливать факт исправности ДУ можно посредством наблюдения одинаковых состояний (выходов) Рг r до и после тестирования. В процессе тестирования Рг r устанавливается в начальное состояние, затем подаётся 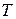тактовых импульсов, и, если система после Т тактовых импульсов возвращается в исходное состояние, то принимается решение об исправности ДУ, в противном случае – принимается решение о неисправности ДУ. В этом состоит простота проведения теста, так как нет необходимости в каждом такте анализировать состояние системы.