Кольцевое дублирование последовательностных схем.
Кольцевое дублирование (КД) является одной из разновидностей КТ, использующая эталон 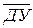 , который включается параллельно ДУ. Данный метод лишён недостатков КТ.
, который включается параллельно ДУ. Данный метод лишён недостатков КТ.
Моделью синхронного дискретного объекта тестирования служит конечный автомат, заданный пятёркой:
(S, 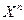 ,
, 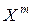 , d, l) (3.9)
, d, l) (3.9)
где S – множество внутренних состояний; n,m – число входов и выходов; 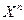 ,
, 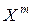 –множества входных и выходных сигналов; d - функция переходов, задающая отображения подмножества множества S
–множества входных и выходных сигналов; d - функция переходов, задающая отображения подмножества множества S 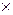
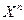 на S; l - функция выходов, задающая отображения подмножества множества S
на S; l - функция выходов, задающая отображения подмножества множества S 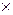
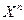 на
на 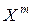 . Принятая модель объекта является достаточно общей, поэтому предлагаемый способ построения ЛПОС ориентирован на достаточно широкий класс дискретных устройств.
. Принятая модель объекта является достаточно общей, поэтому предлагаемый способ построения ЛПОС ориентирован на достаточно широкий класс дискретных устройств.
В состав ЛПОС входят ДУ, КУ, Рг n, М2 (рис3.5). Особенность КУ состоит в том, что в нём содержится 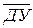 - копия исправного ДУ. Кроме того, КУ содержит регистр Рг e с числом разрядов e и необходимые соединения выходов регистров Рг n, Рг e со входами М2. Период системы характеризуется функцией:
- копия исправного ДУ. Кроме того, КУ содержит регистр Рг e с числом разрядов e и необходимые соединения выходов регистров Рг n, Рг e со входами М2. Период системы характеризуется функцией:
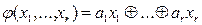
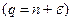 , (3.10)
, (3.10)
где 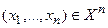 - множество выходных сигналов регистра Рг r, и равен показателю Т неприводимого многочлена
- множество выходных сигналов регистра Рг r, и равен показателю Т неприводимого многочлена 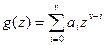
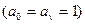 .
.
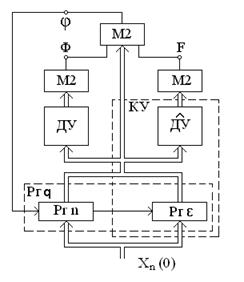
Рис.3.5
Построение ЛПОС КД сводится к построению односумматорного генератора, воспроизводящего строго периодические последовательности. Действительно, пусть Фи F – функции ДУ и 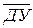 со свёртками М2 на выходах (рис.3.5). Тогда для исправных ДУ и
со свёртками М2 на выходах (рис.3.5). Тогда для исправных ДУ и 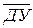 имеет место сравнение:
имеет место сравнение:
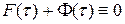
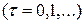 (3.10)
(3.10)
по mod2, а функция обратной связи (7.4) системы реализуется соединениями выходов Рг q со входами М2. Выход i-го разряда Рг q соединяется со входом М2, если  . Установка ЛПОС в начальное состояние производится установкой ДУ и
. Установка ЛПОС в начальное состояние производится установкой ДУ и 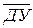 в одинаковые состояния
в одинаковые состояния 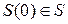 и установкой Рг q в состояние
и установкой Рг q в состояние 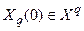 . Так как работа исправной ЛПОС описывается соотношением (3.10), то решение об исправности ДУ принимаются в случае выполнения равенства:
. Так как работа исправной ЛПОС описывается соотношением (3.10), то решение об исправности ДУ принимаются в случае выполнения равенства:
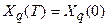 (3.11)
(3.11)
Глава4.
Достоверность кольцевого тестирования для максимального периода.
При кольцевом тестировании (КТ) результат проверки получается при наблюдении поведения автономного генератора, в который преобразуется проверяемый элемент. В тестовом режиме генератор устанавливается в начальное состояние, затем подаются 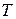 тактовых сигналов, где
тактовых сигналов, где 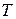 - период генератора. Если конечное состояние генератора совпадает с начальным, то проверяемое устройство считается исправным, в противном случае — неисправным.
- период генератора. Если конечное состояние генератора совпадает с начальным, то проверяемое устройство считается исправным, в противном случае — неисправным.
При проверке исправности в системе КТ из-за отсутствия потактного сравнения фактических ответов ДУ с эталонными ответами существует риск принять неисправное ДУ за исправное. Поскольку решение об исправности принимается в результате сравнения рекуррентной свертки этих ответов с эталоном, то возможно появление неправильных ответов, не изменяющих результата свертки. Подобный риск существует в большинстве диагностических систем, использующих сжатие ответов. Для оценки степени этого риска будем применять такой показатель, как достоверность тестирования.
Множество 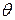 неисправных модификаций ЛПОС разбивается на классы эквивалентности
неисправных модификаций ЛПОС разбивается на классы эквивалентности 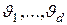 , которые представляются многочленами
, которые представляются многочленами 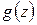
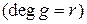 над
над 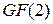 . Тем самым рассматриваются неисправности, преобразующие систему в линейные неисправные модификации. Предполагается, что исправная ЛПОС описывается неприводимым нормированным многочленом
. Тем самым рассматриваются неисправности, преобразующие систему в линейные неисправные модификации. Предполагается, что исправная ЛПОС описывается неприводимым нормированным многочленом 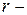 той степени, а появление любого из
той степени, а появление любого из 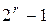 "неисправных" многочленов происходит с вероятностью
"неисправных" многочленов происходит с вероятностью 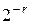 . Здесь
. Здесь 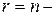 для комбинационного ДУ,
для комбинационного ДУ, 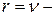 для не зависящего от входа ДУ,
для не зависящего от входа ДУ, 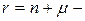 для не зависящего от выхода ДУ,
для не зависящего от выхода ДУ, 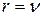 или
или 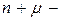 для зависящего от входа и выхода ДУ,
для зависящего от входа и выхода ДУ, 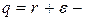 для произвольного ДУ в системе КД. Определим достоверность тестирования в множестве представителей классов
для произвольного ДУ в системе КД. Определим достоверность тестирования в множестве представителей классов 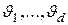 . Для этого достоверность будем находить по формуле:
. Для этого достоверность будем находить по формуле:
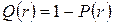 , (4.1)
, (4.1)
где 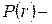 вероятность необнаружения неисправностей, вычисляемая при предположении о равновероятностном появлении дефектов.
вероятность необнаружения неисправностей, вычисляемая при предположении о равновероятностном появлении дефектов.
Имеется несколько методов определения достоверности, но все они сводятся к определению достоверности по формуле (4.1) Таким образом, разница в определении достоверности различными способами заключается в разнице определения вероятности необнаружения неисправностей 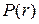 . Рассмотрим эти методы .
. Рассмотрим эти методы .
1. Произведём подсчёт 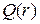 для случая примитивного
для случая примитивного 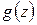 , для которого формула (4.1) допускает нижнюю оценку. В этом случае система тестирования имеет максимальный период
, для которого формула (4.1) допускает нижнюю оценку. В этом случае система тестирования имеет максимальный период 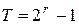 . Поскольку исправность ДУ устанавливается по факту выполнения равенства:
. Поскольку исправность ДУ устанавливается по факту выполнения равенства:
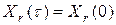
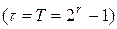 , (4.2)
, (4.2)
то с учётом неисправностей ДУ это равенство будет выполняться для всех неприводимых нормированных многочленов 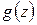
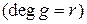 , принадлежащих показателю
, принадлежащих показателю 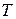 и показателям, являющимся делителями числа
и показателям, являющимся делителями числа 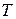 . Число таких многочленов равно:
. Число таких многочленов равно:
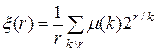 , (4.3)
, (4.3)
где суммирование проводится по всем делителям 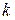 числа
числа 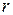 ;
; 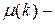 функция Мёбиуса:
функция Мёбиуса:
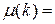 1, если
1, если 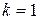 ;
;
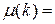 0, если
0, если 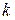 делится на квадрат простого числа;
делится на квадрат простого числа;
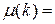
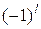 , если
, если 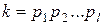 .
.
Формула (1.3) может быть переписана в виде:
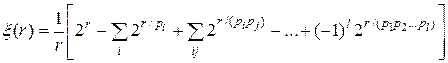 , (4.4)
, (4.4)
где 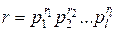 ;
; 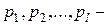 различные простые делители числа
различные простые делители числа 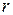 ;
; 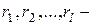 кратность делителей. Учитывая, что появления исправной и неисправной модификаций системы представляют собой равновероятные и взаимоисключающие исходы, для системы максимального периода имеем:
кратность делителей. Учитывая, что появления исправной и неисправной модификаций системы представляют собой равновероятные и взаимоисключающие исходы, для системы максимального периода имеем:
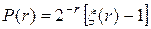 .
.
2. Второй способ отличается от первого иным определением 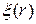 . А сама достоверность рассчитывается по формуле:
. А сама достоверность рассчитывается по формуле:
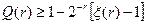 . (4.5)
. (4.5)
Если решение об исправности ДУ принимается по результату выполнения равенства (3.11) в такте 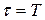 и невыполнения в тактах
и невыполнения в тактах 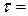 1,2,…,
1,2,…, 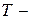 1, то неисправные модификации системы с примитивным многочленом
1, то неисправные модификации системы с примитивным многочленом 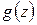
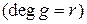 не будут обнаружены. Число примитивных многочленов равно:
не будут обнаружены. Число примитивных многочленов равно:
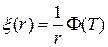 , (4.6)
, (4.6)
где 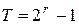 ;
; 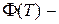 функция Эйлера, которая может быть выражена через функцию Мёбиуса следующим образом:
функция Эйлера, которая может быть выражена через функцию Мёбиуса следующим образом:
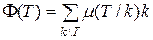 .
.
В этом случае для выражения (4.6) имеет вид :
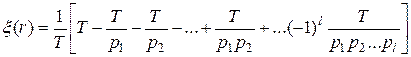 , (4.7)
, (4.7)
где 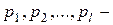 простые делители числа
простые делители числа 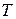 . Оценка ( 4.6) обычно для выражения (4.7) оказывается выше, чем для выражения (4.5).
. Оценка ( 4.6) обычно для выражения (4.7) оказывается выше, чем для выражения (4.5).
Оба способа определения достоверности кольцевого тестирования дают примерно одинаковые результаты.
Если 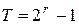 - простое число, то неравенство 4.5 для обоих случаев анализа результатов превращается в равенство:
- простое число, то неравенство 4.5 для обоих случаев анализа результатов превращается в равенство:
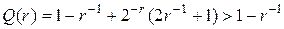 .
.
Это выражение является нижней границей определения достоверности кольцевого тестирования.
Верхней границей определения достоверности КТ является выражение:
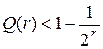 .
.
Таким образом, достоверность КТ лежит в пределах:
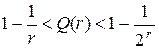 .
.
Определим далее достоверность тестирования во множестве неисправных модификаций ЛПОС. Пусть проверяемая ЛПОС преобразована в автономную ЛПОС (АЛПОС) введением обратной связи, так что уравнение переходов состояний АЛПОС имеет вид:
 ,
,
где 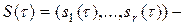 вектор-столбец состояний АЛПОС;
вектор-столбец состояний АЛПОС; 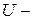 характеристическая матрица над
характеристическая матрица над 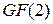 , имеющая размер
, имеющая размер  . Дополнительное оборудование, необходимое в тестовом режиме, состоит из дополнительных входов и выходов ЛПОС, используемых только в тестовом режиме, а также дополнительной ЛПОС, включаемой в контур обратной связи проверяемой ЛПОС. Под неисправностью проверяемой ЛПОС будем понимать физический дефект, приводящий к искажению матрицы
. Дополнительное оборудование, необходимое в тестовом режиме, состоит из дополнительных входов и выходов ЛПОС, используемых только в тестовом режиме, а также дополнительной ЛПОС, включаемой в контур обратной связи проверяемой ЛПОС. Под неисправностью проверяемой ЛПОС будем понимать физический дефект, приводящий к искажению матрицы 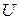 АЛПОС. Зададим неисправности в виде множества искажённых матриц
АЛПОС. Зададим неисправности в виде множества искажённых матриц 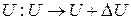 , где
, где 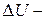 матрица размера
матрица размера 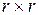 . Так как достоверность определяется по формуле 1.1, где
. Так как достоверность определяется по формуле 1.1, где 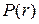 вероятность необнаружения искажения
вероятность необнаружения искажения 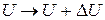 матрицы
матрицы 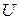 при условии равновероятности всех искажений.
при условии равновероятности всех искажений.
Таким образом, мощность множества 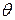 оказывается равной числу
оказывается равной числу 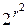 различных матриц
различных матриц 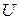 . Рассмотрим систему простого максимального периода
. Рассмотрим систему простого максимального периода 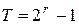 . В этом случае каждый примитивный многочлен
. В этом случае каждый примитивный многочлен 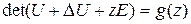 представляет один из классов
представляет один из классов 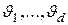 , имеющих одинаковые мощности:
, имеющих одинаковые мощности:
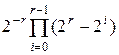 . (4.8)
. (4.8)
Имеет место теорема.
Теорема. Пусть характеристический многочлен АЛПОС является неприводимым многочленом степени 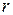 простого периода
простого периода 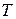 . Тогда достоверность кольцевого тестирования:
. Тогда достоверность кольцевого тестирования:
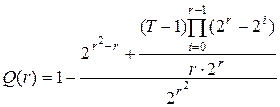 . (4.9)
. (4.9)
Формула (6.15) для достоверности 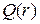 допускает нижнюю и верхнюю оценки. Так как
допускает нижнюю и верхнюю оценки. Так как 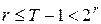 , а
, а 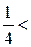
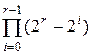
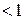 , тогда получаем:
, тогда получаем:
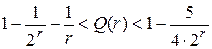 . (4.10)
. (4.10)
Причём это выполняется даже если максимальный период не является простым числом.
Дата добавления: 2016-03-15; просмотров: 1246;
