Достоверность КТ для произвольного периода.
Недостатком определения достоверности КТ в предыдущем разделе является невозможность определения достоверности при произвольном периоде 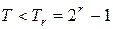 при фиксированном значении
при фиксированном значении 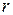 [1]. Как оказывается на практике, снижение периода
[1]. Как оказывается на практике, снижение периода 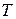 значительно снижает время на проведение теста (время уменьшается в
значительно снижает время на проведение теста (время уменьшается в 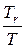 раз), но при этом возникает вопрос о том, как изменяется достоверность КТ. То есть задача состоит в том, чтобы определить достоверность КТ
раз), но при этом возникает вопрос о том, как изменяется достоверность КТ. То есть задача состоит в том, чтобы определить достоверность КТ 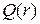 как функцию периода
как функцию периода 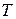 :
:
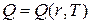 .
.
Очевидным фактом является то, что с понижением периода 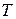 достоверность КТ должна уменьшаться.
достоверность КТ должна уменьшаться.
Для начала определим верхнюю границу достоверности для произвольного периода, а саму достоверность определим как функцию:
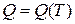 .
.
Чтобы определить значение верхней границы воспользуемся правой частью неравенства (6.13):
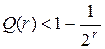 .
.
Значение правой части этого неравенства является частным случаем для максимального периода 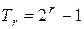 . Более того, эта формула не показывает зависимости достоверности
. Более того, эта формула не показывает зависимости достоверности 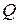 от периода
от периода 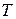 . Если установить зависимость достоверности
. Если установить зависимость достоверности 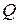 от максимального периода
от максимального периода 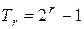 , тогда это будет справедливо для произвольного периода. Найдем эту зависимость:
, тогда это будет справедливо для произвольного периода. Найдем эту зависимость:
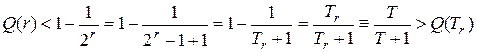 .
.
Тогда достоверность для произвольного периода определиться как:
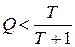 . (4.11) Если период
. (4.11) Если период 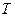 является простым числом, то можно преобразовать формулу (4.9) используя вышеприведённые рассуждения. Тогда получим:
является простым числом, то можно преобразовать формулу (4.9) используя вышеприведённые рассуждения. Тогда получим:
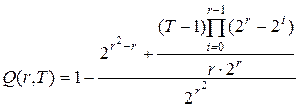 =
=
= 
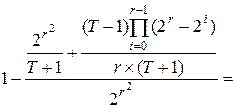
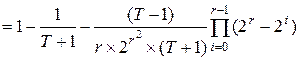 .
.
При больших значениях периода 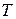 отношение
отношение 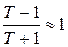 , тогда формула для определения достоверности произвольного (не обязательно максимального
, тогда формула для определения достоверности произвольного (не обязательно максимального 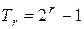 ) простого периода примет вид:
) простого периода примет вид:
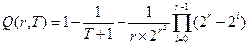 . (4.12)
. (4.12)
Верхние и нижние оценки достоверности КТ для формулы 1.10, приведённые по формуле (4.10), выполняются для произвольного максимального периода 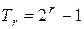 . Обобщим их для произвольного периода.
. Обобщим их для произвольного периода.
Нижняя оценка примет вид:
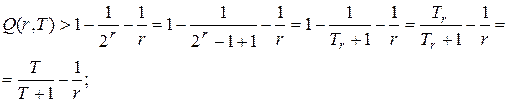
Верхняя граница примет вид:
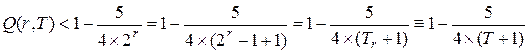 .
.
Итак, для произвольного не обязательно максимального периода получаем оценку достоверности КТ:
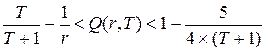 . (4.13)
. (4.13)
Таким образом, формула (4.10) является частным случаем формулы (4.13), когда период T является максимальным для данного значения r, то есть равен 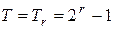 .
.
Дата добавления: 2016-03-15; просмотров: 1175;
