Лекция № 20. Плоскорадиальный фильтрационный поток упругой жидкости

Пусть в неограниченном горизонтальном пласте постоянной толщины h имеется скважина нулевого радиуса (точечный сток). В момент времени t = 0 скважина пущена в эксплуатацию с постоянным дебитом .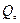

Распределение давления в пласте Р(r,t) определяется интегрированием уравнения (3), которое для плоскорадиального движения запишется в виде

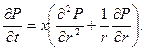(11)

Начальные и граничные условия таковы:

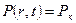при t=0

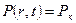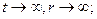при (12)

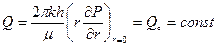при r=0, t >0.

Точное решение уравнения (11) при условиях (12) имеет вид:

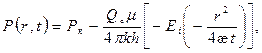(13)

где 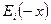- интегральная показательная функция.

Формула (13) получила название основной формулы теории упругого режима фильтрации.

При малых значениях 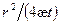интегральная показательная функция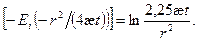

Тогда изменение давления на стенке скважины, определенное из (13) при 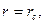будет:

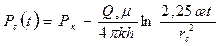(14)

Если в полубесконечном пласте работает n скважин, снижение давления в любой точке пласта М определяется с помощью метода суперпозиции по формуле:

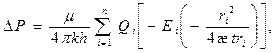(15)

где 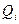– дебит i – ой скважины (при этом дебит добывающей скважины считается положительным, дебит нагнетательной – отрицательным; 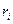- расстояние от центра i – ой скважины до точки М; 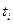- время с начала работы i – ой скважины до момента времени t, в которой определяется понижение давления.

Основная литература: 2 [133-150]

Дополнительная литература: 4 [277-283]

Контрольные вопросы:

1. Коэффициент пьезопроводности.

2. Основная формула теории упругого режима.

3. Интерференция скважин при упругом режиме.

4. Изменение давления на стенке скважины.