Лекция № 21,22. Приближенные методы решения задач теории упругого режима
1. Метод ПССС.
Плоско-параллельный поток.
А. В момент времени t=0 в горизонтальном пласте постоянной толщины h и ширины B пущена в эксплуатацию галерея с постоянным забойным давлением. До пуска галереи во всем пласте 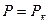 .
.
Требуется найти распределение давления, закон перемещения границы возмущенной области l(t) и изменение дебита галереи во времени Q(t).
Дебит галереи при установившемся процессе
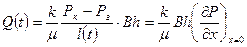 (1)
(1)
Воспользуемся уравнением материального баланса
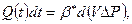 (2)
(2)
где 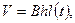
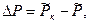
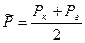 , (3)
, (3)
Подставляя (1) в (2) с учетом (3), получим
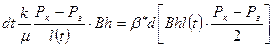
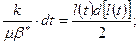
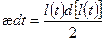 (4)
(4)
После интегрирования (4) будем иметь:
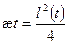 или
или 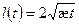 (5)
(5)
Распределение давления в возмущенной зоне
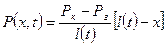 (6)
(6)
с учетом (5) имеем
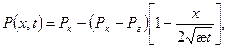
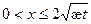 (7)
(7)
Дебит галереи 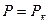 ,
, 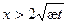
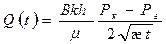 (8)
(8)
Погрешность не превосходит 11%
B, в том же пласте, как и в случае А, пущена галерея с постоянным дебитом.
В этом случае уравнения (2) с учетом (1) принимает вид:
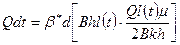 (9)
(9)
или 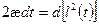
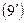
интегрируя 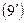 , получим,
, получим, 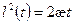 откуда
откуда 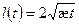 (10)
(10)
Распределение давления из (6) с учетом (1)
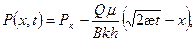
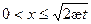 ,
,
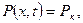
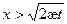 (11)
(11)
значение 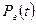 определяется из (11) при х=
определяется из (11) при х=
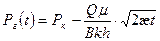 (12)
(12)
погрешность до 25%.
Плоскорадиальный поток
Пусть в неограниченном горизонтальном пласте постоянной толщины h в момент времени t=0, пущена добывающая скважина радиуса r 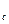 с постоянным дебитом Q. До пуска скважины во всем пласте
с постоянным дебитом Q. До пуска скважины во всем пласте 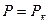 .
.
Через время t после пуска скважины вокруг нее образуется возмущенная область радиуса r где давление в соответствии с ПССС будет распределяться по стационарному закону
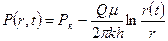 (13)
(13)
Дебит скважины
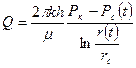 (14)
(14)
Размеры возмущенной области
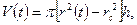 (15)
(15)
Т. к. 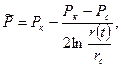 то
то 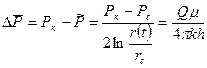 (16)
(16)
Подставив (15) и (16) в уравнение материального баланса (2), получим
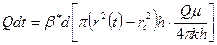
или 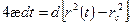
откуда 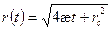 (17)
(17)
Подставляя (17) в (13), будем иметь
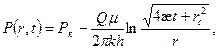
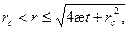
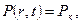
 (18)
(18)
Давление на скважине определяют из (8) при r=rc:
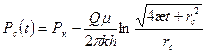 (19)
(19)
погрешность 10%.
2. Метод А. М. Пирвердяна.
В отличие от ПССС распределение давления в возмущенной области по методу А.М. Пирвердяна задается в виде квадратной параболы.
Рассматривается плоско-параллельный неустановившийся поток упругой жидкости.
А. Рассмотрим случай постоянного дебита Q=const.
Уравнение распределения давления в возмущенной области
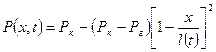 (20)
(20)
Дебит галереи
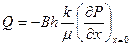 (21)
(21)
Градиент давления из (20)
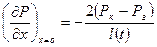
тогда (22)
Средневзвешенное по объему пластовое давление
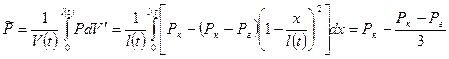
тогда 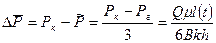 (23)
(23)
Уравнение материального баланса примет вид: 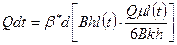
откуда 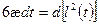 (24)
(24)
Интегрируя (24) в пределах от 0 до t и от 0 до l получим
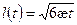 (25)
(25)
Распределение давления в возмущенной области
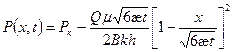 , 0 < x
, 0 < x 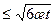 ,
,
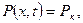
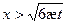
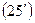
Давление на галерее определяется при
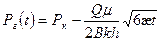 (26)
(26)
погрешность 9%, т. е. в 2,5 раза меньше, чем при
B. Рассмотрим случай, когда 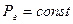 .
.
Уравнение материального баланса в этом случае принимает вид (с учетом (22) и (23))
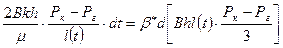
или 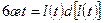 откуда
откуда 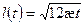 (27)
(27)
Распределение давления в возмущенной области:
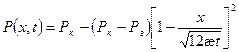 (28)
(28)
Дебит галереи 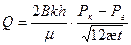 (29) погрешность около 2,5 %.
(29) погрешность около 2,5 %.
Основная литература: 2 [151-162]
Контрольные вопросы:
1. Сущность метода ПССС.
2. Закон перемещения внешней границы возмущенной области при постоянном дебите.
3. Закон перемещения внешней границы возмущенной области при Рг = const.
4. Сущность метода А.М. Пирвердяна.
5. Закон перемещения внешней границы возмущенной области по методу А.М. Пирвердяна.
Дата добавления: 2016-03-10; просмотров: 1391;
