Лекция № 25. Приближенное решение задач об отборе газа из замкнутого пласта.

Пусть в центре замкнутой круговой залежи радиуса 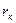находится скважина радиуса 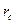. Начальное пластовое давление равно .

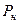Рассматриваются два случая:

а) отбор производится с постоянным дебитом ;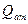

б) забойное давление сохраняется постоянным.

Обе задачи решаются методом ПССС, т.е. с использованием законов стационарной фильтрации газа и уравнения истощения залежи. Это последнее уравнение – уравнение материального баланса – заключается в том, что количество газа, извлеченного из пласта за некоторый промежуток времени, равно уменьшению запасов газа в пласте, так кА пласт ограничен, то запасы ограничены и не пополняются извне.

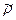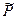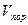Если - плотность идеального газа, соответствующая средневзвешенному давлению в пласте , а - объем порового пространства пласта, принимаемый постоянным, то уменьшение запасов газа за бесконечно малый промежуток времени запишется в виде:

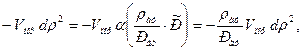(1)

отобранная масса газа за тот же промежуток времени 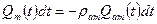(2)

Приравнивая (1) и (2), получим дифференциальное уравнение истощения газовой залежи:

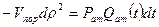(3)

Для установившейся плоскорадиальной фильтрации газа 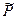очень мало отличается от давления на границе замкнутого пласта .

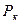Поэтому принимая 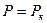, получим

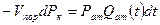(4)

Рассмотрим случай а) когда .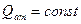

При этом 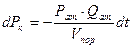(5)

Интегрируя (5), учитывая, что 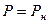при t=0, получаем

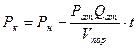(6)

Из формулы дебита скважины 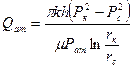(7)

можно выразить забойное давление: 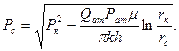(8)

С учетом (6) находим

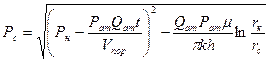(9)

В случае б) 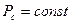для определения зависимости 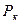от t подставим (7) в (4) и разделим переменные:

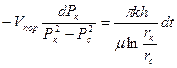(10)

Интегрируя (10) от 0 до t и от 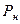до 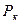, получим

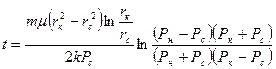(11)

Основная литература: 2 [185-186]

Дополнительная литература: 4 [306-315]

Контрольные вопросы:

1. Уравнение материального запаса.

2. Изменение запасов газа.

3. Забойное давление при постоянном дебите.

4. Изменение давления на верхней границе пласта при постоянном забойном давлении.