Системы массового обслуживания.
Ожидание того или иного вида обслуживания является частью нашей повседневной жизни. Мы ожидаем, чтобы пообедать в столовой, мы стоим в очереди к кассам в продовольственных магазинах и выстраиваемся в очередь для поездки в транспорте. Однако феномен ожидания характерен не только для людей: детали, поставленные в очередь для обработки на станке; группа пассажирских самолетов, ожидающих разрешения на посадку в аэропорту; автомобили, движение которых приостановлено сигналом светофора на пути их следования и т.п. К сожалению, феномен ожидания нельзя исключить без чрезмерных расходов. И лишь на одно мы можем надеяться — на возможность сокращения времени нежелательного ожидания в очереди до некоторых терпимых пределов.
7.1. Основные компоненты моделей массового обслуживания.
Основными элементами модели массового обслуживания являются клиент (заявка или требование на обслуживание либо просто "объект обслуживания") и сервис (обслуживающее устройство, средства обслуживания и т.п.). Клиенты поступают в систему обслуживания из источника. Поступив в сервис, они могут сразу же попасть на обслуживание или ожидать в очереди, если сервис занят. После завершения процедуры обслуживания сервис автоматически "выбирает" из очереди (если она имеется) одного из клиентов с тем, чтобы приступить к его обслуживанию. Если же очередь отсутствует, то сервис становится незанятым до прибытия нового клиента.
Поступление клиентов в систему обслуживания характеризуется интервалом между их последовательными поступлениями, а обслуживание – временем обслуживания клиента.
В анализе систем обслуживания определенную роль играет длина очереди, которая может быть как конечной, так и бесконечной. Изучение очередей в системах массового обслуживания позволяет определить критерии функционирования обслуживающей системы, среди которых наиболее значимыми являются среднее время ожидания в очереди и средняя длина очереди.
Важным фактором при анализе систем обслуживания является дисциплина очереди, определяющая порядок, в соответствии с которым выбираются клиенты из очереди для обслуживания. Наиболее распространенный принцип построения очереди основан на правиле "первым пришел – первым обслуживаешься" (это правило часто обозначается аббревиатурой FIFO – от английского First-In-First-Out).
Среди других правил, определяющих принципы построения очередей, укажем правило: "последним пришел – первым обслуживаешься" (обычно обозначается как LIFO — от английского Last-In-First-Out) и дисциплину очереди, определяемую случайным правилом отбора клиентов (иногда обозначается как SIRO – от английского Service-In-Random-Out). Кроме того, клиенты могут выбираться из очереди в соответствии с заданным приоритетом. Например, в производственном цехе срочные работы выполняются раньше обычных.
При анализе систем с очередями важным фактором является также поведение индивидуума, нуждающегося в обслуживании. Такие индивидуумы, выступающие в роли клиентов, при наличии параллельного обслуживания могут перейти из одной очереди в другую в надежде сократить продолжительность своего вынужденного ожидания. Они могут также отказаться от ожидания в очереди, так как люди обычно не переносят длительного бездействия, или покинуть очередь, простояв в ней какое-то время и придя к выводу, что и так уж слишком много времени потеряно.
Структура обслуживающей системы может включать один сервис или несколько таких средств обслуживания, работающих параллельно. Кроме того, сервисы могут быть расположены последовательно (например, обслуживание представляет собой комплекс работ, которые выполняются последовательно на различных станках).
Источник, генерирующий "клиентов", подлежащих обслуживанию, может иметь конечную или бесконечную мощность. Источник конечной мощности ограничивает число клиентов, поступающих на обслуживание (например, в цехе, располагающем 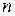 станками, суммарное количество потенциальных заявок на их ремонт не превышает
станками, суммарное количество потенциальных заявок на их ремонт не превышает 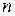 ). Наоборот, источник бесконечной мощности всегда имеет клиентов в "изобилии" (например, звонки, поступающие на телефонную станцию).
). Наоборот, источник бесконечной мощности всегда имеет клиентов в "изобилии" (например, звонки, поступающие на телефонную станцию).
Можно построить множество моделей систем массового обслуживания, варьируя перечисленные выше операционные характеристики систем. Далее рассматривается ряд таких моделей.
Результаты исследования системы обслуживания также можно использовать для оптимизации модели со стоимостными характеристиками, в которой минимизируется сумма затрат, связанных с предоставлением услуг, и потерь, обусловленных задержками в их предоставлении. На рис. 11 изображена типичная стоимостная модель системы обслуживания (в денежных единицах за единицу времени), где затраты на обслуживание возрастают с ростом его уровня. В то же время потери, обусловленные задержками в предоставлении услуг, уменьшаются с возрастанием уровня обслуживания. Главной проблемой, связанной с применением стоимостных моделей, является трудность оценки потерь в единицу времени, обусловленных задержками в предоставлении услуг. В частности, это особенно ощутимо, когда услуги предоставляются индивидууму, чье поведение может не совпадать с интересами функционирования системы обслуживания.
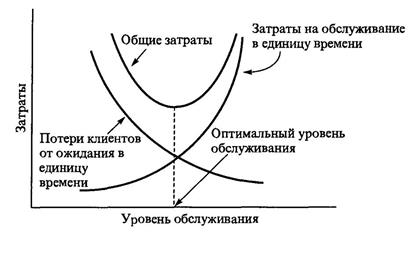
Рис. 11 Стоимостная модель системы обслуживания.
7.2. Экспоненциальное распределение в системах
массового обслуживания.
В большинстве систем массового обслуживания поступление заявок на обслуживание происходит случайным образом. Это означает, что наступление события (например, поступление клиента или завершение обслуживания) не зависит от времени, прошедшего с момента наступления предыдущего события.
Время между последовательными поступлениями клиентов и время их обслуживания, будучи случайными, при моделировании систем массового обслуживания количественно описываются экспоненциальным распределением, плотность вероятности которого имеет вид
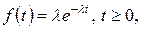
| (7.1) |
где математическое ожидание 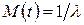 . То, что экспоненциальное распределение является совершенно случайным, иллюстрируется следующим примером.
. То, что экспоненциальное распределение является совершенно случайным, иллюстрируется следующим примером.
Если сейчас 8:20 и некое событие имело место в 8:02, то в соответствии с экспоненциальным законом распределения вероятность того, что следующее аналогичное событие произойдет в 8:29, является функцией лишь интервала времени от 8:20 до 8:29 и не зависит от интервала времени, прошедшего с момента наступления последнего события (от 8:02 до 8:20).
Данное свойство экспоненциального распределения обычно называют отсутствием последействия или отсутствием памяти. Докажем это утверждение.
Пусть время 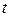 наступления какого-либо события распределено по экспоненциальному закону с функцией плотности
наступления какого-либо события распределено по экспоненциальному закону с функцией плотности 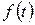 . Если
. Если 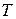 – время, прошедшее с момента наступления предыдущего события в момент времени
– время, прошедшее с момента наступления предыдущего события в момент времени 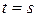 , то свойство отсутствия последействия выражается соотношением
, то свойство отсутствия последействия выражается соотношением
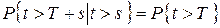
| (7.2) |
Для доказательства этого равенства заметим, что
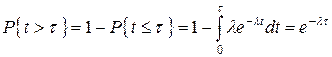
| (7.3) |
Следовательно
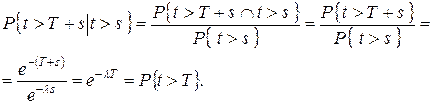
| (7.4) |
Пример. При обслуживании сложного агрегата всегда существует запасной блок для немедленной замены в случае поломки. Время выхода из строя агрегата (или его запасного блока) является случайной величиной, распределенной по экспоненциальному закону, и в среднем происходит каждые 40 минут. Оператор, обслуживающий агрегат, утверждает, что агрегат "имеет привычку" выходить из строя каждый вечер около 20:30. Проанализируем утверждение оператора.
Решение. Средняя интенсивность отказов агрегата равна 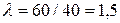 отказа в час. Следовательно, плотность экспоненциального распределения времени отказа имеет вид
отказа в час. Следовательно, плотность экспоненциального распределения времени отказа имеет вид
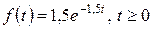 . .
| (7.5) |
Что касается заявления оператора, то и без вычислений видно, что оно не может соответствовать действительности, так как не согласуется с тем, что время между отказами агрегата распределено по экспоненциальному закону и, следовательно, является случайным. Для подтверждения или опровержения заявления оператора нельзя использовать вероятность того, что отказ будет происходить в 20:30, так как вероятность такого события зависит от времени дня (относительно 20:30), когда эта вероятность вычисляется. Например, если вычисления выполняются в 20:20, то вероятность того, что утверждение оператора окажется справедливым этим вечером, равна
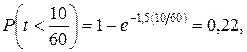
| (7.6) |
т.е. является очень малой. Если вычисления выполняются в 19:00, то вероятность того, что отказ будет иметь место в 20:30, возрастает примерно до 0,9 (проверьте!).
Эти два крайних значения вероятности показывают, что достоверность утверждения оператора нельзя проанализировать на основе полученных вероятностей; в данной ситуации мы должны полагаться только на характеристики экспоненциального распределения (точнее, на его свойство отсутствия последействия). ■
7.3. Модели рождения и гибели. Связь между экспоненциальным и Пуассоновским распределениями.
В данном разделе рассматриваются две составляющие обслуживающих систем. Первая представляет входной поток требований (модель чистого рождения). Вторая — непосредственно обслуживающее устройство, в которой описывается выход клиентов из системы (модель чистой гибели). Примером модели чистого рождения является процесс оформления свидетельств о рождении детей. В качестве модели чистой гибели может служить случайное изъятие хранящихся на складе запасов.
Обе модели строятся на основе экспоненциального распределения, которое задает интервал времени между рождениями или гибелью. Побочным продуктом этих построений является демонстрация тесной связи между экспоненциальным распределением и распределением Пуассона в том смысле, что одно из них автоматически определяет другое.
7.3.1. Модель чистого рождения.
Пусть 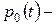 вероятность отсутствия событий (поступления клиентов) за период времени
вероятность отсутствия событий (поступления клиентов) за период времени 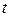 . При условии, что длина интервала времени
. При условии, что длина интервала времени 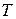 между поступлениями клиентов описывается экспоненциальным распределением с интенсивностью
между поступлениями клиентов описывается экспоненциальным распределением с интенсивностью 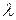 , будем иметь
, будем иметь
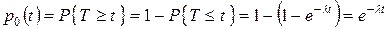 . .
| (7.7) |
При достаточно малом интервале времени  имеем
имеем
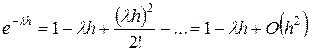 . .
| (7.8) |
Экспоненциальное распределение базируется на предположении, что на достаточно малом временном интервале  может наступить не более одного события (поступления клиента). Следовательно, при
может наступить не более одного события (поступления клиента). Следовательно, при 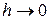
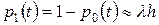 . .
| (7.9) |
Этот результат показывает, что вероятность поступления клиента на протяжении интервала 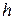 прямо пропорциональна
прямо пропорциональна 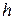 с коэффициентом пропорциональности, равным интенсивности поступлений
с коэффициентом пропорциональности, равным интенсивности поступлений 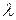 .
.
Чтобы получить распределение числа клиентов, поступивших на протяжении некоторого интервала времени, обозначим через 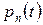 вероятность поступления
вероятность поступления 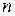 клиентов на протяжении времени
клиентов на протяжении времени 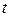 . При достаточно малом
. При достаточно малом  имеем следующее соотношение
имеем следующее соотношение
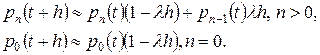
| (7.10) |
Из первого уравнения следует, что поступление 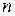 клиентов на протяжении времени
клиентов на протяжении времени 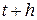 возможно в двух случаях: если имеется
возможно в двух случаях: если имеется 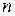 поступлений на протяжении времени
поступлений на протяжении времени 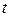 и нет поступлений за время
и нет поступлений за время 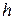 , или существует
, или существует 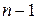 поступлений за время
поступлений за время 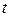 и одно поступление за время
и одно поступление за время 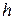 . Любые другие комбинации невозможны вследствие того, что на протяжении малого периода
. Любые другие комбинации невозможны вследствие того, что на протяжении малого периода 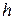 возможно наступление только одного события. В правой части уравнения, по сути дела, написана формула полной вероятности. Во втором уравнении отсутствие поступлений клиентов на протяжении интервала
возможно наступление только одного события. В правой части уравнения, по сути дела, написана формула полной вероятности. Во втором уравнении отсутствие поступлений клиентов на протяжении интервала 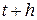 возможно лишь тогда, когда нет поступлений клиентов за время
возможно лишь тогда, когда нет поступлений клиентов за время 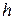 .
.
Перегруппировывая члены и переходя к пределу при 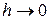 , получаем
, получаем
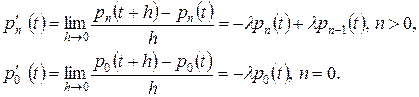
| (7.11) |
где 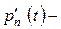 производная по
производная по 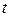 функции
функции 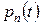 .
.
Решение приведенных выше разностно-дифференциальных уравнений имеет следующий вид:
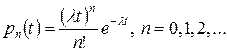 . .
| (7.12) |
В данном случае мы получили дискретную плотность вероятности распределения Пуассона с математическим ожиданием 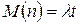 поступлений за время
поступлений за время 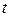 . Дисперсия распределения Пуассона также равна
. Дисперсия распределения Пуассона также равна 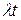 .
.
Полученный результат означает, что всякий раз, когда временные интервалы между моментами последовательных поступлений заявок распределены по экcпоненциальному закону с математическим ожиданием 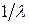 , число поступлений заявок в интервале, равном
, число поступлений заявок в интервале, равном 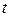 единиц времени, характеризуется распределением Пуассона с математическим ожиданием
единиц времени, характеризуется распределением Пуассона с математическим ожиданием 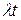 . Верным является и обратное утверждение.
. Верным является и обратное утверждение.
Соответствие между экспоненциальным распределением (с интенсивностью поступлений 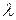 ) и распределением Пуассона показано в таблице 34.
) и распределением Пуассона показано в таблице 34.
Таблица 34.
| Экспоненциальное распределение | Распределение Пуассона | |
| Случайная переменная | Время 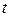 между
наступлениями событий между
наступлениями событий
| Количество 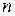 поступлений событий в течение
периода времени поступлений событий в течение
периода времени 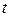
|
| Значение случайной величины | 
| 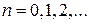
|
| Функция плотности вероятности | 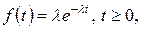
| 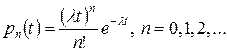
|
| Среднее значение (математическое ожидание) | 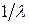 временных единиц временных единиц
| 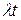 поступлений за время поступлений за время 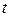
|
| Функция распределения | 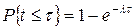
| 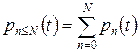
|
Вероятность, что не произойдет ни
одного события в течение времени 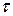
| 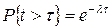
|
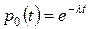
|
Пример. В автосервис каждые 12 минут подъезжает на ремонт автомобиль. Время между прибытиями автомобилей распределено по экспоненциальному закону. Требуется определить следующее:
1. Среднее число обратившихся на автосервис за год.
2. Вероятность того, что на протяжении одного дня не подъедет ни одного автомобиля.
3. Вероятность постановки на ремонт 50 автомобилей к концу третьего часа, если известно, что на протяжении последних двух часов было уже поставлено на ремонт 40 автомобилей.
Решение. Вычислим интенсивность поступления автомобилей на ремонт за день: 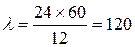 автомобилей за сутки.
автомобилей за сутки.
1. Интенсивность ремонтных работ за год равна 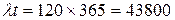 ремонтов.
ремонтов.
2. Вероятность того, что на протяжении одного дня не прибудет ни одна автомашина на ремонт, вычисляется с использованием пуассоновского распределения
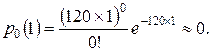
|
3. Для вычисления вероятности постановки на ремонт 50 автомобилей к концу третьего часа при условии, что на протяжении последних двух часов было уже поставлено на ремонт 40 автомобилей, заметим, что, поскольку распределение числа обратившихся за ремонтом автомобилей является пуассоновским, искомая вероятность сводится к вероятности появления 10 (= 50 - 40) автомобилей за один (=3-2) час. Так как 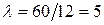 автомобилей за час, то
автомобилей за час, то
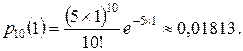 ■ ■
|
7.3.2. Модель чистой гибели.
Мы исходим из предположения, что каждый прибор (или канал) обслуживания может в одно и то же время обслуживать только одно требование. Допустим, что для каждого рассматриваемого прибора длительности следующих один за другим интервалов обслуживания распределены независимым и идентичным образом и могут быть описаны с помощью плотности распределения, представляющей собой непрерывную функцию.
Пусть 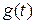 - плотность распределения вероятностей того, что в интервале продолжительности t будет обслужено одно требование t>0. Обозначим среднее время обслуживания
- плотность распределения вероятностей того, что в интервале продолжительности t будет обслужено одно требование t>0. Обозначим среднее время обслуживания  :
:
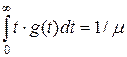 , ,
| (7.13) |
так что m - число требований, обслуженных за единицу времени. Так, например, если за 1 час, обслуживающий прибор успевает обслужить 5 требований, то среднее время обслуживания одного требования составляет 0,2 часа.
В большинстве случаев, считают, что распределение длительностей обслуживания является экспоненциальным:
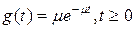 . .
| (7.14) |
При таком законе распределения случайной величины t вероятность завершения обслуживания клиента в любой последующий интервал времени не зависит (и это можно доказать) от того, сколько времени t уже потрачено на обслуживание данного требования, а зависит только от длительности интервала h.
Если в момент 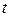 требование уже обслуживалось, и мы рассматриваем систему в момент времени
требование уже обслуживалось, и мы рассматриваем систему в момент времени 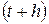 , то вероятность того, что на этом интервале обслуживание не заканчивается, определяется формулой
, то вероятность того, что на этом интервале обслуживание не заканчивается, определяется формулой
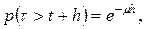
| (7.15) |
где t - время обслуживания. Будем считать, что h очень мало. Тогда можно предположить, что число событий, состоящих в выходе требования из системы, не может быть больше одного. Кроме того, так как 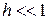 , то:
, то:
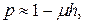
| (7.16) |
и вероятность завершения обслуживания в интервале 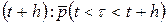 , теперь определяется как:
, теперь определяется как:
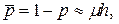
| (7.17) |
Рассмотрим следующую модель, которая называется моделью чистой гибели. Пусть система функционирует, начиная с момента 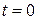 . В данной модели предполагается, что система начинает функционировать, когда в момент времени
. В данной модели предполагается, что система начинает функционировать, когда в момент времени 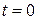 в ней имеется
в ней имеется  клиентов и не допускается ни одного нового поступления клиента. Обслуженные клиенты выбывают из системы с интенсивностью
клиентов и не допускается ни одного нового поступления клиента. Обслуженные клиенты выбывают из системы с интенсивностью 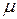 клиентов в единицу времени. Пусть
клиентов в единицу времени. Пусть 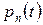 - вероятность того, что после
- вероятность того, что после 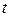 временных единиц в системе остается
временных единиц в системе остается 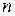 клиентов. Для получения разностно - дифференциальных уравнений относительно
клиентов. Для получения разностно - дифференциальных уравнений относительно 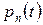 обычно следуют логике рассуждений, использованных в модели чистого рождения (раздел 7.3.1). Поэтому имеем
обычно следуют логике рассуждений, использованных в модели чистого рождения (раздел 7.3.1). Поэтому имеем
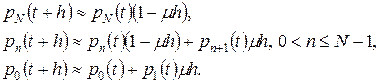
| (7.18) |
При 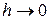 отсюда получим
отсюда получим
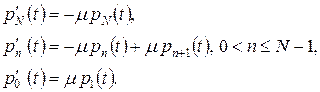
| (7.19) |
Эти уравнения имеют решение вида
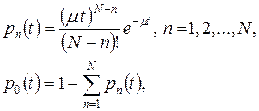
| (7.20) |
которое называется усеченным распределением Пуассона.
Пример.Ремонтный цех предприятия только что складировал 10 комплектов запасных частей для ремонта автомобилей данного предприятия. Пополнение запаса в таком же объеме происходит каждые 7 дней. Время между поломками автомобилей является случайной величиной, распределенной по экспоненциальному закону со средним значением, равным одному дню. Определите вероятность того, что автомобиль 2 дня будет находиться в неисправном состоянии из-за отсутствия запасных частей.
Так как комплекты запчастей требуются для ремонта с интенсивностью 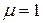 комплект в день, то вероятность того, что запчасти будут отсутствовать в конце дня с номером
комплект в день, то вероятность того, что запчасти будут отсутствовать в конце дня с номером 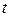 , определяется формулой
, определяется формулой
 . .
|
Чтобы автомобиль простоял два дня, запчасти должны закончиться в конце пятого дня. То есть искомая вероятность равна
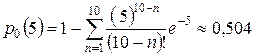 .■ .■
|
7.4. Общая модель системы массового обслуживания.
В данном разделе рассматриваются общие системы массового обслуживания, в которых есть как входной поток клиентов, так и выходной поток обслуженных клиентов. Время между последовательными поступлениями клиентов и время обслуживания являются экспоненциально распределенными случайными величинами.
При рассмотрении общих систем массового обслуживания предполагается, что система функционирует в течение достаточно большого интервала времени, по истечении которого в ее работе наступает стационарный режим.
В рассматриваемой в этом разделе общей модели системы массового обслуживания предполагается, что и интенсивность поступления клиентов, и интенсивность выходного потока зависят от состояния системы, что означает их зависимость от числа клиентов в системе обслуживания. Например, сборщик платы за проезд по автомагистрали в часы интенсивного движения стремится ускорить сбор пошлины. Или в мастерской с фиксированным количеством станков интенсивность их поломки убывает по мере возрастания числа аварийных станков, ибо лишь работающие станки могут выходить из строя.
Введем следующие обозначения:
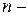 число клиентов в системе обслуживания (в очереди и на обслуживании),
число клиентов в системе обслуживания (в очереди и на обслуживании),
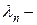 интенсивность поступления в систему клиентов при условии, что в системе уже находится
интенсивность поступления в систему клиентов при условии, что в системе уже находится 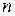 клиентов,
клиентов,
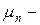 интенсивность выходного потока обслуженных клиентов при условии, что в системе находится
интенсивность выходного потока обслуженных клиентов при условии, что в системе находится 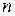 клиентов,
клиентов,
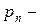 вероятность того, что в системе находится
вероятность того, что в системе находится 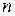 клиентов.
клиентов.
В общей модели системы массового обслуживания устанавливается функциональная зависимость вероятностей 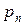 от
от 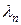 и
и  . Эти вероятности используются затем при определении функциональных характеристик обслуживающей системы, таких как средняя длина очереди, среднее время ожидания и средний коэффициент использования сервисов.
. Эти вероятности используются затем при определении функциональных характеристик обслуживающей системы, таких как средняя длина очереди, среднее время ожидания и средний коэффициент использования сервисов.
Как показано в разделе 7.2, вероятность появления более одного нового клиента на протяжении малого промежутка времени 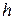 стремится к нулю при
стремится к нулю при 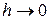 . Это означает, что при
. Это означает, что при 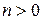 состояние
состояние 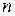 может быть изменено в двух возможных направлениях:
может быть изменено в двух возможных направлениях: 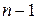 , когда с интенсивностью
, когда с интенсивностью 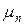 обслуженный клиент выбывает из системы, и
обслуженный клиент выбывает из системы, и 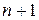 , когда клиенты поступают с интенсивностью
, когда клиенты поступают с интенсивностью 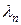 . Состояние 0 может измениться лишь к состоянию 1, когда имеет место поступление клиента с интенсивностью
. Состояние 0 может измениться лишь к состоянию 1, когда имеет место поступление клиента с интенсивностью 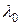 . Заметим, что
. Заметим, что 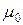 не определено, так как клиенты не могут выбывать из пустой системы обслуживания.
не определено, так как клиенты не могут выбывать из пустой системы обслуживания.
При выполнении условий стационарности ожидаемые интенсивности входного и выходного потоков в состоянии 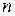
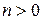 должны быть равны. Так состояние
должны быть равны. Так состояние 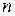 может изменяться лишь к состояниям
может изменяться лишь к состояниям 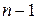 и
и 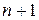 , отсюда следует
, отсюда следует
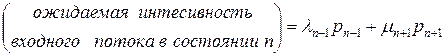 . .
| (7.10) |
Аналогично
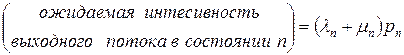 . .
| (7.11) |
Приравнивая эти две интенсивности, получаем следующее уравнение баланса
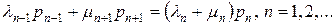 . .
| (7.12) |
При 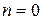 получаем
получаем
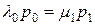 . .
| (7.13) |
Уравнения баланса решаются рекуррентно, последовательно выражая вероятности 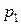 через
через 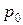 следующим образом: для
следующим образом: для 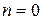 имеем
имеем
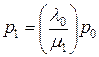 . .
| (7.14) |
Для 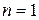 получаем
получаем
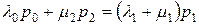 . .
| (7.15) |
Подставляя сюда (7/14) и упрощая полученное выражение, имеем (проверьте!)
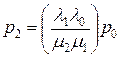 . .
| (7.16) |
Методом индукции можно показать, что
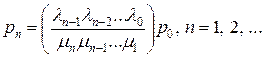 . .
| (7.17) |
Значение 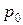 определяется из уравнения
определяется из уравнения  .
.
Пример. Бакалейный магазин работает с тремя кассами. Вывеска возле касс извещает покупателей, что в любой момент будет открыта дополнительная касса, как только число покупателей в любой очереди превысит 3. Это означает, что если число покупателей меньше четырех, то работать будет лишь одна касса. Если число покупателей от четырех до шести, то будет работать две кассы. Если имеется больше шести покупателей, будут открыты все три кассы. Покупатели подходят к кассам в соответствии с распределением Пуассона с математическим ожиданием 10 человек в час.
Время обслуживания одного покупателя в кассе распределено по экспоненциальному закону со средним 12 минут. Определим в установившемся режиме вероятность 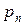 , что
, что 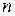 покупателей стоят в очереди в кассу.
покупателей стоят в очереди в кассу.
Решение. Из формулировки задачи имеем следующее:  покупателей в час независимо от
покупателей в час независимо от 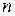 . Число обслуживаемых клиентов
. Число обслуживаемых клиентов
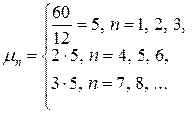 . .
| (7.18) |
Следовательно,
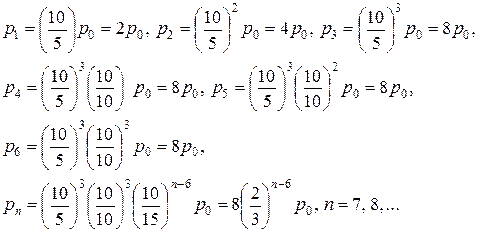 .
.
| (7.19) |
Значение 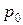 определяется из уравнения
определяется из уравнения
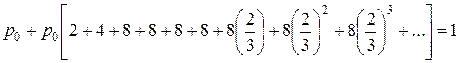
|
или, что равносильно,
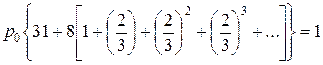 . .
|
В квадратных скобках стоит сумма бесконечной геометрической прогрессии, которая легко вычисляется. В результате имеем
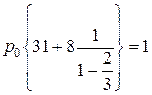 . .
|
Следовательно, 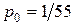 .
.
Зная 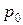 , можно определить любую вероятность, имеющую отношение к задаче. Например, вероятность того, что будет работать лишь одна касса, вычисляется как вероятность нахождения в системе не больше трех клиентов, т.е.
, можно определить любую вероятность, имеющую отношение к задаче. Например, вероятность того, что будет работать лишь одна касса, вычисляется как вероятность нахождения в системе не больше трех клиентов, т.е.
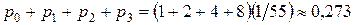 . .
|
Здесь предполагается, что в бакалейном магазине будет открыта как минимум одна касса, даже в том случае, когда вовсе нет покупателей.
Вероятности 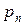 можно использовать для определения численных значений функциональных характеристик рассматриваемой системы. Например, среднее количество неработающих касс равно
можно использовать для определения численных значений функциональных характеристик рассматриваемой системы. Например, среднее количество неработающих касс равно
 касса. ■ касса. ■
|
7.5. Функциональные характеристики стационарных систем обслуживания.
Основными функциональными характеристиками систем массового обслуживания являются следующие:
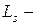 среднее число находящихся в системе клиентов,
среднее число находящихся в системе клиентов,
 среднее число клиентов в очереди,
среднее число клиентов в очереди,
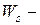 средняя продолжительность пребывания клиента в системе,
средняя продолжительность пребывания клиента в системе,
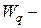 средняя продолжительность пребывания клиента в очереди,
средняя продолжительность пребывания клиента в очереди,
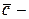 среднее количество занятых средств обслуживания (сервисов).
среднее количество занятых средств обслуживания (сервисов).
Напомним, что система включает как очередь, так и средства обслуживания.
Покажем, как перечисленные функциональные характеристики получаются из вероятностей 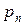 – вероятностей того, что в системе находится
– вероятностей того, что в системе находится 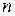 клиентов. В частности, имеем следующее.
клиентов. В частности, имеем следующее.
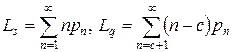 . .
| (7.20) |
Зависимость между 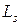 и
и 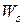 (а также между
(а также между 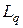 и
и 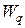 ), известная в литературе по теории массового обслуживания как формула Литтла, имеет вид
), известная в литературе по теории массового обслуживания как формула Литтла, имеет вид
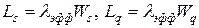 . .
|
Эти соотношения справедливы при достаточно общих условиях. Параметр 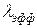 представляет собой эффективную интенсивность поступления клиентов в систему обслуживания. Он равен (исходной) интенсивности поступления клиентов
представляет собой эффективную интенсивность поступления клиентов в систему обслуживания. Он равен (исходной) интенсивности поступления клиентов 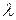 , когда все прибывающие клиенты имеют возможность попасть в обслуживающую систему. Если же некоторые клиенты не имеют такой возможности по той причине, что она заполнена (например, заполненная автостоянка), то
, когда все прибывающие клиенты имеют возможность попасть в обслуживающую систему. Если же некоторые клиенты не имеют такой возможности по той причине, что она заполнена (например, заполненная автостоянка), то 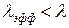 . Позже мы покажем, как вычисляется
. Позже мы покажем, как вычисляется 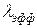 .
.
Существует также прямая зависимость между величинами  . По определению
. По определению
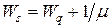 . .
| (7.21) |
Отсюда получим формулу, связывающую 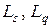 . Умножая обе части последнего соотношения на
. Умножая обе части последнего соотношения на 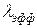 и используя формулу Литтла, в результате получаем
и используя формулу Литтла, в результате получаем
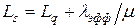 . .
| (7.22) |
По определению разность между средним числом находящихся в системе клиентов 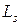 и средним числом клиентов в очереди
и средним числом клиентов в очереди 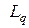 равна среднему количеству занятых узлов обслуживания
равна среднему количеству занятых узлов обслуживания 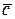 . Следовательно, имеем
. Следовательно, имеем
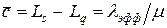 . .
| (7.23) |
Поэтому коэффициент использования узлов обслуживания вычисляется как отношение 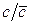 .
.
Пример. Автостоянка для посетителей колледжа имеет всего пять мест. Автомобили прибывают на стоянку в соответствии с распределением Пуассона с интенсивностью шесть автомобилей в час. Время пребывания автомобилей на стоянке является экспоненциально распределенной случайной величиной со средним 30 мин. Посетители, которые не могут найти свободного места на стоянке непосредственно по прибытии, могут временно ожидать освобождения места на территории стоянки. Таких мест для ожидания на стоянке имеется три. Если и стоянка, и все места для ожидания заполнены, то прибывшие автомобили вынуждены искать другую автостоянку. Требуется определить следующее:
а) вероятность 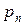 того, что в системе находится
того, что в системе находится 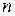 автомобилей,
автомобилей,
б) эффективную интенсивность поступления автомобилей на стоянку,
в) среднее количество автомобилей на стоянке,
г) среднее время нахождения автомобиля в очереди на территории стоянки,
д) среднее количество занятых мест на автостоянке.
Решение. Прежде всего, заметим, что место для стоянки в рассматриваемой ситуации выступает в роли сервиса, так что система имеет всего 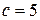 средств обслуживания. Максимальная вместимость системы равна 5 + 3 = 8 автомобилей.
средств обслуживания. Максимальная вместимость системы равна 5 + 3 = 8 автомобилей.
Вероятность 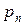 может быть определена как частный случай из общей модели, рассмотренной в разделе 7.4. Например, имеем
может быть определена как частный случай из общей модели, рассмотренной в разделе 7.4. Например, имеем
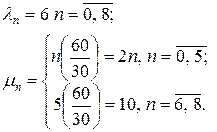 . .
|
Следовательно, из соотношений, полученных в разделе 7.4, вычисляем
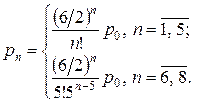 . .
|
Из условия 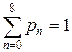 находим
находим 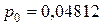 (проверьте!). Найденное значение
(проверьте!). Найденное значение
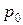 позволяет вычислить все вероятности от
позволяет вычислить все вероятности от 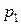 до
до 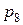 :
:
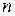
| ||||||||
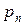
| 0,14436 | 0,21654 | 0,21654 | 0,16240 | 0,09744 | 0,05847 | 0,03508 | 0,02105 |
Найдем эффективную интенсивность поступления автомобилей на стоянку 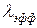 . Прибывающий автомобиль может поступить на стоянку с интенсивностью
. Прибывающий автомобиль может поступить на стоянку с интенсивностью 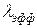 или уехать в поисках другой стоянки с интенсивностью
или уехать в поисках другой стоянки с интенсивностью 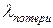 , т.е.
, т.е. 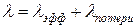 . Автомобиль не может въехать на стоянку, если там уже имеется 8 автомобилей. Это значит, что часть автомобилей, которые не смогут попасть на стоянку, пропорциональна
. Автомобиль не может въехать на стоянку, если там уже имеется 8 автомобилей. Это значит, что часть автомобилей, которые не смогут попасть на стоянку, пропорциональна 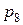 . Следовательно,
. Следовательно,
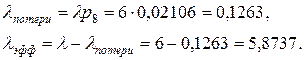
|
Среднее количество автомобилей на стоянке (тех, которые занимают места стоянки, и тех, которые ожидают места) определяется значением 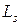 – средним числом клиентов в системе по формуле (7.20). В результате получаем
– средним числом клиентов в системе по формуле (7.20). В результате получаем 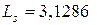 автомобилей.
автомобилей.
Автомобиль, ожидающий, пока освободится место для стоянки, фактически находится в очереди. Следовательно, время его ожидания равно величине 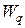 . Для вычисления
. Для вычисления 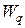 используем определение
используем определение
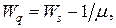 где
где 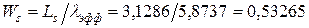 часа. Теперь
часа. Теперь 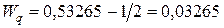 часа.
часа.
Среднее количество занятых мест на автостоянке равно среднему значению "занятых сервисов" и поэтому вычисляется следующим образом
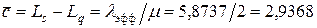 мест. Отсюда получаем, что коэффициент использования мест на стоянке равен
мест. Отсюда получаем, что коэффициент использования мест на стоянке равен 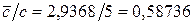 .■
.■
7.6. Модели с одним сервисом.
В этом разделе представлены две модели обслуживающей системы с одним средством обслуживания (т.е. 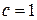 ). Предполагается, что клиенты поступают с постоянной интенсивностью
). Предполагается, что клиенты поступают с постоянной интенсивностью 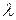 . Интенсивность обслуживания также постоянна и равна
. Интенсивность обслуживания также постоянна и равна 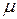 клиентов в единицу времени. Первая модель не устанавливает ограничений на вместимость системы, во второй модели предполагается, что вместимость системы является ограниченной. В этих двух моделях источник, "порождающий" клиентов, имеет неограниченную емкость.
клиентов в единицу времени. Первая модель не устанавливает ограничений на вместимость системы, во второй модели предполагается, что вместимость системы является ограниченной. В этих двух моделях источник, "порождающий" клиентов, имеет неограниченную емкость.
Используя обозначения общей модели, имеем 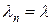 и
и 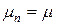 для всех
для всех 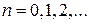 . Поскольку отсутствуют ограничения на емкость очереди, и, следовательно, все прибывающие клиенты могут попасть в систему обслуживания, то
. Поскольку отсутствуют ограничения на емкость очереди, и, следовательно, все прибывающие клиенты могут попасть в систему обслуживания, то 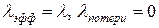 .
.
Обозначим 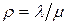 - трафик интенсивности. Тогда выражение для вероятности
- трафик интенсивности. Тогда выражение для вероятности 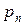 в общей модели принимает следующий вид:
в общей модели принимает следующий вид:
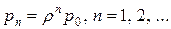 . .
| (7.24) |
Для определения величины 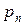 используется тождество
используется тождество
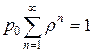 . .
| (7.25) |
Предполагаем, что 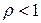 , тогда геометрический ряд имеет конечную сумму
, тогда геометрический ряд имеет конечную сумму 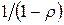 , поэтому
, поэтому 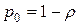 . Следовательно, общая формула для
. Следовательно, общая формула для 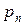 имеет вид
имеет вид
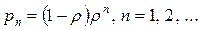 . .
| (7.26) |
Эти значения вероятностей 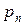 (включая вероятность
(включая вероятность 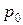 ) соответствуют геометрическому распределению.
) соответствуют геометрическому распределению.
Среднее число находящихся в системе клиентов 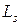 как функциональная характеристика обслуживающей системы вычисляется по следующей формуле:
как функциональная характеристика обслуживающей системы вычисляется по следующей формуле:
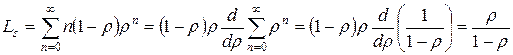 . .
| (7.27) |
Так как в рассматриваемой модели  , то остальные функциональные характеристики обслуживающей системы вычисляются с использованием соотношений из раздела 7.5, что приводит к следующим результатам:
, то остальные функциональные характеристики обслуживающей системы вычисляются с использованием соотношений из раздела 7.5, что приводит к следующим результатам:
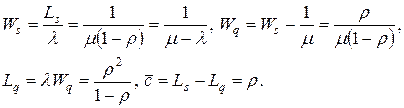 . .
| (7.28) |
Пример. Автоматическая мойка для автомобилей имеет только один моечный бокс. Автомобили прибывают в соответствии с распределением Пуассона со средним 4 машины в час и могут ожидать обслуживания на стоянке рядом с автомойкой. Время мойки автомобиля является экспоненциально распределенной случайной величиной с математическим ожиданием 10 мин. Автомобили, которые не помещаются на стоянке, могут ожидать на прилегающей к автомойке улице. Это значит, что практически нет ограничений на емкость системы обслуживания. Хозяин автомойки хочет определить количество мест на стоянке для автомобилей.
Решение. Для рассматриваемой задачи имеем 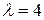 автомобиля в час,
автомобиля в час, 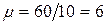 автомобилей в час,
автомобилей в час, 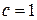 , емкость системы равна
, емкость системы равна 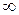 и емкость источника также равна
и емкость источника также равна 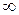 .
.
Из этих данных получаем, что среднее количество автомашин, ожидающих в очереди, равно 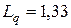 автомашины. Мы не можем рассматривать
автомашины. Мы не можем рассматривать 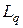 в качестве единственного аргумента при определении искомого количества мест на стоянке, ибо при расчете должна учитываться максимально возможная длина очереди. Например, можно рассчитать количество мест на стоянке, при котором, по меньшей мере, 90 % прибывших автомобилей найдет место на стоянке.
в качестве единственного аргумента при определении искомого количества мест на стоянке, ибо при расчете должна учитываться максимально возможная длина очереди. Например, можно рассчитать количество мест на стоянке, при котором, по меньшей мере, 90 % прибывших автомобилей найдет место на стоянке.
Пусть неизвестная переменная 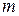 представляет искомое количество мест на стоянке. Тогда система имеет емкость
представляет искомое количество мест на стоянке. Тогда система имеет емкость 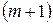 (очередь плюс место на мойке). Прибывающий автомобиль в 90 % случаев получит место на стоянке, если в системе находится максимум
(очередь плюс место на мойке). Прибывающий автомобиль в 90 % случаев получит место на стоянке, если в системе находится максимум 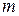 автомобилей. Это условие эквивалентно следующему вероятностному утверждению:
автомобилей. Это условие эквивалентно следующему вероятностному утверждению:
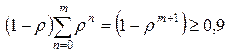 . .
|
Отсюда получаем 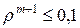 или
или 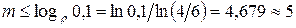 . Таким образом, необходимо
. Таким образом, необходимо 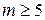 мест на стоянке. ■
мест на стоянке. ■
Обозначим через 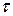 количество времени, которое только что прибывший клиент проведет в системе от момента прибытия до завершения обслуживания. Исходя из дисциплины очереди, первым пришел – первым обслужился, если в системе уже находится
количество времени, которое только что прибывший клиент проведет в системе от момента прибытия до завершения обслуживания. Исходя из дисциплины очереди, первым пришел – первым обслужился, если в системе уже находится 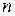 клиентов, которые поступили в систему перед только что прибывшим, то полное время пребывания требования в системе представляет собой сумму
клиентов, которые поступили в систему перед только что прибывшим, то полное время пребывания требования в системе представляет собой сумму 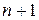 независимых выборок из множества значений, принимаемых случайной величиной
независимых выборок из множества значений, принимаемых случайной величиной 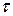 , каждая из которых подчиняется одному и тому же экспоненциальному распределению. Как известно из теории вероятностей, в этом случае функция
, каждая из которых подчиняется одному и тому же экспоненциальному распределению. Как известно из теории вероятностей, в этом случае функция 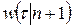 будет плотностью вероятности гамма-распределения с параметрами
будет плотностью вероятности гамма-распределения с параметрами 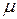 и
и 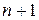 . Отсюда следует, что
. Отсюда следует, что
 . .
| (7.29) |
Таким образом, показано, что случайная величина 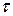 имеет экспоненциальное распределение с математическим ожиданием
имеет экспоненциальное распределение с математическим ожиданием 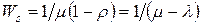 . Тогда время пребывания в очереди
. Тогда время пребывания в очереди 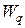 , очевидно, равно времени пребывания в системе за исключением времени обслуживания 1 / m. То есть:
, очевидно, равно времени пребывания в системе за исключением времени обслуживания 1 / m. То есть:
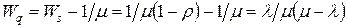 . .
| (7.30) |
Рассмотрим теперь случай, который отличается от рассмотренного выше только тем, что система вмещает не более  клиентов (максимальная длина очереди равняется
клиентов (максимальная длина очереди равняется 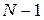 ). Примерами обслуживающей системы такого типа служат производственные ситуации, когда станок может иметь ограниченную зону складирования заготовок, а также рестораны быстрого питания с одним пунктом обслуживания клиентов на автомобилях и т.д.
). Примерами обслуживающей системы такого типа служат производственные ситуации, когда станок может иметь ограниченную зону складирования заготовок, а также рестораны быстрого питания с одним пунктом обслуживания клиентов на автомобилях и т.д.
Ситуация в рассматриваемой модели такова, что, как только число клиентов в системе достигает  , ни один из дополнительных клиентов на обслуживание не принимается. Из этого условия следует, что
, ни один из дополнительных клиентов на обслуживание не принимается. Из этого условия следует, что
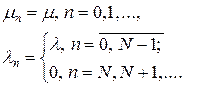 . .
| (7.31) |
Используя обозначение 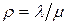 , имеем
, имеем
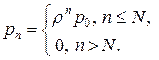 . .
| (7.32) |
Из равенства 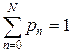 получаем
получаем 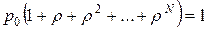 . Откуда
. Откуда
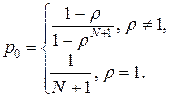 . .
| (7.33) |
Следовательно,
 . .
| (7.34) |
Заметим, что в этой модели значение параметра 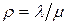 и не обязательно должно быть меньше единицы, так как поступления клиентов в систему контролируются максимальной емкостью системы
и не обязательно должно быть меньше единицы, так как поступления клиентов в систему контролируются максимальной емкостью системы  . Это значит, что в данном случае в качестве интенсивности поступления клиентов скорее выступает
. Это значит, что в данном случае в качестве интенсивности поступления клиентов скорее выступает 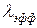 , нежели
, нежели 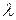 . Так как клиенты будут потеряны в том случае, если в системе находится
. Так как клиенты будут потеряны в том случае, если в системе находится  клиентов, то
клиентов, то
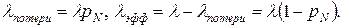 . .
| (7.35) |
Среднее число клиентов в системе вычисляется по формуле
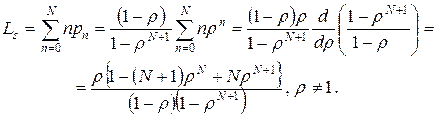 . .
| (7.36) |
При 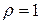
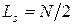 (проверьте!). Используя значения
(проверьте!). Используя значения 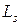 и
и 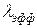 , можно также получить выражения для
, можно также получить выражения для 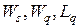 , как это сделано в подразделе 7.5.
, как это сделано в подразделе 7.5.
7.7. Модели с параллельными сервисами.
В этом разделе рассматриваются две модели систем массового обслуживания с несколькими параллельно работающими средствами обслуживания (сервисами). Эти модели представляют собой обобщение моделей, рассмотренных в подразделе 7.6., для ситуации нескольких параллельно работающих сервисов.
Первая модель предусматривает работу с параллельных средств обслуживания. Интенсивность входного потока клиентов равна 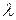 , а интенсивность обслуживания клиентов –
, а интенсивность обслуживания клиентов – 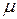 для каждого сервиса. Поскольку отсутствуют ограничения на количество клиентов в системе, то
для каждого сервиса. Поскольку отсутствуют ограничения на количество клиентов в системе, то  .
.
Результатом использования с параллельных сервисов является пропорциональное увеличение интенсивности обслуживания клиентов системой до 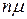 , если
, если 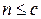 , и до
, и до 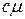 , если
, если 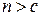 . Следовательно, в терминах общей модели системы обслуживания
. Следовательно, в терминах общей модели системы обслуживания 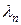 и
и 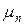 определяются следующим образом:
определяются следующим образом:
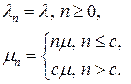 . .
| (7.37) |
Следовательно
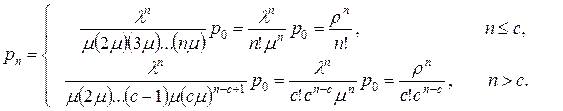 . .
| (7.38) |
Значение вероятности 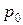 определяется из уравнения
определяется из уравнения 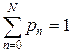 . Если
. Если 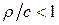 , то мы приходим к следующей формуле для
, то мы приходим к следующей формуле для 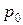 :
:
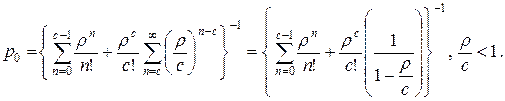
| (7.39) |
Выражение для 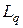 можно найти следующим образом:
можно найти следующим образом:
 . .
| (7.40) |
Поскольку 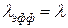 , то
, то  ; значения для
; значения для 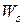 и
и 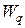 можно найти, разделив на
можно найти, разделив на 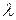 значения
значения 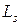 и
и 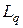 .
.
Пример. В небольшом городке функционируют две службы такси. Каждая из них располагает двумя автомобилями, и по имеющейся информации заказы на обслуживание делятся службами практически поровну. Это подтверждается тем фактом, что заказы в диспетчерские отделения об
Дата добавления: 2016-03-05; просмотров: 2229;
