Теория игр и принятие решений.
В этой главе показаны возможности использования одного из классов игровых моделей – так называемых стратегических игр – для решения задач принятия решений в условиях неопределенности. Дается общее описание стратегической игры. Подробно рассматриваются классы стратегических игр двух лиц с нулевой суммой, а также с постоянной ненулевой суммой. Определяется понятие равновесия в чистых и смешанных стратегиях. Представлен общий подход к решению игры указанного выше типа – сведение ее к задаче линейного программирования. Приведены примеры принятия решений для различных областей.
3.1. Критерии принятия решения.
Человеку постоянно приходится принимать решения. Так, прежде чем выйти из дому, вы задумываетесь над тем, взять ли зонт. Конечно, не хотелось бы носить его с собой в хорошую погоду. Но в дождливый день зонт будет весьма кстати. Так брать или не брать зонт?
Ответить на этот вопрос несложно, если точно знать, какая будет погода. Если с утра идет дождь, большинство людей возьмет зонты. Хотя, возможно, не все. Некоторые закаленные люди скорее предпочтут промокнуть, лишь бы не носить весь день с собой зонт. Последствия отсутствия зонта в плохую погоду оцениваются каждым человеком по-разному. Эти оценки влияют на решение.
Сложнее принять решение, если отсутствует достоверная информация о том, какая ожидается погода. Нельзя полностью доверять прогнозу. Он никогда не бывает абсолютно точным. Еще сложнее принять решение, если вы прогноза не знаете.
Теория принятия решений — это аналитический подход к выбору наилучшей альтернативы или последовательности действий. В теории принятия решений используются "разумные" процедуры выбора наилучшей из нескольких возможных альтернатив. Насколько правильным будет выбор, зависит от качества данных, используемых при описании ситуации, в которой принимается решение. Соответственно существуют три типа моделей, которые зависят от степени определенности возможных исходов или последствий, с которыми сталкивается лицо, принимающее решения (ЛПР).
1. Принятие решений в условиях определенности, когда данные известны точно иЛПР точно знает последствия и исходы любой альтернативы или выбора решения. Например, ЛПР с полной определенностью знает, что вклад 100 тыс. руб. на текущий счет приведет к увеличению баланса этого счета на 100 тыс. руб.
2. Методы принятия решений в условиях отсутствия достоверной информации о возможных последствиях, когда данные можно описать с помощью вероятностных распределений иЛПР знает вероятности наступления исходов или последствий для каждого решения, изучаются теорией риска. Мы можем не знать того, что завтра будет дождь, но мы можем знать, что вероятность дождя 0,3.
Эта теория имеет широкую сферу приложений в экономике. Одно из наиболее важных – выбор инвестиционных проектов.
3. Принятие решений в условиях неопределенности, когда данным нельзя приписать относительные веса (весовые коэффициенты), которые представляли бы степень их значимости в процессе принятия решений.
По существу, в условиях определенности, данные надежно определены, в условиях неопределенности они не определены. Принятие решений в условиях риска, следовательно, представляет "промежуточный" случай.
3.1.1. Принятие решений в условиях определенности – метод
анализа иерархий.
Модели динамического программирования, рассматриваемые в предыдущих разделах, являются примером принятия решений в условиях определенности. Эти модели применимы лишь в тех случаях, когда альтернативные решения можно связать между собой функциональными связями. В этом разделе рассматривается иной подход к принятию решений в ситуациях, когда, например, для идей, чувств, эмоций определяются некоторые количественные
показатели, обеспечивающие числовую шкалу предпочтений для возможных альтернативных решений. Этот подход известен как метод анализа иерархий.
Перед тем как изложить детали данного метода, рассмотрим пример, основной способ, с помощью которого оцениваются различные альтернативные решения. Заметим, что общая структура метода анализа иерархий может включать несколько иерархических уровней со своими критериями.
Пример. Сергей – выпускник - отличник средней школы, который получил полную стипендию от трех университетов: А, В и С. Сестра Сергея - Катя также получила полную стипендию от трех тех же университетов. Однако их родители ставят условие, что дети должны учиться в одном университете, тогда они смогут пользоваться одним автомобилем.
Для того чтобы выбрать университет, Сергей и Катя сформулировали два основных критерия: местонахождение университета и его академическая репутация. Будучи отличным учеником, Сергей оценивает академическую репутацию университета в относительных единицах как 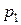 , а его местонахождение как
, а его местонахождение как 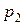 . Катя имеет свою индивидуальную точку зрения относительно критериев местонахождения и академической репутации каждого университета. А именно, местонахождение -
. Катя имеет свою индивидуальную точку зрения относительно критериев местонахождения и академической репутации каждого университета. А именно, местонахождение - 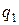 и репутация -
и репутация - 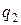 . Какой университет выбрали дети?
. Какой университет выбрали дети?
Решение.Заметим, что 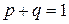 ,
, 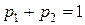 ,
, 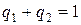 ,
, 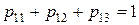 ,
, 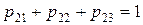 ,
, 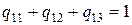 ,
, 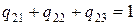 .
.
Сергей и Катя используют метод анализа иерархий (сущность его излагается ниже) для оценки трех университетов с точки зрения их местонахождения, репутации и пожеланий родителей. Определение комбинированного веса для университета А, представленное на рис.3, демонстрирует, каким образом вычисляются эти показатели.

Рис. 3 Расширенная иерархия принятия решения
3.1.2. Методы принятия решений в условиях риска.
Если решение принимается в условиях риска, то стоимости альтернативных решений обычно описываются вероятностными распределениями. По этой причине принимаемое решение основывается на использовании критерия ожидаемого значения, в соответствии с которым альтернативные решения сравниваются с точки зрения максимизации ожидаемой прибыли или минимизации ожидаемых затрат.
Критерий ожидаемого значения сводится либо к максимизации ожидаемой (средней) прибыли, либо к минимизации ожидаемых затрат. В данном случае предполагается, что прибыль (затраты), связанная с каждым альтернативным решением, является случайной величиной.
Постановка таких задач обычно заключается в следующем. Человек выбирает какие-то действия в ситуации, где на получаемый результат (исход) действия влияют случайные события, неподвластные человеку. Но, имея некоторые знания о вероятностях этих событий, человек может рассчитать наиболее выгодную совокупность и очередность своих действий.
Отметим, что в данной постановке задачи варианты действий обычно не оцениваются по многим критериям. Таким образом, используется более простое их описание. Рассматривается не одно, а несколько последовательных действий, что позволяет построить так называемые «деревья решений».
Дерево решений — это графическое изображение процесса решений, в котором отражены альтернативные решения, состояния среды, а также соответствующие вероятности и выигрыши для любых комбинаций альтернатив и состояний среды.
В приведенном ниже примере рассматривается простая ситуация, связанная с принятием решения при наличии конечного числа альтернатив и точных значений матрицы доходов.
Пример.Предположим, что вы хотите вложить на фондовой бирже
100 000 рублей в акции одной из двух компаний: А или В. Акции компании А являются рискованными, но могут принести 50 % прибыли от суммы инвестиции на протяжении следующего года. Если условия фондовой биржи будут неблагоприятны, сумма инвестиции может обесцениться на 20 %. Компания В обеспечивает безопасность инвестиций с 15 % прибыли в условиях повышения котировок на бирже и только 5 % – в условиях понижения котировок. Все аналитические публикации, с которыми можно познакомиться (а они всегда есть в изобилии в конце года), с вероятностью 60 % прогнозируют повышение котировок и с вероятностью 40 % — понижение котировок. В какую компанию следует вложить деньги?
Решение.Эта задача может быть также представлена в виде дерева решений, показанного на рис. 4. На этом рисунке используется два типа вершин: квадратик представляет "решающую" вершину, а кружок— "случайную". Таким образом, из вершины 1 ("решающая") выходят две ветви, представляющие альтернативы, связанные с покупкой акций компании А или В. Далее две ветви, выходящие из "случайных" вершин 2 и 3, соответствуют случаям повышения и понижения котировок на бирже с вероятностями их появления и соответствующими платежами.
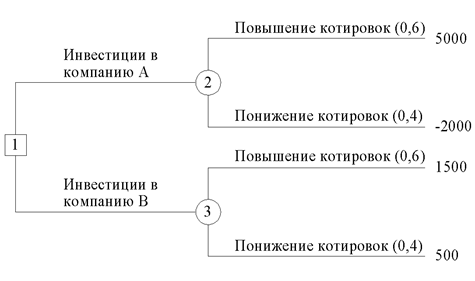
Рис. 4 Дерево решений для задачи инвестирования.
Исходя из этого найдем среднюю ожидаемую прибыль за год для каждой из двух альтернатив.
Для акций компании А: 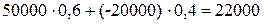 (руб.).
(руб.).
Для акций компании В: 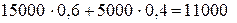 (руб.).
(руб.).
Таким образом, вашим решением, основанным на этих вычислениях, является покупка акций компании А.
В теории принятия решений повышение и понижение котировок на бирже именуются состояниями природы, возможные реализации которых являются случайными событиями (в данном случае с вероятностями 0,6 и 0,4).
В общем случае задача принятия решений может включать 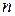 состояний природы и
состояний природы и 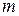 альтернатив. Если
альтернатив. Если 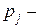 вероятность
вероятность 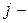 го состояния природы, а
го состояния природы, а 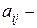 платеж, связанный с принятием решения
платеж, связанный с принятием решения 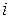 при состоянии природы
при состоянии природы 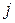 (
( 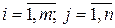 ), тогда ожидаемый платеж для стратегии
), тогда ожидаемый платеж для стратегии 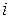 вычисляется в виде
вычисляется в виде
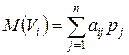 , ,
| (3.1) |
где по определению 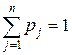 .
.
Наилучшим решением будет то, которое соответствует
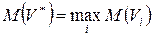 или или 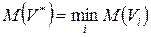 , ,
| (3.2) |
в зависимости от того, является ли платеж в задаче доходом (прибылью) или убытком (затратами).
Предложенный критерий ожидаемого значения, другими словами - математическое ожидание, иногда применяется в других модифицированных вариантах.
Рассмотрим две модификации критерия ожидаемого значения. Первая состоит в определении апостериорных вероятностей на основе эксперимента над исследуемой системой, вторая – в определении полезности реальной стоимости денег.
Апостериорные вероятности Байеса. Распределения вероятностей, которые используются при формулировке критерия ожидаемого значения, получаются, как правило, из накопленной ранее информации . В некоторых случаях
оказывается возможным пересчитать эти вероятности с помощью текущей и/или полученной ранее информации, которая обычно основывается на исследовании выборочных (или экспериментальных) данных. Получаемые при этом вероятности называют апостериорными (или байесовскими), в отличие от априорных вероятностей, полученных из исходной информации. Следующий пример показывает, как рассмотренный выше критерий ожидаемого значения можно модифицировать так, чтобы воспользоваться новой информацией, содержащейся в апостериорных вероятностях.
Пример. В предыдущем примере априорные вероятности 0,6 и 0,4 повышения и понижения котировок акций на бирже были определены из наличных публикаций финансового характера. Предположим, вместо того, чтобы полностью полагаться на эти публикации, вы решили провести личное исследование путем консультаций с другом, который хорошо разбирается в вопросах, касающихся фондовой биржи. Друг высказывает общее мнение "за" или "против" инвестиций. Это мнение в дальнейшем определяется количественно
следующим образом. При повышении котировок его мнение с 90% -ной вероятностью будет "за", при снижении котировок вероятность его мнения "за" уменьшится до 50 %. Каким образом можно извлечь пользу из этой дополнительной информации?
Решение.Мнение друга фактически представляет условные вероятности "за - против" при заданных состояниях природы в виде повышения и понижения котировок. Введем следующие обозначения для данных событий:
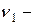 мнение "за",
мнение "за", 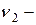 мнение "против",
мнение "против", 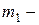 повышение котировок,
повышение котировок, 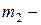 понижение котировок. Мнение друга можно записать в виде вероятностных соотношений следующим образом:
понижение котировок. Мнение друга можно записать в виде вероятностных соотношений следующим образом:
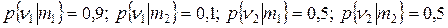
| (3.3) |
С помощью этой дополнительной информации задачу выбора решения можно сформулировать следующим образом.
1. Если мнение друга "за", акции какой компании следует покупать – А или В?
2. Если мнение друга "против", то, опять-таки, акции какой компании следует покупать – А или В?
Рассматриваемую задачу можно представить в виде дерева решений, показанного на рис. 5. Узлу 1 здесь соответствует случайное событие (мнение друга) с соответствующими вероятностями "за" и "против". Узлы 2 и 3 представляют выбор между компаниями А и В при известном мнении друга "за" или "против" соответственно. Узлы 4-7 соответствуют случайным событиям, связанным с повышением и понижением котировок.
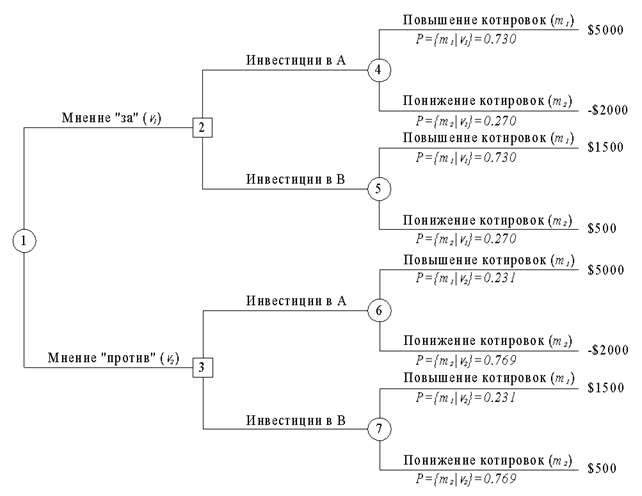
Рис. 5 Дерево решений с апостериорными вероятностями.
Для оценки различных альтернатив, показанных на рис. 5, необходимо вычислить апостериорные вероятности 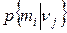 , указанные на соответствующих ветвях, выходящих из узлов 4-7. Эти апостериорные вероятности вычисляются с учетом дополнительной информации, содержащейся в рекомендациях друга, с помощью следующих действий.
, указанные на соответствующих ветвях, выходящих из узлов 4-7. Эти апостериорные вероятности вычисляются с учетом дополнительной информации, содержащейся в рекомендациях друга, с помощью следующих действий.
Шаг 1.
Условные вероятности 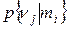 для данной задачи запишем следующим образом
для данной задачи запишем следующим образом
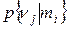
| 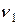
| 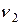
| |
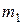
| 0,9 | 0,1 | |
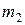
| 0,5 | 0,5 |
Шаг 2. Вычисляем вероятности совместного появления событий.
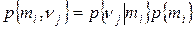 . .
| (3.4) |
При заданных априорных вероятностях 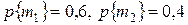 вероятности совместного появления событий определяются умножением первой и второй строк таблицы, полученной на шаге 1, на 0,6 и 0,4 соответственно. В результате имеем следующее
вероятности совместного появления событий определяются умножением первой и второй строк таблицы, полученной на шаге 1, на 0,6 и 0,4 соответственно. В результате имеем следующее
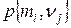
| 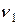
| 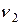
| |
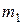
| 0,54 | 0,06 | |
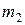
| 0,2 | 0,2 |
Сумма всех элементов этой таблицы равна 1.
Шаг З. Вычисляем абсолютные вероятности.
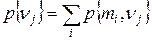 . .
| (3.5) |
Эти вероятности получаются путем суммирования элементов соответствующих столбцов таблицы, полученной на шаге 2. В итоге имеем следующее.
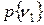
| 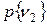
|
| 0,74 | 0,26 |
Шаг 4. Определяем искомые апостериорные вероятности по формуле
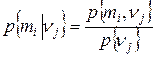 . .
| (3.6) |
Эти вероятности вычисляются в результате деления каждого столбца таблицы, полученной на шаге 2, на элемент соответствующего столбца таблицы, вычисленной на шаге 3, что приводит к следующим результатам (округленным до трех десятичных знаков).
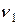
| 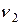
| |
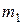
| 0,730 | 0,231 |
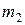
| 0,270 | 0,769 |
Это те вероятности, которые показаны на рис. 5. Они отличаются от исходных априорных вероятностей 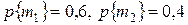 .
.
Теперь можно оценить альтернативные решения, основанные на ожидаемых платежах для узлов 4-7.
Мнение «за».Доход от акций компании А в узле 4 равен
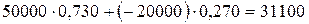 руб.
руб.
Доход от акций компании В в узле 5 равен
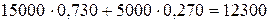 руб.
руб.
Ответ. Инвестировать в акции компании А.
Мнение «против» .Доход от акций компании А в узле 6 равен
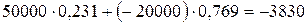 руб.
руб.
Доход от акций компании В в узле 7 равен
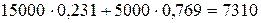 руб.
руб.
Ответ. Инвестировать в акции компании В.
3.1.3. Принятие решений в условиях неопределенности
В условиях неопределенностиЛПР не знает вероятностей наступления исходов для каждого решения. Например, вероятность того, что весь тираж этой книги будет реализован за год, авторам неизвестна.
Если имеет место полная неопределенность в отношении возможности реализации состояний среды (т.е. мы не можем даже приблизительно указать вероятности наступления каждого возможного исхода), то обстоятельства, с которыми мы имеем дело при выборе решения, можно представить как вид стратегической игры, в которой один игрок – ЛПР, а другой – некая объективная действительность, называемая природой. Условия такой игры обычно представляются следующей таблицей решений, в которой строки 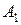 ,
, 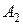 , ...,
, ..., 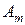 , соответствуют стратегиям ЛПР, а столбцы
, соответствуют стратегиям ЛПР, а столбцы 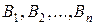 — стратегиям природы (
— стратегиям природы ( 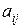 — выигрыш ЛПР, соответствующий каждой паре
— выигрыш ЛПР, соответствующий каждой паре 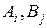 ):
):
Таблица 16.
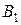
| 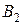
| 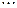
| 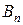
| |
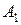
| 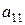
| 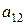
| 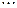
| 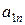
|
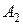
| 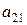
| 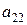
| 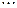
| 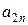
|
| 
| 
| 
| 
|
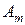
| 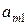
| 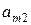
| 
| 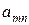
|
В рассматриваемой ситуации при выборе из множества { 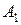 ,
, 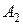 ,...,
,..., 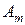 } наилучшего решения обычно используют следующие критерии:
} наилучшего решения обычно используют следующие критерии:
1. Максимаксный критерий, или критерий крайнего оптимизма –определяет альтернативу, которая максимизирует максимальный результат для каждой альтернативы, т.е. ЛПР выбирает стратегию, которой соответствует
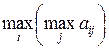 . .
| (3.7) |
2. Максиминный критерий Вальда, или критерий крайнего пессимизма –определяет альтернативу, которая максимизирует минимальный результат для каждой альтернативы, т.е. ЛПР выбирает стратегию 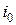 , которой соответствует
, которой соответствует
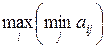 . .
| (3.8) |
3. Критерий минимаксного риска Сэвиджа. Согласно этому критерию выбирается стратегия, при которой величина риска 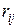 в наихудших условиях минимальна, т.е. равна
в наихудших условиях минимальна, т.е. равна
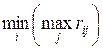 . .
| (3.9) |
Здесь риск 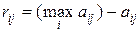 .
.
4. Критерий оптимизма-пессимизма Гурвица –рекомендует при выборе решения не руководствоваться ни крайним пессимизмом, ни крайним оптимизмом. Согласно этому критерию стратегия выбирается из условия
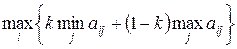 . .
| (3.10) |
Значение коэффициента пессимизма k выбирается между нулем и единицей. При k = 1 критерий Гурвица превращается в критерий Вальда, при k = 0 –в критерий крайнего оптимизма.
5. Критерий безразличия. В условиях полной неопределенности предполагается, что все возможные состояния среды (природы) равновероятны. Этот критерий выявляет альтернативу с максимальным средним результатом, т.е.
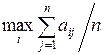 . .
| (3.11) |
Если известна таблица решений с оценками условий и вероятностями реализации для всех состояний среды, можно определить ожидаемую стоимостную оценку 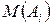 для каждой альтернативы. Один из наиболее распространенных критериев выбора альтернативы – выбор альтернативы с максимальным значением
для каждой альтернативы. Один из наиболее распространенных критериев выбора альтернативы – выбор альтернативы с максимальным значением 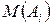 .
.
Для каждой альтернативы ожидаемая стоимостная оценка 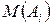 есть сумма всевозможных оценок условий (выигрышей) для этой альтернативы, умноженных на вероятности реализации этих выигрышей:
есть сумма всевозможных оценок условий (выигрышей) для этой альтернативы, умноженных на вероятности реализации этих выигрышей:
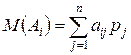 . .
| (3.12) |
где 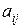 – выигрыш ЛПР при выборе альтернативы i и реализации состояния среды j, j =1,..., n;
– выигрыш ЛПР при выборе альтернативы i и реализации состояния среды j, j =1,..., n; 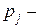 вероятность наступления состояния среды j.
вероятность наступления состояния среды j.
Ожидаемой ценностью достоверной информации 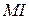 назовем разность между выигрышем в условиях определенности и выигрышем в условиях риска.
назовем разность между выигрышем в условиях определенности и выигрышем в условиях риска.
Для того чтобы определить 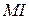 , вначале необходимо рассчитать математическое ожидание в условиях определенности, которое равно ожидаемому (или среднему) доходу в случае, когда мы имеем достоверную информацию перед тем, как принять решение. Ожидаемый выигрыш в условиях достоверной информации определяется как
, вначале необходимо рассчитать математическое ожидание в условиях определенности, которое равно ожидаемому (или среднему) доходу в случае, когда мы имеем достоверную информацию перед тем, как принять решение. Ожидаемый выигрыш в условиях достоверной информации определяется как
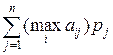 . .
| (3.13) |
Тогда
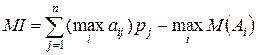 . .
| (3.14) |
Таблицу решений удобно использовать при анализе задач, имеющих одно множество альтернативных решений и одно множество состояний среды. Многие задачи, однако, содержат последовательности решений и состояний среды. Если имеют место два (или более) последовательных решения и последующее решение основывается на исходе предыдущего, более предпочтителен подход, основанный на построении дерева решений, как это сделано в п. 3.2.
Анализ задач с помощью дерева решений включает пять этапов:
1) формулировка задачи;
2) построение дерева решений;
3) оценка вероятностей состояний среды;
4) установление выигрышей для каждой возможной комбинации альтернатив и состояний среды;
5) решение задачи путем расчета ожидаемой стоимостной оценки 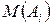 для каждой вершины состояния среды.
для каждой вершины состояния среды.
Пример.Компания «Буренка» изучает возможность производства и сбыта навесов для хранения кормов. Проект может основываться на большой или малой производственной базе. Рынок для реализации навесов может быть благоприятным или неблагоприятным. Василий Бычков – менеджер компании – учитывает возможность вообще не производить эти навесы.
При благоприятной рыночной ситуации большое производство позволило бы Бычкову получить чистую прибыль 200 тыс. руб. Если рынок окажется неблагоприятным, то при большом производстве компания понесет убытки в размере 180 тыс. руб. Малое производство дает 100 тыс. руб. прибыли при благоприятной рыночной ситуации и 20 тыс. руб. убытков при неблагоприятной.
Вопрос: Какую альтернативу следует выбрать?
Решение. Для анализа ситуации применим перечисленные выше критерии. Составим таблицу решений (k = 0,75):
Таблица 17.
| Альтернатива | Состояние среды Критерии | |||||||
| Благо- прият-ный рынок | Неблаго- прият-ный рынок | Maximax | Maximin | Критерий Сэвиджа | Критерий Гурвица | Критерий безразли- чия | ||
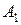
| Создать большое производство | -180 | -180 | -85 | ||||
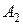
| Создать малое производство | -20 | -20 | |||||
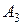
| Ничего не делать |
Ответ: По критерию maximax следует выбрать альтернативу 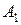 ; по критерию maximin и критерию Гурвица (при k=0,75) –
; по критерию maximin и критерию Гурвица (при k=0,75) – 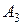 ; по критерию минимума максимального риска (критерию Сэвиджа) и критерию безразличия –
; по критерию минимума максимального риска (критерию Сэвиджа) и критерию безразличия – 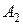 .
.
3.2. Игровые методы обоснования решений.
3.2.1. Основные определения.
Впредыдущих разделах мы рассматривали вопросы, связанные с математическим моделированием (а иногда и оптимизацией решений), в случаях, когда условия операции содержат стохастическую неопределенность, которая в принципе может быть учтена, если знать законы распределения.
Такая неопределенность – еще «полбеды». Теперь рассмотрим гораздо худший вид неопределенности, когда некоторые параметры, от которых зависит успех операции, неизвестны. Такого рода задачами занимается специальный раздел математики, носящий название «теория игр и статистических решений». В некоторых (редких) случаях разработанные в нем методы дают возможность фактически найти оптимальное решение. Гораздо чаще эти методы позволяют попросту глубже разобраться в ситуации, оценить каждое решение с различных (иногда противоречивых) точек зрения, взвесить его преимущества и недостатки и, в конце концов, принять решение, если не единственно правильное, то, по крайней мере, до конца продуманное.
Наиболее простыми из таких ситуаций являются так называемые конфликтные ситуации. Так называются ситуации, в которых сталкиваются интересы двух (или более) сторон, преследующих разные (иногда противоположные) цели, причем выигрыш каждой стороны зависит от того, как себя поведут другие.
Теория игр представляет собой математическую теорию конфликтных ситуаций. Ее цель – выработка рекомендаций по разумному поведению участников конфликта. Каждая непосредственно взятая из практики конфликтная ситуация очень сложна, и ее анализ затруднен наличием привходящих, несущественных факторов. Чтобы сделать возможным математический анализ конфликта, строится его математическая модель, Такую модель называют игрой.
От реального конфликта игра отличается тем, что ведется по определенным правилам. Эти правила указывают «права и обязанности» участников, а также исход игры – выигрыш или проигрыш каждого участника в зависимости от сложившейся обстановки.
В игре могут сталкиваться интересы двух или более участников; в первом случае игра называется «парной», во втором – «множественной». Развитие игры во времени можно представлять как ряд последовательных «ходов» участников. Ходом называется выбор игроком одного из предусмотренных правилами игры действий и его осуществление. Ходы бывают личные и случайные. При личном ходе игрок сознательно выбирает и осуществляет тот или другой вариант действий (пример – любой ход в шахматах). При случайном ходе выбор осуществляется не волей игрока, а каким-то механизмом случайного выбора (бросание монеты, игральной кости, вынимание карты из колоды и т. п.). Некоторые игры (так называемые «чисто азартные») состоят только из случайных ходов – ими теория игр не занимается. Ее цель – оптимизация поведения игрока в игре, где (может быть, наряду со случайными) есть личные ходы. Такие игры называются стратегическими.
Стратегией игрока называется совокупность правил, определяющих выбор варианта действий при каждом личном ходе в зависимости от сложившейся ситуации. В зависимости от числа стратегий игры делятся на «конечные» и «бесконечные». Игра называется конечной, если у каждого игрока имеется в распоряжении только конечное число стратегий (в противном случае игра называется бесконечной). Бывают игры (например, шахматы), где в принципе число стратегий конечно, но так велико, что полный их перебор практически невозможен.
Оптимальной стратегией игрока называется такая, которая обеспечивает ему наилучшее положение в данной игре, т. е. максимальный выигрыш. Если игра повторяется неоднократно и содержит, кроме личных, еще и случайные ходы, оптимальная стратегия обеспечивает максимальный средний выигрыш.
Задача теории игр – выявление оптимальных стратегий игроков. Основное предположение, исходя из которого находятся оптимальные стратегии, состоит в том, что противник (в общем случае – противники) по меньшей мере, так же разумен, как и сам игрок, и делает все для того, чтобы добиться своей цели. Расчет на разумного противника – лишь одна из возможных позиций в конфликте, но в теории игр именно она кладется в основу.
Игра называется игрой с нулевой суммой, если сумма выигрышей всех игроков равна нулю (т. е. каждый игрок выигрывает только за счет других). Самый простой случай — парная игра с нулевой суммой — называется антагонистической (или игрой со строгим соперничеством). Теория антагонистических игр – наиболее развитый раздел теории игр, с четкими рекомендациями.
Теория игр, как и всякая математическая модель, имеет свои ограничения. Одним из них является предположение о полной («идеальной») разумности противника (противников). В реальном конфликте зачастую оптимальная стратегия состоит в том, чтобы угадать, в чем противник «глуп», и воспользоваться этой глупостью в свою пользу. В теории игр выявляется наиболее осторожное, «перестраховочное» поведение участников конфликта.
3.2.2. Игры двух лиц с нулевой суммой.
В теории игр рассматриваются ситуации, связанные с принятием решений, в которых два разумных противника имеют конфликтующие цели. К числу типичных примеров относится рекламирование конкурирующих товаров и планирование военных стратегий противоборствующих армий. Эти ситуации принятия решений отличаются от рассмотренных ранее, где природа не рассматривается в роли недоброжелателя. В игровом конфликте участвуют два противника, именуемые игроками, каждый из которых имеет некоторое множество (конечное или бесконечное) возможных выборов, которые называются стратегиями. С каждой парой стратегий связан платеж, который один из игроков выплачивает другому. Такие игры известны как игры двух
лиц с нулевой суммой, так как выигрыш одного игрока равен проигрышу другого. В такой игре достаточно задать результаты в виде платежей для одного из игроков. При обозначении игроков через  и
и  с числом стратегий
с числом стратегий 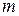 и
и 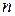 соответственно игру обычно представляют в виде матрицы платежей игроку
соответственно игру обычно представляют в виде матрицы платежей игроку  :
:
Таблица 18.
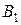
| 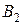
| 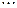
| 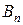
| |
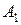
| 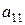
| 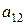
| 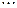
| 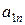
|
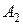
| 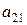
| 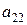
| 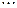
| 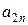
|
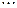
| 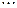
| 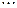
| 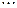
| 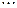
|
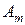
| 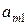
| 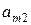
| 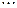
| 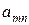
|
Такое представление матричной игры означает, что если игрок  использует стратегию
использует стратегию 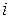 , а игрок
, а игрок  – стратегию
– стратегию 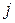 , то платеж игроку
, то платеж игроку  составляет
составляет 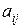 и, следовательно, игроку
и, следовательно, игроку  платеж составит
платеж составит 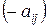 . Очевидно, исходя из принципа осторожности (а он – основной принцип теории игр), надо выбрать ту стратегию, при которой наш минимальный выигрыш максимален. Это – так называемый «принцип минимакса»: поступай так, чтобы при наихудшем для тебя поведении противника получить максимальный выигрыш.
. Очевидно, исходя из принципа осторожности (а он – основной принцип теории игр), надо выбрать ту стратегию, при которой наш минимальный выигрыш максимален. Это – так называемый «принцип минимакса»: поступай так, чтобы при наихудшем для тебя поведении противника получить максимальный выигрыш.
Поскольку игры берут свое начало в конфликте интересов, оптимальным решением игры является одна или несколько таких стратегий для каждого из игроков, при этом любое отклонение от данных стратегий не улучшает плату тому или другому игроку. Эти решения могут быть в виде единственной чистой стратегии или нескольких стратегий, которые являются смешанными в соответствии с заданными вероятностями. Рассматриваемые ниже примеры демонстрируют перечисленные ситуации.
Пример. Две компании А и В продают два вида лекарств против гриппа. Компания А рекламирует продукцию на радио (А1), телевидении (А2) и в газетах (А3). Компания В, в дополнение к использованию радио (B1), телевидения (В2) и газет (В3), рассылает также по почте брошюры (В4). В зависимости от умения и интенсивности проведения рекламной кампании, каждая из компаний может привлечь на свою сторону часть клиентов конкурирующей компании. Приведенная ниже матрица характеризует процент клиентов, привлеченных или потерянных компанией А.
Таблица 19.
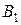
| 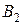
| 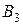
| 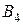
| Минимумы
cтрок 
| |
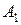
| -2 | -3 | -3 | ||
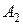
| 5 (максимин) | ||||
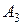
| -2 | -9 | -9 | ||
Максимумы
столбцов 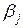
| 5 (минимакс) |
Решение игры основано на обеспечении наилучшего результата из наихудших для каждого игрока. Если компания  выбирает стратегию
выбирает стратегию 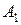 , то, независимо от того, что предпринимает компания
, то, независимо от того, что предпринимает компания  , наихудшим результатом является потеря компанией
, наихудшим результатом является потеря компанией  3 % рынка в пользу компании
3 % рынка в пользу компании  . Это определяется минимумом элементов первой строки матрицы платежей. Аналогично при выборе стратегии
. Это определяется минимумом элементов первой строки матрицы платежей. Аналогично при выборе стратегии 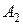 наихудшим исходом для компании
наихудшим исходом для компании  является увеличение рынка на 5 % за счет компании
является увеличение рынка на 5 % за счет компании  . Наконец, наихудшим исходом при выборе стратегии
. Наконец, наихудшим исходом при выборе стратегии 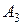 является потеря компанией
является потеря компанией  9 % рынка в пользу компании
9 % рынка в пользу компании  . Эти результаты содержатся в столбце "Минимумы строк". Чтобы достичь наилучшего результата из наихудших, компания
. Эти результаты содержатся в столбце "Минимумы строк". Чтобы достичь наилучшего результата из наихудших, компания  выбирает стратегию
выбирает стратегию 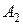 , так как она соответствует наибольшему элементу столбца "Минимумы строк".
, так как она соответствует наибольшему элементу столбца "Минимумы строк".
Рассмотрим теперь стратегии компании  . Так как элементы матрицы являются
. Так как элементы матрицы являются
платежами компании  , критерий наилучшего результата из наихудших для компании
, критерий наилучшего результата из наихудших для компании  соответствует выбору минимаксного значения. В результате приходим к выводу, что выбором компании
соответствует выбору минимаксного значения. В результате приходим к выводу, что выбором компании  является стратегия
является стратегия 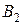 . Оптимальным решением в игре является выбор стратегий
. Оптимальным решением в игре является выбор стратегий 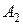 и
и 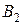 , т.е. обеим компаниям следует проводить рекламу на телевидении. При этом выигрыш будет в пользу компании
, т.е. обеим компаниям следует проводить рекламу на телевидении. При этом выигрыш будет в пользу компании  , так как ее рынок увеличится на 5 %. В этом случае говорят, что цена игры равна 5 % и что компании
, так как ее рынок увеличится на 5 %. В этом случае говорят, что цена игры равна 5 % и что компании  и
и  используют стратегии, соответствующие седловой точке.
используют стратегии, соответствующие седловой точке.
Итак, исходя из принципа осторожности (перестраховочного правила «всегда рассчитывай на худшее!»), компания  должна выбрать стратегию А2, а противник — стратегию В2. Такие стратегии называются «минимаксными» (вытекающими из принципа минимакса). До тех пор, пока обе стороны в нашем примере будут придерживаться своих минимаксных стратегий, выигрыш будет равен
должна выбрать стратегию А2, а противник — стратегию В2. Такие стратегии называются «минимаксными» (вытекающими из принципа минимакса). До тех пор, пока обе стороны в нашем примере будут придерживаться своих минимаксных стратегий, выигрыш будет равен 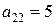 .
.
Решение, соответствующее седловой точке, гарантирует, что ни одной компании нет смысла пытаться выбрать другую стратегию. Действительно, если компания  переходит к другой стратегии (
переходит к другой стратегии ( 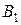 ,
, 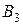 или
или 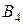 ), то компания
), то компания  может сохранить свой выбор стратегии
может сохранить свой выбор стратегии 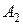 , что приведет к большей потере рынка компанией
, что приведет к большей потере рынка компанией  (6 или 8 %). По тем же причинам компании
(6 или 8 %). По тем же причинам компании  нет резона использовать другую стратегию, ибо если она применит, например, стратегию
нет резона использовать другую стратегию, ибо если она применит, например, стратегию 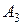 , то компания
, то компания  может использовать свою стратегию
может использовать свою стратегию 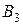 и увеличить свой рынок на 9 %. Аналогичные выводы имеют место, если компания
и увеличить свой рынок на 9 %. Аналогичные выводы имеют место, если компания  будет использовать стратегию
будет использовать стратегию 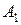 .
.
Обозначим 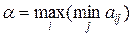 и назовем её нижней ценой игры. Величину
и назовем её нижней ценой игры. Величину 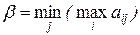 назовем верхней ценой игры. Признак наличия седловой точки и уравновешенной пары стратегий – это равенство нижней и верхней цены игры; общее значение α и β называется ценой игры. Мы будем обозначать его
назовем верхней ценой игры. Признак наличия седловой точки и уравновешенной пары стратегий – это равенство нижней и верхней цены игры; общее значение α и β называется ценой игры. Мы будем обозначать его 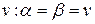 .
.
Стратегии 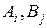 (в данном случае
(в данном случае 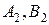 ), при которых этот выигрыш достигается, называются оптимальными чистыми стратегиями, а их совокупность – решением игры. Про саму игру в этом случае говорят, что она решается в чистых стратегиях. Обеим сторонам А и В можно указать их оптимальные стратегии, при которых их положение – наилучшее из возможных. А что игрок А при этом выигрывает 5, а игрок В –проигрывает 5, – что же, таковы условия игры: они выгодны для А и невыгодны для В.
), при которых этот выигрыш достигается, называются оптимальными чистыми стратегиями, а их совокупность – решением игры. Про саму игру в этом случае говорят, что она решается в чистых стратегиях. Обеим сторонам А и В можно указать их оптимальные стратегии, при которых их положение – наилучшее из возможных. А что игрок А при этом выигрывает 5, а игрок В –проигрывает 5, – что же, таковы условия игры: они выгодны для А и невыгодны для В.
Почему оптимальные стратегии называются «чистыми»? Бывают стратегии «смешанные», состоящие в том, что игрок применяет не одну какую-то стратегию, а несколько, перемежая их случайным образом. Наличие седловой точки в игре – это далеко не правило, скорее – исключение. Большинство игр не имеет седловой точки.
А теперь спросим себя, как быть, если игра не имеет седловой точки: α ≠ β ? Ну что же, если каждый игрок вынужден выбрать одну-единственную чистую стратегию, то делать нечего: надо руководствоваться принципом минимакса. Другое дело, если можно свои стратегии «смешивать», чередовать случайным образом с какими-то вероятностями. Можно показать, что если допустить кроме чистых еще и смешанные стратегии, всякая конечная игра имеет решение – точку равновесия.
Рассмотрим пример игры без седловой точки и приведем (без доказательства) ее решение.
3.2.3. Решение матричных игр в смешанных стратегиях.
Решение матричных игр в смешанных стратегиях может быть найдено либо графически, либо методами линейного программирования. Графический метод применим для решения игр, в которых хоть один игрок имеет две чистые стратегии. Этот метод интересен в том плане, что графически объясняет понятие седловой точки. Методами линейного программирования может быть решена любая игра двух лиц с нулевой суммой.
Пример. Рассмотрим следующую игру 2x4, в которой платежи выплачиваются игроку А.
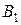
| 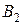
| 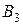
| 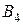
| |
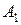
| -1 | |||
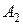
|
Игра не имеет решения в чистых стратегиях, и, следовательно, стратегии должны быть смешанными.
Игра предполагает, что игрок  смешивает стратегии
смешивает стратегии 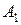 и
и 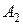 с соответствующими вероятностями
с соответствующими вероятностями 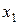 и
и 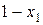 ,
, 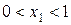 . Игрок
. Игрок  смешивает стратегии
смешивает стратегии 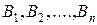 с вероятностями
с вероятностями 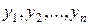 , где
, где 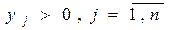 и
и 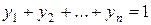 . В этом случае ожидаемый выигрыш игрока
. В этом случае ожидаемый выигрыш игрока  , соответствующий
, соответствующий 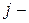 ой чистой стратегии игрока
ой чистой стратегии игрока  , вычисляется в виде
, вычисляется в виде
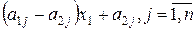 . .
| (3.15) |
Следовательно, игрок  ищет величину
ищет величину 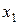 , которая максимизирует минимум ожидаемых выигрышей
, которая максимизирует минимум ожидаемых выигрышей
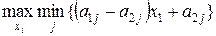 . .
| (3.16) |
Ожидаемые выигрыши игрока  , соответствующие чистым стратегиям игрока
, соответствующие чистым стратегиям игрока  , приведены в следующей таблице.
, приведены в следующей таблице.
Таблица 20.
Чистые стратегии игрока 
| Ожидаемые выигрыши игрока 
|
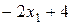
| |
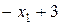
| |
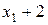
| |
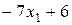
|
На рис. 6 изображены четыре прямые линии, соответствующие чистым стратегиям игрока  . Чтобы определить наилучший результат из наихудших, построена нижняя огибающая четырех указанных прямых (изображенная на рисунке толстыми линейными сегментами), которая представляет минимальный (наихудший) выигрыш для игрока
. Чтобы определить наилучший результат из наихудших, построена нижняя огибающая четырех указанных прямых (изображенная на рисунке толстыми линейными сегментами), которая представляет минимальный (наихудший) выигрыш для игрока  независимо от того, что делает игрок
независимо от того, что делает игрок  . Максимум (наилучшее) нижней огибающей соответствует максиминному решению в точке
. Максимум (наилучшее) нижней огибающей соответствует максиминному решению в точке 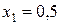 . Эта точка определяется пересеченияем прямых 3 и 4. Следовательно, оптимальным решением для игрока
. Эта точка определяется пересеченияем прямых 3 и 4. Следовательно, оптимальным решением для игрока  является смешивание стратегий
является смешивание стратегий 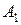 и
и 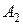 с вероятностями 0,5 и 0,5 соответственно. Соответствующая цена игры
с вероятностями 0,5 и 0,5 соответственно. Соответствующая цена игры 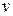 определяется подстановкой
определяется подстановкой 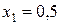 в уравнение либо прямой 3, либо 4, что приводит к следующему
в уравнение либо прямой 3, либо 4, что приводит к следующему
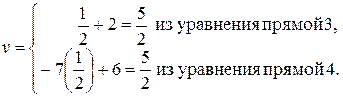 . .
| (3.17) |
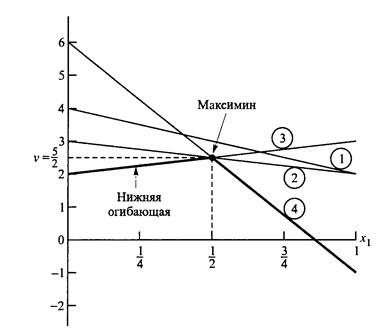
Рис. 6. Графическое решение игры двух лиц с нулевой суммой.
Оптимальная смешанная стратегия игрока  определяется двумя стратегиями, которые формируют нижнюю огибающую графика. Это значит, что игрок
определяется двумя стратегиями, которые формируют нижнюю огибающую графика. Это значит, что игрок  может смешивать стратегии
может смешивать стратегии 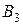 и
и 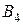 , в этом случае
, в этом случае 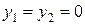 и
и 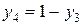 . Следовательно, ожидаемые платежи игрока
. Следовательно, ожидаемые платежи игрока  , соответствующие чистым стратегиям игрока
, соответствующие чистым стратегиям игрока  , имеют такой вид.
, имеют такой вид.
Таблица 21.
Чистые стратегии игрока 
| Ожидаемые выигрыши игрока 
|
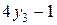
| |
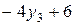
|
Наилучшее решение из наихудших для игрока  представляет собой точку минимума верхней огибающей заданных двух прямых (построение прямых и определение верхней огибающей будет для вас поучительным). Эта процедура эквивалентна решению уравнения
представляет собой точку минимума верхней огибающей заданных двух прямых (построение прямых и определение верхней огибающей будет для вас поучительным). Эта процедура эквивалентна решению уравнения
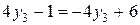 . .
|
Его решением будет 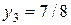 , что определяет цену игры
, что определяет цену игры 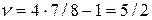 . Таким образом, решением игры для игрока
. Таким образом, решением игры для игрока  является смешивание стратегий
является смешивание стратегий 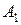 и
и 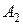 с равными вероятностями 0,5 и 0,5, а для игрока
с равными вероятностями 0,5 и 0,5, а для игрока  – смешивание стратегий
– смешивание стратегий 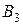 и
и 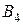 , с вероятностями 7/8 и 1/8.
, с вероятностями 7/8 и 1/8.
Если платежная матрица такова, что каждый элемент некоторой строки 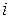 не меньше соответствующего элемента строки к и по меньшей мере один ее элемент строго больше соответствующего элемента строки к, то говорят, что стратегия
не меньше соответствующего элемента строки к и по меньшей мере один ее элемент строго больше соответствующего элемента строки к, то говорят, что стратегия 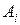 , - игрока 1 доминирует его стратегию
, - игрока 1 доминирует его стратегию 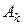 . Доминируемая стратегия
. Доминируемая стратегия 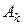 не может быть оптимальной чистой стратегией игрока 1, или войти в его оптимальную смешанную стратегию с ненулевой вероятностью, поэтому ее можно исключить из рассмотрения, вычеркнув из матрицы строку к. Аналогично, если каждый элемент некоторого столбца j не больше соответствующего элемента столбца
не может быть оптимальной чистой стратегией игрока 1, или войти в его оптимальную смешанную стратегию с ненулевой вероятностью, поэтому ее можно исключить из рассмотрения, вычеркнув из матрицы строку к. Аналогично, если каждый элемент некоторого столбца j не больше соответствующего элемента столбца 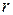 и, по меньшей мере, один его элемент строго меньше соответствующего элемента столбца
и, по меньшей мере, один его элемент строго меньше соответствующего элемента столбца 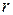 , то говорят, что стратегия
, то говорят, что стратегия 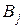 игрока 2 доминирует его стратегию
игрока 2 доминирует его стратегию 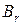 .Поэтому столбец
.Поэтому столбец 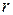 матрицы можно вычеркнуть.
матрицы можно вычеркнуть.
3.2.4. Решение матричных игр методами линейного программирования.
При отсутствии седловой точки общим методом нахождения решения игры любой (конечной) размерности является сведение игры двух лиц с нулевой суммой к задаче линейного программирования. Из основного положения теории стратегических игр следует, что при использовании смешанных стратегий существует, по меньшей мере, одно оптимальное решение с ценой игры 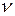 , причем
, причем 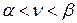 , т.е. цена игры находится между верхним и нижним значениями игры. Величина
, т.е. цена игры находится между верхним и нижним значениями игры. Величина 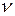 неизвестна, но всегда можно предположить, что
неизвестна, но всегда можно предположить, что 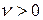 . Это условие выполняется, поскольку всегда можно путем соответствующего преобразования матрицы сделать все ее элементы положительными. Таким образом, е
. Это условие выполняется, поскольку всегда можно путем соответствующего преобразования матрицы сделать все ее элементы положительными. Таким образом, е
Дата добавления: 2016-03-05; просмотров: 2846;
