Измерительные шкалы.
Рациональное использование информации, получаемой от экспертов, возможно при условии преобразования ее в форму, удобную для дальнейшего анализа, направленного на подготовку и принятие решений.
Если эксперт в состоянии сравнить и оценить возможные варианты действий, приписав каждому из них определенное число, будем считать, что он обладает определенной системой предпочтений.
В зависимости от того, по какой шкале могут быть заданы эти предпочтения, экспертные оценки содержат больший или меньший объем информации и обладают различной способностью к математической формализации.
В жизни мы привыкли пользоваться количественными показателями, выраженными в разных измерительных шкалах. Можно записать, что вес тела равен 5 кг, но можно использовать и другую шкалу – 5000 г или 0,005 т, но можно указать интервал: «вес тела больше 3 кг и меньше 10 кг» или «вес тела в пределах первого десятка». Вместо «750 мм ртутного столба» можно записать «1000 гектопаскалей», а можно указать, что «атмосферное давление несколько выше нормы». «451 градус по Фаренгейту» (температура возгорания бумаги) – это «232,78 градусов Цельсия» или «505,93 градусов Кельвина». Понятия «шкала измерения», «тип шкалы», «допустимые преобразования» играют важную роль в теории измерений.
Рассмотрим основные логические аксиомы, используемые в экспертных методах при формализации информации с помощью различных шкал.
5.1. Дихотомическая (номинальная) шкала.
Если различные градации шкалы измерения показателя нельзя упорядочить по условию «больше – меньше» («лучше – хуже») или расположить в порядке появления во времени, то такая совокупность градаций образует шкалу наименований. Шкалу наименований имеют показатели, градации которых могут быть заданы только в виде перечня. В частности, шкала, содержащая всего две градации – «есть» и «нет» (дихотомическая) – является шкалой наименований. Характеристикой центральной тенденции (среднего) на шкале наименований может служить «мода» – значение показателя, которое указано наибольшим числом экспертов, или же наибольшее число раз встретилось в проведённом статистическом исследовании (если речь идёт, например, о видах дефектов продукции). Для небольшого числа оценок эта характеристика также теряет смысл, и тогда центральную тенденцию характеризовать невозможно. Если в распределении двум (или нескольким) каким-либо значениям показателя соответствуют приблизительно одинаковые числа оценок, распределение называют бимодальным (полимодальным).
При использовании номинальных шкал исследуемые объекты можно опознавать на основе трех аксиом идентификации:
1) Х либо есть Y, либо есть не Y;
2) если Х есть Y, то Y есть Х;
3) если Х есть Y, и Y есть Z, то Х есть Z.
Дихотомическая шкала позволяет отметить, относится ли данный объект к интересующей нас группе или нет.
Пример. Две сравниваемые переменные X (семейное положение) и Y (отчисление из института) измеряются в дихотомической шкале (табл.22).
Для вычисления коэффициента корреляции Пирсона составляется таблица сопряжённости (табл.23).
Таблица 22
| № испытуемого | Значение Х | Значение Y |
По этим данным построим корреляционную таблицу
Таблица 23.
| Признак Х Признак Y | Всего | ||
| А=2 | В=3 | А+В=5 | |
| С=4 | D=1 | C+D=5 | |
| Всего | А+С=6 | В+D=4 |
Вычисление коэффициента корреляции Пирсона для дихотомических данных проводится по формуле
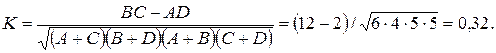
| (5.1) |
Напомним, что при 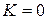 случайные величины
случайные величины 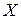 и
и 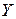 являются независимыми, а при
являются независимыми, а при 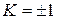 связь между ними линейная. Так как в нашем случае
связь между ними линейная. Так как в нашем случае 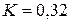 , то корреляция между величинами существует, но непрямая (
, то корреляция между величинами существует, но непрямая ( 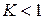 ).
).
5.2. Шкала наименований.
Шкала наименований (номинальная), в которой числа используются исключительно с целью обозначения объектов. Кроме сравнения на совпадение, любые арифметические действия над числами, обозначающими имена объектов, бессмысленны. С помощью шкалы наименований часто отмечают, присутствует или отсутствует какой-то признак в объекте.
Аксиомы тождества:
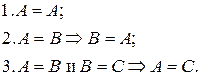
| (5.2) |
Допустимые операции:
– символ Кронекера 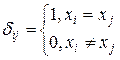 ;
;
– число наблюдений 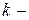 го класса;
го класса; 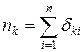 ;
;
– относительная частота класса 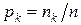 ;
;
– мода 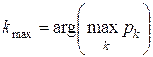 ;
;
– коэффициент согласия (конкордации);
– проверка по тесту 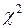 .
.
Примеры номинальных шкал: названия болезней; почтовые, телефонные, автомобильные индексы регионов и стран; пол человека.
5.3. Шкала порядков (ранговые шкалы).
В случаях, когда исследуемые объекты можно в результате сравнения расположить в определенной последовательности с учетом какого-либо существенного фактора (факторов), используются порядковые шкалы, позволяющие устанавливать равноценность или доминирование.
Шкала порядков (ранговая шкала), при измерении в которой мы получаем информацию лишь о том, в каком порядке объекты следуют друг за другом по какому-то свойству. Примером могут служить шкалы, по которым измеряются твёрдость материалов, «похожесть» объектов. К этой группе шкал относится большинство шкал, используемых в социологических и психологических исследованиях. Частным случаем шкал порядка являются балльные шкалы, используемые в практике спортивного судейства или оценок знаний в школе. Если, скажем, по некоторой дисциплине два студента имеют оценки «отлично» и «удовлетворительно», то можно лишь утверждать, что уровень подготовки по этой дисциплине первого студента выше (больше), чем второго, но нельзя сказать, на сколько или во сколько раз больше.
Оказывается, что в таких случаях проблема оценки тесноты связи разрешима, если упорядочить, или ранжировать, объекты анализа по степени выраженности измеряемых признаков. При этом каждому объекту присваивается определенный номер, называемый рангом. Например, объекту с наименьшим проявлением (значением) признака присваивается ранг 1, следующему за ним – ранг 2 и т.д. Объекты можно располагать и в порядке убывания проявления (значений) признака. Если объекты ранжированы по двум признакам, то имеется возможность оценить тесноту связи между признаками, основываясь на рангах, т.е. тесноту ранговой корреляции.
В дополнение к (5.2) в этой шкале необходимо добавить следующие аксиомы - аксиомы упорядоченности:
| Шкала простого порядка | Шкала слабого порядка |
4. Если 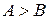 , то , то 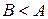
| 4̽. Либо 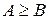 , либо , либо 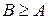
|
5. Если 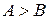 , и , и 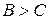 , то , то 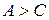
| 5̽. Если 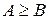 , и , и 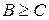 , то , то 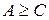 . .
|
Существует ещё шкала частичного порядка. «Частичный порядок» часто встречается при оценке субъективных предпочтений.
Примеры шкалы порядков:
1) Более длинный отпуск предпочтительнее уменьшения рабочего дня на полчаса. Уменьшение рабочего дня на полчаса предпочтительнее повышения зарплаты на 500 р. Но необязательно более длинный отпуск предпочтительнее повышения зарплаты на 500 р.
2) Что лучше: клетчатые шарфы или семискоростные миксеры; чтение литературы или прослушивание музыкальных записей.
3) Шкала твёрдости по Моору (1811 г.): из двух минералов твёрже тот, который оставляет на другом царапины или вмятины при достаточно сильном соприкосновении. Эталоны: 1 – тальк, 2 – гипс, 3 – кальций, 4 – флюорит, 5 – апатит, 6 – ортоклаз, 7 – кварц, 8 – топаз, 9 – корунд, 10 – алмаз.
4) Шкала силы ветра по Бофорту (1806 г.). Сила ветра определяется по волнению моря: 0 – штиль, 4 – умеренный ветер, 6 – сильный ветер, 10 – шторм (буря), 12 – ураган.
5) Балльные шкалы оценки знаний учащихся.
Отметим, что отношение порядка ничего не говорит о дистанции между сравниваемыми классами. Поэтому порядковые экспериментальные данные, даже если они выражены числами, нельзя рассматривать как числа, например, нельзя вычислять выборочное среднее.
Допустимые операции:
– ранг объёма
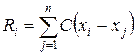 , где , где 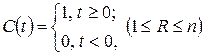 . .
| (5.3) |
Ранги можно присваивать по старшему в группе одинаковых, по среднему, либо случайным образом.
– выборочная медиана, т.е. наблюдение с рангом 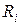 , ближайшее к
, ближайшее к 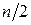 ;
;
– выборочные квантили любого уровня 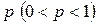 , т.е. наблюдение с рангом
, т.е. наблюдение с рангом 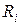 , ближайшим к
, ближайшим к 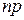 ;
;
– коэффициенты корреляции: 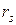 - Спирмена,
- Спирмена, 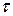 - Кендалла.
- Кендалла.
Коэффициент ранговой корреляции Спирмена находится по формуле:
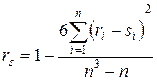 . .
| (5.4) |
где 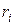 и
и 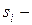 ранги
ранги 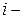 го объекта по переменным
го объекта по переменным 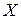 и
и 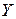 ,
, 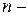 число пар наблюдений.
число пар наблюдений.
Если ранги всех объектов равны ( 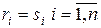 ), то
), то 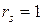 , т.е. при полной прямой связи
, т.е. при полной прямой связи 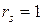 . При полной обратной связи, когда ранги объектов по двум переменным расположены в обратном порядке, можно показать, что
. При полной обратной связи, когда ранги объектов по двум переменным расположены в обратном порядке, можно показать, что 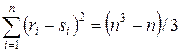 и по формуле (5.4)
и по формуле (5.4) 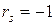 . Во всех остальных случаях
. Во всех остальных случаях 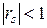 .
.
Коэффициент ранговой корреляции Кендалла находится по формуле:
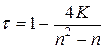 . .
| (5.5) |
Для определения 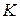 необходимо ранжировать объекты по одной переменной в порядке возрастания рангов и определить соответствующие их ранги (
необходимо ранжировать объекты по одной переменной в порядке возрастания рангов и определить соответствующие их ранги ( 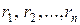 ) по другой переменной. Статистика
) по другой переменной. Статистика 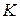 равна общему числу инверсий (нарушений порядка, когда большее число стоит слева от меньшего) в ранговой последовательности (ранжировке)
равна общему числу инверсий (нарушений порядка, когда большее число стоит слева от меньшего) в ранговой последовательности (ранжировке) 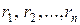 . При полном совпадении двух ранжировок имеем
. При полном совпадении двух ранжировок имеем 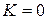 и
и 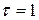 ; при полной противоположности можно показать, что
; при полной противоположности можно показать, что 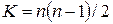 и
и 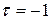 . Во всех остальных случаях
. Во всех остальных случаях 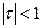 .
.
5.4. Шкала интервалов.
Шкала интервалов, в которой можно менять как начало отсчёта, так и единицы измерения. Если упорядочивание объектов можно выполнить настолько точно, что известны расстояния между любыми двумя из них, то измерение оказывается значительно сильнее, чем в шкале порядка. Естественно выражать все измерения в единицах, хотя и произвольных, но одинаковых по всей длине шкалы. Следствием такой равномерности шкал этого класса является независимость отношения двух интервалов от того, в какой из шкал эти интервалы измерены (т.е. какова единица длины и какое значение принято за начало отсчёта).
Если в одной шкале измеренные интервалы равны 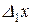 и
и 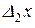 , а во второй –
, а во второй – 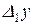 и
и 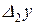 , то справедливо соотношение:
, то справедливо соотношение: 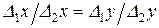 .
.
В этой шкале только интервалы могут иметь смысл настоящих чисел, допускающих математические действия с ними. Примерами шкал интервалов могут быть шкалы для измерения температуры (Цельсия, Кельвина (К = 273 + С), Фаренгейта (F = 5/9C + 32)), давления, промежутков времени и т.п.
Допустимые операции – определение интервала между двумя измерениями. Над интервалами – любые арифметические или статистические операции.
5.5. Шкала отношений.
Шкала отношений, в которой начало отсчёта неизменно, а единицы измерения можно изменять (масштабировать). К предыдущим пяти аксиомам необходимо добавить еще четыре.
Аксиомы аддитивности:
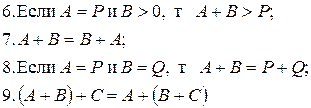
| (5.6) |
Измерения в этой шкале являются полноправными числами, с ними можно выполнять любые арифметические действия. Этот класс шкал обладает следующей особенностью: отношение двух наблюдаемых значений измеряемой величины не зависит от того, в какой из шкал произведены измерения, т.е. 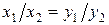 .
.
Примерами шкал отношений являются шкалы для измерения веса, длины и т.п.
5.6. Абсолютная шкала.
Абсолютная шкала, результатом измерения в которой является число, выражающее количество элементов в множестве. В данной шкале начало отсчёта и единицы измерения неизменны. Числа, полученные по такой шкале, можно складывать, вычитать, делить, умножать – все эти действия будут осмысленными. Из перечисленных шкал абсолютная шкала является самой «сильной», а номинальная – самой «слабой». Действительно, из абсолютных данных можно узнать всё то, что могут дать любые другие шкалы, но не наоборот.
Пример. Из того, что в группе А – 15 студентов, в группе В – 20, а в группе С – 30, можно узнать:
в А студентов в 2 раза меньше, чем в С (шкала отношений);
в В студентов на 10 человек меньше, чем в С (шкала интервалов);
в А студентов просто меньше, чем в В и С (шкала порядка);
в А, В, С студентов не одно и то же количество (шкала наименований).
Использовать только абсолютные шкалы не всегда целесообразно. Для получения информации о свойствах, измеряемых в сильных шкалах, требуются более совершенные (сложные, дорогие) измерительные приборы и процедуры. К тому же, таких приборов и процедур для измерения многих характеристик просто нет. Например, можно выяснить, чего данному человеку хочется больше – чая или кофе, но определить, насколько больше или во сколько раз, затруднительно.
В зависимости от существа или важности того или иного фактора на этапе подготовки и принятия решений могут быть использованы различные шкалы. В таблице приведены типы шкал и их основные характеристики.
Дата добавления: 2016-03-05; просмотров: 3599;
