Алгоритмы многокритериальной оптимизации.
4.1. Множество Парето.
Несмотря на ряд существенных трудностей, связанных с неопределенностью, мы до сих пор рассматривали только самые простые случаи, когда ясен критерий, по которому производится оценка эффективности, и требуется обратить в максимум (минимум) один-единственный показатель 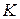 . К сожалению, на практике такие задачи, где критерий оценки однозначно диктуется целевой направленностью операции, встречаются не так уж часто. Когда идет речь о крупномасштабных, сложных операциях, эффективность, как правило, не может быть полностью охарактеризована с помощью одного-единственного показателя
. К сожалению, на практике такие задачи, где критерий оценки однозначно диктуется целевой направленностью операции, встречаются не так уж часто. Когда идет речь о крупномасштабных, сложных операциях, эффективность, как правило, не может быть полностью охарактеризована с помощью одного-единственного показателя 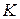 . На практике часто возникает ситуация, когда эффективность операции приходится оценивать не по одному, а сразу по нескольким критериям
. На практике часто возникает ситуация, когда эффективность операции приходится оценивать не по одному, а сразу по нескольким критериям 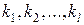 . Такие задачи исследования операций называются многокритериальными. Главной особенностью этой ситуации является то, что требования ко всем показателям несовместимы или противоречивы. Как правило, требование
. Такие задачи исследования операций называются многокритериальными. Главной особенностью этой ситуации является то, что требования ко всем показателям несовместимы или противоречивы. Как правило, требование 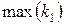 не обращает ни в максимум ни в минимум другие критерии
не обращает ни в максимум ни в минимум другие критерии 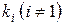 . Для сравнения векторов
. Для сравнения векторов 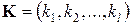 удобно привести все показатели к стандартному, чтобы все критерии минимизировались и чтобы они имели безразмерный масштаб. Векторный критерий считается стандартным, если он удовлетворяет условию
удобно привести все показатели к стандартному, чтобы все критерии минимизировались и чтобы они имели безразмерный масштаб. Векторный критерий считается стандартным, если он удовлетворяет условию 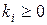 , и чем меньше
, и чем меньше 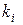 , тем лучше операция (система). Таким образом, идеальной считается система, у которой
, тем лучше операция (система). Таким образом, идеальной считается система, у которой 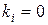 . Полностью идеальной системе соответствует
. Полностью идеальной системе соответствует 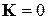 .
.
Прежде всего, анализ векторов позволяет заранее отбросить явно нерациональные варианты решений, уступающие лучшим вариантам по всем показателям. Пусть имеется многокритериальная задача исследования операций с 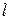 критериями
критериями 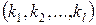 . Для простоты предположим, что все эти величины желательно максимизировать. Пусть в составе множества возможных решений есть две альтернативы
. Для простоты предположим, что все эти величины желательно максимизировать. Пусть в составе множества возможных решений есть две альтернативы 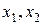 такие, что все критерии
такие, что все критерии 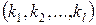 для первого решения больше или равны соответствующим критериям для второго решения, причем хотя бы один из них действительно больше. Очевидно, тогда в составе множества альтернатив
для первого решения больше или равны соответствующим критериям для второго решения, причем хотя бы один из них действительно больше. Очевидно, тогда в составе множества альтернатив 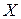 нет смысла сохранять решение
нет смысла сохранять решение 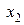 , оно вытесняется (или, как говорят, «доминируется») решением
, оно вытесняется (или, как говорят, «доминируется») решением 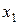 . Ладно, выбросим решение
. Ладно, выбросим решение 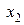 как неконкурентоспособное и перейдем к сравнению других альтернатив по всем критериям. В результате такой процедуры отбрасывания заведомо непригодных, невыгодных решений множество
как неконкурентоспособное и перейдем к сравнению других альтернатив по всем критериям. В результате такой процедуры отбрасывания заведомо непригодных, невыгодных решений множество 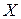 обычно сильно уменьшается: в нем сохраняются только так называемые эффективные решения, характерные тем, что ни для одного из них не существует доминирующего решения.
обычно сильно уменьшается: в нем сохраняются только так называемые эффективные решения, характерные тем, что ни для одного из них не существует доминирующего решения.
Определение. Множество, в котором ни для одного из элементов не существует доминирующего решения называется множеством Парето.
Так как множество Парето, как правило, содержит более чем одну альтернативу, то для получения единственного решения необходимо применить дополнительные принципы оптимальности (условия согласования критериев).
Проиллюстрируем прием выделения паретовских решений на примере задачи с двумя критериями: 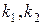 (оба требуется максимизировать). Множество
(оба требуется максимизировать). Множество 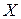 состоит из конечного числа
состоит из конечного числа 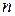 возможных решений
возможных решений 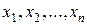 . Каждому решению соответствуют определенные значения показателей
. Каждому решению соответствуют определенные значения показателей 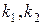 ;будем изображать решение точкой на плоскости с координатами
;будем изображать решение точкой на плоскости с координатами 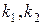 и занумеруем точки соответственно номеру решения (рис.7).
и занумеруем точки соответственно номеру решения (рис.7).
 Очевидно, из всего множества
Очевидно, из всего множества 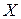 эффективными будут только решения
эффективными будут только решения 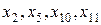 ,лежащие на правой верхней границе области возможных решений. Для всякого другого решения существует хотя бы одно доминирующее, для которого либо
,лежащие на правой верхней границе области возможных решений. Для всякого другого решения существует хотя бы одно доминирующее, для которого либо 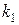 ,либо
,либо 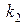 ,либо оба больше, чем для данного. И только для решений, лежащих на правой верхней границе, доминирующих не существует.
,либо оба больше, чем для данного. И только для решений, лежащих на правой верхней границе, доминирующих не существует.
Когда из множества возможных решений выделены эффективные, «переговоры» могут вестись уже в
Рис. 7 пределах этого «эффективного» множества. На рис. 7 его образуют четыре решения: 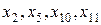 . Из них
. Из них 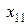 – наилучшее по критерию
– наилучшее по критерию 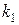 ,
, 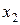 – по критерию
– по критерию 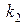 . Дело лица, принимающего решение, выбрать тот вариант, который для него предпочтителен и «приемлем» по обоим критериям.
. Дело лица, принимающего решение, выбрать тот вариант, который для него предпочтителен и «приемлем» по обоим критериям.
Аналогично строится множество эффективных решений и в случае, когда показателей не два, а больше (при числе их, большем трех, геометрическая интерпретация теряет наглядность, но суть дела сохраняется). Множество эффективных решений легче обозримо, чем множество 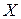 .
.
4.2. Методы оптимизации на множестве Парето.
После нахождения множества Парето, если количество альтернатив в нем больше двух, встает вопрос о выборе единственного решения. Так как альтернативы на множестве Парето обладают таким свойством, что каждая из них лучше по одному критерию, но хуже по другому, то объективно предпочесть одну из альтернатив невозможно. Поэтому необходимо выбрать некоторую схему компромиссов для всей совокупности критериев. Далее представлены несколько методов решения задач многоцелевого программирования. Все методы основаны на сведении множества частных целей к одной целевой функции. Эти методы различны по своей природе и в общем случае дают оптимальные решения, не совпадающие между собой. Вместе с тем нельзя сказать, что один из этих методов лучше другого; в сущности, они предназначены для решения задач с разными предпочтениями в процессе принятия решений.
Принцип равенства критериев.
В этом случае считается, что оптимальной является альтернатива из множества Парето, при которой все критерии, приведенные к стандартной форме ( 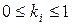 ), равны.
), равны.
Принцип равного влияния.
Здесь оптимальной считается альтернатива множества Парето, при которой
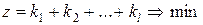 . .
| (4.1) |
По сути это точка касания данной гиперплоскости с множеством Парето.
Метод весовых коэффициентов.
В методе весовых коэффициентов единственная целевая функция формируется как взвешенная сумма исходных частных целевых функций.
Предположим, что модель целевого программирования имеет 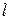 целей следующего вида
целей следующего вида
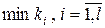 . .
| (4.2) |
В методе весовых коэффициентов обобщенная целевая функция определяется следующим образом
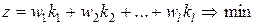 . .
| (4.3) |
Здесь 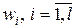 – положительные весовые коэффициенты, которые отображают предпочтения, отдаваемые каждой цели. Например, вариант
– положительные весовые коэффициенты, которые отображают предпочтения, отдаваемые каждой цели. Например, вариант 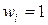 для всех i говорит о равнозначности всех целей. Чем больше вес компоненты критерия, тем большее влияние оказывает этот критерий. Задание значений весовым коэффициентам очень субъективно. Однако, набирая статистику по результатам выбора, можно, например, разумным образом подобрать значения «весов»
для всех i говорит о равнозначности всех целей. Чем больше вес компоненты критерия, тем большее влияние оказывает этот критерий. Задание значений весовым коэффициентам очень субъективно. Однако, набирая статистику по результатам выбора, можно, например, разумным образом подобрать значения «весов» 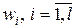 в формуле (3.25), в общем случае зависящих как от условий, так и самих показателей
в формуле (3.25), в общем случае зависящих как от условий, так и самих показателей 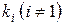 , и воспользоваться таким обобщенным критерием для выбора решения, на этот раз уже автоматического, без участия человека. На это иногда приходится идти в случаях, когда времени на обдумывание компромиссного решения нет (например, в условиях боевых действий), или же в случае, когда выбор решения передается автоматизированной системе управления (АСУ).
, и воспользоваться таким обобщенным критерием для выбора решения, на этот раз уже автоматического, без участия человека. На это иногда приходится идти в случаях, когда времени на обдумывание компромиссного решения нет (например, в условиях боевых действий), или же в случае, когда выбор решения передается автоматизированной системе управления (АСУ).
Метод приоритетов.
В этом методе сначала целевые функции ранжируются в порядке их важности, так как их оценивает специалист по принятию решений. Далее поочередно решаются задачи с одной целевой функцией, начиная с задачи с целевой функцией 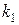 , имеющей наивысший приоритет, и заканчивая задачей с целевой функцией
, имеющей наивысший приоритет, и заканчивая задачей с целевой функцией 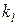 , имеющей минимальный приоритет. В процессе решения последовательных задач решение задачи с целевой функцией, имеющей более низкий приоритет, не должно ухудшать полученные ранее решения задач с целевыми функциями, имеющими более высокий приоритет. Это означает, что если
, имеющей минимальный приоритет. В процессе решения последовательных задач решение задачи с целевой функцией, имеющей более низкий приоритет, не должно ухудшать полученные ранее решения задач с целевыми функциями, имеющими более высокий приоритет. Это означает, что если 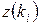 – оптимальное значение целевой функции
– оптимальное значение целевой функции 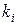 , то для всех
, то для всех 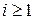 оптимизация любой целевой функции
оптимизация любой целевой функции 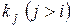 с меньшим приоритетом не может ухудшить значение
с меньшим приоритетом не может ухудшить значение 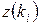 . Для этого все показатели эффективности
. Для этого все показатели эффективности 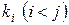 , переводятся в разряд ограничений на достигнутом ранее уровне. Варианты решения, не укладывающиеся в заданные границы, сразу же отбрасываются как недопустимые.
, переводятся в разряд ограничений на достигнутом ранее уровне. Варианты решения, не укладывающиеся в заданные границы, сразу же отбрасываются как недопустимые.
Метод последовательных уступок.
Этот метод аналогичен предыдущему. Сначала ищется решение, обращающее в максимум первый (важнейший) показатель 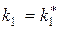 , но исходя из практических соображений и точности исходных данных, назначается некоторая «уступка»
, но исходя из практических соображений и точности исходных данных, назначается некоторая «уступка» 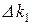 , которую мы согласны сделать для того, чтобы максимизировать второй критерий показатель
, которую мы согласны сделать для того, чтобы максимизировать второй критерий показатель 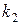 . Наложим на показатель
. Наложим на показатель 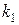 ограничение: потребуем, чтобы он был не меньше, чем
ограничение: потребуем, чтобы он был не меньше, чем 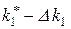 ,и при этом ограничении ищем решение, обращающее в максимум
,и при этом ограничении ищем решение, обращающее в максимум 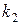 . Далее снова назначим «уступку» в
. Далее снова назначим «уступку» в 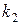 ,ценой которой можно максимизировать
,ценой которой можно максимизировать 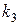 ,и т. д. Такой способ построения компромиссного решения хорош тем, что здесь сразу видно, ценой какой «уступки» в одном показателе приобретается выигрыш в другом, и какова величина этого выигрыша. Заметим, что иногда даже при малом
,и т. д. Такой способ построения компромиссного решения хорош тем, что здесь сразу видно, ценой какой «уступки» в одном показателе приобретается выигрыш в другом, и какова величина этого выигрыша. Заметим, что иногда даже при малом 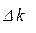 можно достичь существенного улучшения других критериев.
можно достичь существенного улучшения других критериев.
Следует отметить, что в приведенных методах используется процедура упорядочения критериев по их важности. Эта самостоятельная проблема является не до конца формализованной, и окончательный выбор решения всегда определяется волевым актом или на основе метода экспертных оценок.
Прежде чем перейти к методу экспертных оценок, рассмотрим типы измерительных шкал, которыми руководствуются эксперты в своих оценках.
Дата добавления: 2016-03-05; просмотров: 1062;
