Центробежный момент инерции.

ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ.

Статический момент.

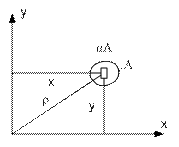
Статическим моментом плоской фигуры называется сумма произведений элементарных площадок на их координаты до соответствующей оси:

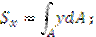
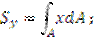
Измеряют в единицах длины в третьей степени, может быть положительным «+», отрицательным «-» и равным нулю.

Для сложной фигуры находится по формулам:

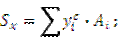
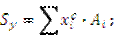
где 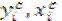– координаты центров тяжести отельных простых фигур.

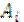– площади этих фигур.

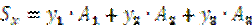= у_с∙А_і

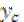– координата центра тяжести всей фигуры,

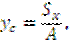
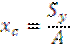– положение центра тяжести сложной фигуры.

Моменты инерции плоских сечений.

Осевым (экваториальным) моментом инерции плоской фигуры называют сумму произведений элементарных площадок на квадраты их расстояний до соответствующей оси.

Может быть положительным, измеряется в единицах длины в четвертой степени.

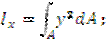
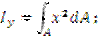
Полярный момент инерции.

J_ρ = ∫_А ρ² dA_і Может быть положительным, измеряется в единицах длины в 4 степени.

где 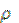- полярная координата,

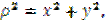
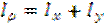
Центробежный момент инерции.

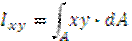
Может быть положительным, отрицательным и равным 0, измеряется в единицах длины в 4 степени.

Формула перехода для моментов инерции при параллельном переносе осей.

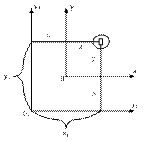
Пусть J и J_y известны. Надо найти J_x1 и J_y1 относительно осей Х₁ и У₁, отстоящих на расстояниях а и b от осей и У.

По рисунку: X₁=x+b; y₁=y+a

J_Х1=J_x+2∙a∙S_x+a²∙A

J_У1=J_y+2∙b∙S_y+b²∙A - формулы перехода для любых осей.

Если оси Х и У проходят через центр тяжести сечения, то S_x=S_y=0

J_Х1=J_x+ a²∙A J_У1=J_y+ b²∙A - формулы перехода для моментов инерциипри

параллельном переносе осей (от Х к Х₁ ; от У к У₁), когда оси Х и У центральные.

Для центробежного момента инерции:

J_Х1У1=J_xy+a∙b∙A (если оси Х и У центральные оси).

А в общем случае для любых осей: J_X1У1=J_xу+a∙S_x+ b∙S_y + a∙b∙A

Моменты инерции некоторых фигур.

а) прямоугольное

Относительно центральных осей:

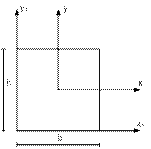
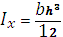
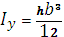Относительно осей Х1 и У1:

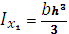
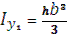
б) треугольное

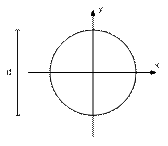
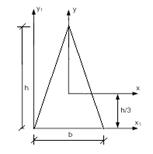в) круглое

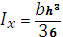
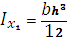
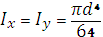
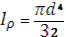
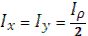
г) кольцевое

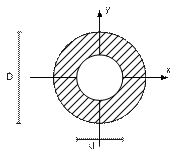
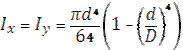
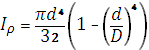
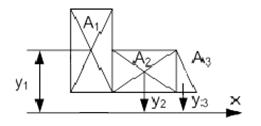
д) Момент инерции сложной фигуры равен сумме моментов инерции ее составляющих частей.

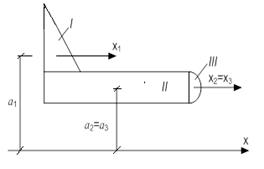
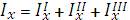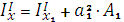где , А1 - площадь первой фигуры; Jx II и Jx III - находятся аналогично.

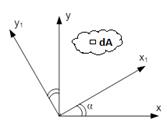
Формулы перехода для моментов инерции при повороте осей.

При повороте осей на угол α используются формулы:

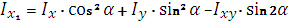
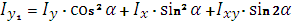
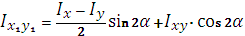
Главные оси инерции и главные моменты инерции.

Оси, относительно которых моменты инерции принимают экстремальные значения, называют главными.

Угол наклона главных осей вычисляют по формуле: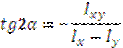

Главные моменты инерции вычиcляют по формулам:

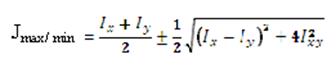
J_xy=0 – центробежный момент относительно главных осей равен нулю.

Графическое определение моментов инерции.

Дано: 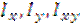– известны, где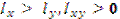

Надо найти: 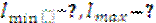, α -? – угол наклона главных осей.

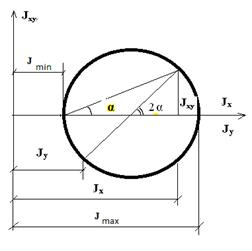
Решение: Путем графических построений можно найти требуемые величины. Откладывают 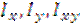, рисуют круг и проводят остальные линии. После построений получаем искомые величины в масштабе.

Радиус инерции

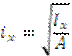
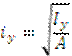
Если Х и У - центральные оси, то радиус инерции называется главным.

Эллипс инерции.

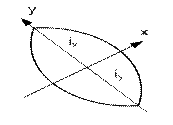
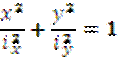- уравнение эллипса