Напряжения в наклонных сечениях при осевом растяжении или сжатии.

СЛОЖНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ.

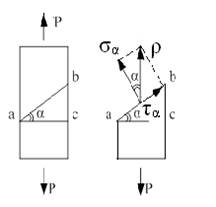
При осевом растяжении (или сжатии) определяем напряжение на площадке ab, наклоненной под углом α. Отбросим мысленно верхнюю часть стержня и рассмотрим равновесие нижней. Площадь сеч (а с) – обозначим А Площадь сеч (а b) – обозначим Аα 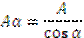  ρ =Р/ Аα=(Р/ А) соs α= σ соs α, где σ=Р/ А – напряжение на площадке a с

Разложим напряжение ρ на σ_α и τ_α :

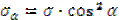
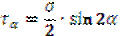
При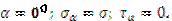

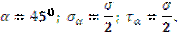
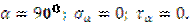
Вывод: наибольшие касательные напряжения возникают при α=45°: τ_max =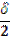

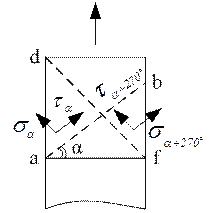
Напряжения на площадке df перпендикулярной площадке ab:

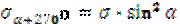
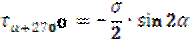
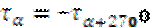- закон парности касательных напряжений.

Вывод: во взаимно перпендикулярных площадках касательные напряжения равны по величине но противоположны по знаку - закон парности касательных напряжений.

Понятие о главных напряжениях.

Площадки, в которой отсутствуют τ называются главными площадками, а нормальные напряжения, действующие по ним называются главными нормальными напряжениями.

Вывод: таким образом, при осевом растяжении и сжатии главными являются площадки перпендикулярные и параллельные оси стержня.

Примечание: в любом теле имеется три взаимно перпендикулярных площадки, в которых τ=0

Различают три напряженных состояния:

1 Линейное напряженное состояние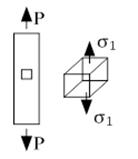
2. Плоское напряженное состояние   3. Объемное напряженное состояние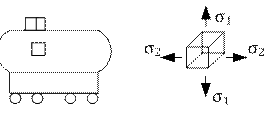

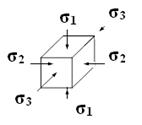
Напряжение в наклонных сечениях при осевом растяжении и сжатии по двум взаимно перпендикулярным направлениям.

Известны: σ₁ , σ₂.

Необходимо определить σ_{φ и} τ_φ на наклонной площадке.

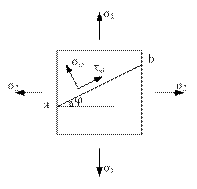
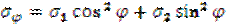
Полные напряжения на наклонной площадке находятся суммированием напряжений от σ1 и σ2 : 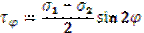Вывод:

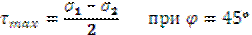
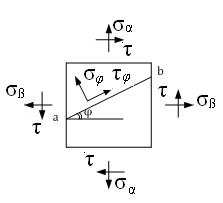
Определение главных напряжений.

Известны: σ_α , σ_β , τ .

Необходимо определить σ_{φ и} τ_φ на наклонной площадке и главные напряжения.

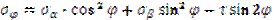
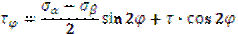
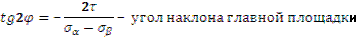Главные напряжения определяются:

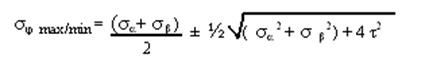
Графическое определение напряжений Круг Отто-Мора.

Дано: 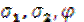. Определить напряжение на наклонной площадке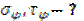

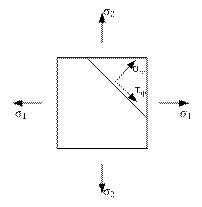
Решение: Путем графических построений можно найти требуемые величины и их направление. Откладывают σ1 и σ2 , рисуют круг, от центра круга откладывают 2φ и остальные линии. 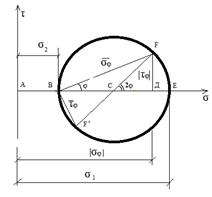После построений получаем: FD= │τφ│ AD=│σφ│

Если направление σ₁ совместить с осью σ, то линия ВF покажет направление напряжения

σ_φ, а линия BF₁ совпадет с направлением τ_φ.

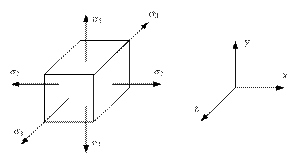
Обобщенный закон Гука.

	Выделим из тела элемент, работающий в условиях объемного напряженного состояния. Если элемент испытывает напряжение только в одном направлении, вдоль оси y, то деформации будут только от 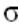1. По закону Гука деформации будут определяться по формуле: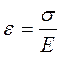

А по перпендикулярным направлениям: - вдоль оси Х₁

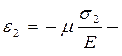- вдоль оси Х_2. Тогда все деформации от σ_{1 ,} σ_{2 ,} σ₃

можно представить в виде таблицы:

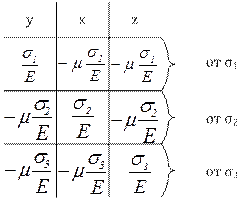
На основании принципа независимости действия сил относительные деформации по осям x, y, z будут определяться по формулам:

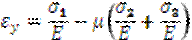
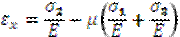
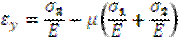
– обобщенный закон Гука

Объемная деформация.

Дан кубик с ребром равным 1.

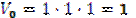– объем до деформации.

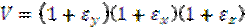– объем после деформации.

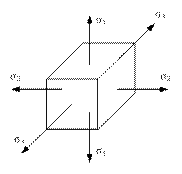
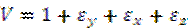
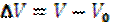
Пренебрегая бесконечно малыми величинами второго и третьего порядка получим: 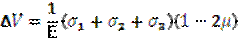– приращение объема кубика. при .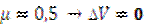

Гипотезы прочности.

При осевом растяжении и сжатии прочность можно проверить опытным путем. Если же имеется сложное напряженное состояние, то прочность будет зависеть от трех составляющих напряжений σ_1,σ₂ σ₃, которые имеют многообразие сочетаний.

Учитывая сложность постановки таких опытов, для оценки прочности принимаются гипотезы или теории прочности.

1) Теория наибольших нормальных напряжений (предложил Галилей): согласно ей предельное состояние материала возникает, когда наибольшее напряжение достигает величины, при которой появляются пластические деформации или разрушение в случае одноосного напряженного состояния.

σ₁≤ 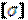, где σ₁>σ₂>σ₃

При этом σ₂ и σ₃ во внимание не принимаются.

Гипотеза применима для хрупких материалов.

2) Гипотеза наибольших линейных деформаций (предложил Мориот).

Согласно ей условие прочности имеет вид:

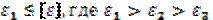
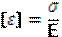
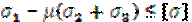
В этой гипотезе учитываются все три напряжения и она применима для пластичных материалов.

3) Теория наибольших касательных напряжений (третья теория)

Предполагает, что независимо от напряженного состояния 2 тела являются равнопрочными, если наибольшие касательные напряжения в них одинаковы.

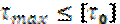
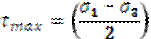- при сложном напряженном состоянии.

τ_{о =} σ_оп / 2 - при линейном напряженном состоянии.

σ₁- σ_{3 ≤} σ_оп

Эта теория применима для пластичных материалов.

4) Энергетическая теория

Удельная потенциальная энергии деформации:

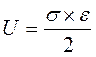- удельная потенциальная энергии деформации при линейном напряженном состоянии.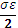

При сложном напряженном состоянии:

U_v = [σ₁²+ σ₂²+ σ₃² -2μ×((σ₁×σ₂)+( σ₂×σ₃)+( σ₁×σ₃))]/2Е

При µ=0,5:

U= [σ₁²+ σ₂²+ σ₃² - σ₁×σ₂- σ₂×σ₃- σ₁×σ₃]/2Е

Энергетическая теория основывается на предположении о том, что количество удельной потенциальной энергии изменения формы, накопленной к моменту наступления предельного состояния одинаково как при сложном напряженном состоянии, так и при простом растяжении.

U_ф≤[U_фо]

U_ф – расчетная величина энергии, связанной с изменением формы кубика с ребром равным 1 при исследуемом напряженном состоянии.

[U_фо] – предельное значение энергии, полученное из опыта на простое растяжение.

Полная энергия: U= U_v + U_ф, где

U_v – потенциальная энергия затраченная на изменение объема;

U_ф – потенциальная энергия затраченная на изменение формы тела.

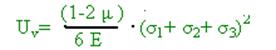- удельная потенциальная энергии изменения объема.

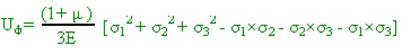- удельная потенциальная энергии изменения формы.

При σ₁=σ₂=0 получим: [U_ф] 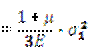- удельная потенциальная энергии изменения формы при линейном напряженном состоянии.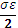

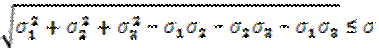- энергетическая теория

Для пластичных материалов теория дает хорошие результаты.

5) Теория прочности Мора (изучить самостоятельно)