Оценка срочных аннуитетов

Аннуитет представляет собой частный случай денежного потока, а именно, по это поток, в котором денежные поступления в каждом периоде одинаковые величине. Если число равных временных интервалов ограничено, аннуитет называется срочным. В этом случае:

C₁= C₂= ··· =C_n= A

Как и в общем случае, выделяют два типа аннуитетов: постнумерандо и пренумерандо (рис. 4.10) .

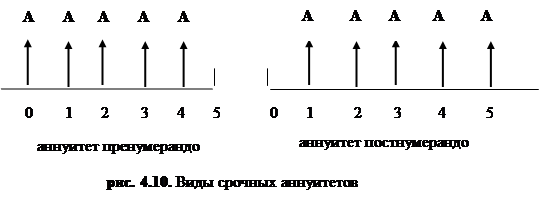Примером срочного аннуитета постнумерандо могут служить регулярно поступающие рентные платежи за пользование сдан­ным в аренду земельным участком в случае, если договором предусматривается регулярная оплата аренды по истечении оче­редного периода. В качестве срочного аннуитета пренумерандо выступает, например, схема периодических денежных вкладов на банковский счет в начале каждого месяца с целью накопления достаточной суммы для крупной покупки.

Для оценки будущей и приведенной стоимости аннуитета можно пользоваться рассмотренными в п.4.5 вычислительными формулами, вместе с тем благодаря специфике аннуитетов в отношении равенства денежных поступлений эти формулы могут быть существенно упрощены.

Прямая задача оценки срочного аннуитета при заданных ве­личинах регулярного поступления (А) и процентной ставке (r) предполагает оценку будущей стоимости аннуитета. Как следует из логики, присущей схеме аннуитета, наращенный денежный поток имеет вид:

A , A·(1+r) , A· (1+r)² ,…, A· (1+r) ^n-1 ,

а формула (4.15) трансформируется следующим образом:

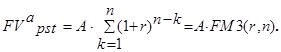(4.20)

Входящий в формулу мультиплицирующий множитель 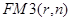представляет собой сумму членов геометрической про­грессии:

S=1·+ q + q²+ ··· + q^n-1,

где q =1 – r (q≠1).

Умножив обе части этого уравнения на q, получим:

q· S=q + q²+ ··· + q^n-1+ qⁿ .

Вычтя одно уравнение из другого, получим

S – q S=1– qⁿ .

Таким образом,

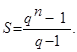
Отсюда находим, что

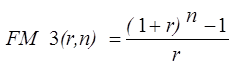(4.21)

Экономический смысл мультиплицирующего множителя FM3(r,n)заключается в следующем: он показывает, чему будет равна суммарная величина срочного аннуитета в одну денежную единицу (например, один рубль) к концу срока его действия. Предполагается, что производится лишь начисление денежных сумм, а их изъятие может быть сделано по окончании срока действия аннуитета. Множитель FM3(r,n)часто используется в финансовых вычислениях, и поскольку легко заметить, что его значения в общем виде зависят лишь от r и n, их можно табулировать. Значения множителей для различных сочетаний r и n приведены в приложении 3.

Пример

Вам предлагают сдать в аренду участок на три года и выбрать один из двух вариантов оплаты аренды: а) 10 млн.руб. в конце каждого года; б) 35 млн.руб. в конце трехлетнего периода. Какой вариант более предпочтителен, если банк предлагает 20% годовых по вкладам ?

Первый вариант оплаты как раз и представляет собой анну­итет постнумерандо при n = 3 и А = 10 млн. руб. В этом случае имеется возможность ежегодного получения арендного платежа и инвестирования полученных сумм как минимум на условиях 20% годовых (например, вложение в банк). К концу трехлетнего периода накопленная сумма может быть рассчитана в соответст­вии со схемой, аналогичной схеме, представленной на рис. 4.6.

FV = A·FM3(20%, 3) = 10 · 3,640 = 36,4 млн.руб.

Таким образом, расчет показывает, что вариант (а) более выгоден.

Общая постановка обратной задачи оценки срочного анну­итета постнумерандо также достаточно наглядна. В этом случае производится оценка будущих денежных поступлений с позиции текущего момента, под которым в данном случае понимается момент времени, с которого начинают отсчитываться равные временные интервалы, входящие в аннуитет. Схема дисконтиро­вания денежного потока на примере вышеприведенной задачи с арендой участка, построенная по аналогии со схемой на рис. 4.7, представлена на рис. 4.11.

Экономический смысл сделанных расчетов состоит в следу­ющем: с позиции текущего момента реальная стоимость данного аннуитета может быть оценена в 21,064 млн. руб.

Общая формула для оценки текущей стоимости срочного аннуитета постнумерандо выводится из базовой формулы (4.16) и имеет вид:

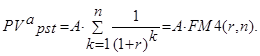(4.22)

Экономический смысл дисконтирующего множителя РМ4(r, n) заключается в следующем: он показывает, чему равна с позиции текущего момента величина аннуитета с регулярными денеж­ными поступлениями в размере одной денежной единицы (напри­мер, один рубль), продолжающегося n равных периодов с задан­ной процентной ставкой r. Значения этого множителя также табулированы (см. приложение 3). В основу расчета табулирован­ных значений дисконтирующего множителя заложена формула:

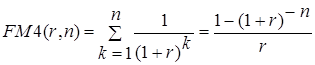(4.23)

Так, для примера, представленного на рис. 4.11:

FM4(20%,3) = 2,106, поэтому: PV^a_pst = 10 • 2,106 = 21,06 млн. руб.

Соответствующие расчетные формулы для аннуитета пренумерандо можно легко вывести из формул (4.18) — (4.23). Так, будущая стоимость аннуитета пренумерандо может быть найдена по формулам:

FV^apre = FV^a pst · (1 +r) = A FM3(r,n)·(1+r). (4.24 )

или

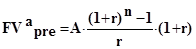(4.25)

Аналогично, приведенная стоимость аннуитета пренумерандо может быть найдена по формулам:

PV^a pre = PV^a pst · (1 + r ) = A FM4(r,n)·(1+r). (4.26 )

или

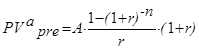(4.27)

Из приведенных формул видно, почему в финансовых табли­цах не уточняется, какая схема подразумевается в финансовой сделке — постнумерандо или пренумерандо; содержание финан­совой таблицы инвариантно к этому фактору. Однако при приме­нении расчетных формул или финансовых таблиц необходимо строго следить за схемой поступления денежных платежей.

Пример

Ежегодно в начале года в банк делается очередной взнос в размере 10 млн.руб. Банк платит 20% годовых. Какая сумма будет на счете по истечении трех лет?

В данном случае мы имеем дело с аннуитетом пренумерандо, будущую стоимость которого и предлагается оценить. В соответ­ствии с формулой (4.24) найдем искомую сумму S:

S = 10 • (1 + 0,2) • FМЗ(20%, 3) = 10 • 1,2 • 3,640 = 43,68 млн. руб.

Многие практические задачи могут быть решены различными способами в зависимости от того, какой денежный поток выделен аналитиком. Рассмотрим простейший пример.

Пример

Вам предложено инвестировать 100 млн.руб. на срок 5 лет при условии возврата этой суммы частями (ежегодно по 20 млн. руб.). По истечении пяти лет выплачивается дополнительно вознаграждение в размере 30 млн. руб. Принимать ли это предложе­ние, если можно «безопасно» депонировать деньги в банк из расчета 12% годовых?

Для принятия решения необходимо рассчитать и сравнить две суммы. При депонировании денег в банк к концу пятилетнего периода на счете будет сумма:

F₅= Р • (1 +r)⁵ = 100 • (1 + 0,12)⁵ = 176 млн. руб.

В отношении альтернативного варианта, предусматривающе­го возмещение вложенной суммы частями, предполагается, что ежегодные поступления в размере 20 млн.руб. можно немедленно пускать в оборот, получая дополнительные доходы. Если нет других альтернатив по эффективному использованию этих сумм, их можно депонировать в банк. Денежный поток в этом случае можно представить двояко:

а) как срочный аннуитет постнумерандо с A = 20, n= 5, r = 20% и единовременное получение суммы в 30 млн. руб.;

б) как срочный аннуитет пренумерандо с A = 20, n = 4, r = 20% и единовременное получение сумм в 20 и 30 млн. руб. В первом случае на основании формулы (4.20) имеем:

S = 20 • FМЗ(12%,5) + 30 = 20 • 6,353 + 30 = 157,06 млн.руб.

Во втором случае на основании формулы (4.24) имеем:

S = 20 · FМЗ(12%,4) · 1,2 + 20 + 30 = 20 × 4,779 × 1,12 + 50 = = 157,06 млн.руб.

Естественно, что оба варианта привели к одинаковому ответу. Таким образом, общая сумма капитала к концу пятилетнего периода будет складываться из доходов от депонирования денег в банке (107,06 млн. руб.), возврата доли от участия в венчурном проекте за последний год (20 млн. руб.) и единовременного вознаграждения (30 млн. руб.). Общая сумма составит, следовате­льно, 157,06 млн.руб. Предложение экономически нецелесообразно.