Оценивание по балльной шкале.
Эксперты оценивают объекты в произвольной балльной шкале. Затем результаты нормируются, т.е. делятся на сумму баллов по всем объектам для конкретного эксперта. После нормировки результаты сводятся в таблицу.
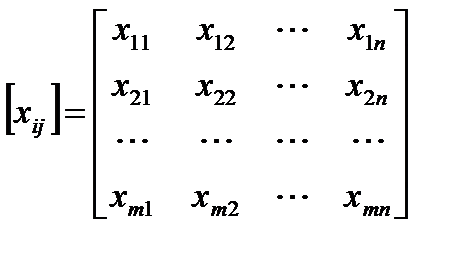 ,
,
где 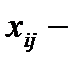 это нормированный балл, присвоенный экспертом
это нормированный балл, присвоенный экспертом 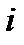 объекту
объекту 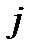 .
.
Нормировка означает, что 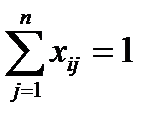 для всех
для всех  .
.
В такой таблице информации больше, чем при ранжировании. Балльная шкала является промежуточной между количественной и порядковой шкалами, поэтому обработку результатов рекомендуется производить дважды:
1) обрабатывать их как количественные данные, используя обычные методы статистики для обработки результатов измерения;
2) обрабатывать методами для порядковых (ранговых) оценок. Предварительно следует перейти к таблице ранжирования.
Если результаты, полученные обоими путями близки друг к другу, то это означает, что полученные выводы основаны на исходной информации, а не на методах ее обработки. Если не совпадают, то следует выяснить причину этого.
При обработке по первому методу обычно используют средний балл:
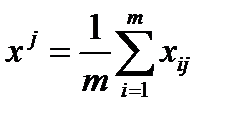 . (8.5)
. (8.5)
Разброс значений для этого объекта характеризуется величиной вариации:
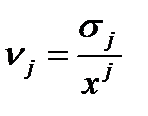 , (8.6)
, (8.6)
где 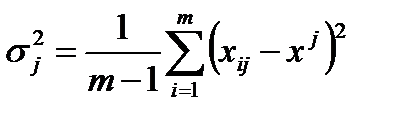 . (8.7)
. (8.7)
Обычно считают, что надежность оценок удовлетворительная, если все 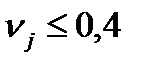 и хорошая, если все
и хорошая, если все 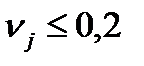 .
.
| Пример 8.2.Четыре эксперта оценили восемь объектов по десятибалльной шкале (
Перейдем к нормированным оценкам:
Результаты вычислений по формулам (8.5) – (8.7) запишем в эту же таблицу. Те же результаты обработаем вторым методом. Для этого перейдем к ранговой шкале.
Число степеней свободы По таблицам (Приложение ) находим Результаты обработки обоими методами совпадают. |
Парные сравнения.
Номер эксперта обозначим 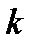 . Эксперт
. Эксперт 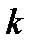 сравнивает каждую пару объектов
сравнивает каждую пару объектов 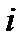 и
и 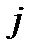 . Его оценка может выражать:
. Его оценка может выражать:
а) просто факт предпочтения объекта 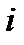 по сравнению с объектом
по сравнению с объектом 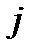 :
: 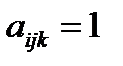 . Если наоборот, то
. Если наоборот, то 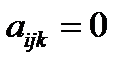 .
.
б) балльную оценку предпочтения: 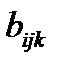 .
.
в) долю суммарной интенсивности предпочтения, приходящуюся на объект 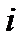 :
: 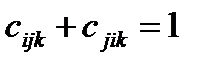 .
.
г) во сколько раз один объект важнее другого: 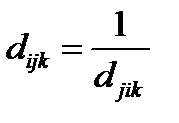 .
.
По результатам экспертизы определяют средние арифметические оценки по всем экспертам:
 : например,
: например, 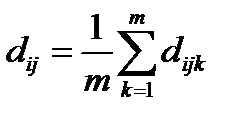 , где
, где 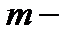 число экспертов.
число экспертов.
Случай а) сводится к случаю в), если трактовать 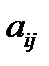 как долю экспертов, предпочитающих объект
как долю экспертов, предпочитающих объект 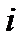 перед объектом
перед объектом 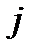 .
.
Случай б) сводится к в) после введения таких оценок: 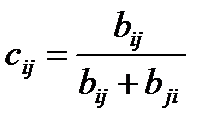 .
.
Случай в) сводится к г) при использовании оценок: 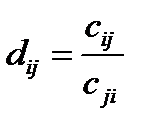 .
.
Поэтому рассмотрим обработку результатов экспертизы применительно к случаю г).
Ясно, что в идеальном случае должно выполняться условие транзитивности:
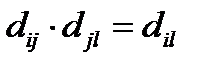 , (8.8)
, (8.8)
в частности 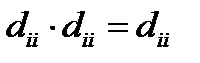 , откуда
, откуда 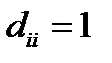 , т.е. в матрице
, т.е. в матрице 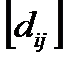 на диагоналях стоят 1.
на диагоналях стоят 1.
Если условие (8.8) выполняется, то существует такой положительный вектор 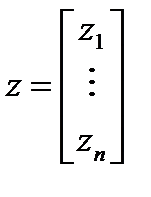 , что
, что 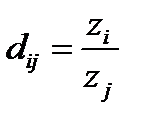 , где
, где 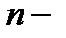 число объектов. Компоненты вектора
число объектов. Компоненты вектора 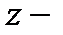 это как-бы идеальные оценки объектов (количественные характеристики ценности или важности объектов).
это как-бы идеальные оценки объектов (количественные характеристики ценности или важности объектов).
Реальная матрица условию (8.8) обычно не удовлетворяет, и ее приходится аппроксимировать идеальной матрицей, используя, например, следующие соображения.
Для идеальной матрицы справедливы равенства для любого 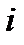 :
:
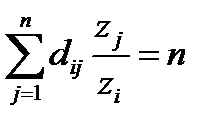 . (8.9)
. (8.9)
Эти равенства можно записать так:
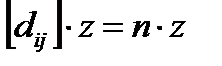 . (8.10)
. (8.10)
Собственный вектор матрицы – это такой, который при умножении на матрицу направления не меняет, а меняет только свою величину. Изменение величины называется собственным числом матрицы. Для идеальной (состоятельной) матрицы собственное число равно 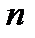 .
.
Для матрицы, удовлетворяющей условию (8.8), число 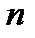 является наибольшим характеристическим числом, а искомый вектор
является наибольшим характеристическим числом, а искомый вектор 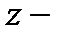 собственным вектором (8.10).
собственным вектором (8.10).
Из теоремы Перрона-Фробениуса следует, что любая матрица 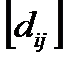 имеет наибольшее характеристическое число
имеет наибольшее характеристическое число 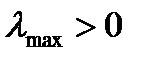 . Поэтому для матрицы, не удовлетворяющей условию (8.8), вектор
. Поэтому для матрицы, не удовлетворяющей условию (8.8), вектор 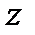 ищется путем решения уравнения:
ищется путем решения уравнения:
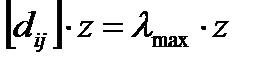 , (8.11)
, (8.11)
причем все компоненты 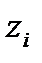 такого вектора обязательно оказываются положительными.
такого вектора обязательно оказываются положительными.
Существуют специальные методы решения уравнения (8.11). Мы воспользуемся итеративным методом, суть которого заключается в последовательном приближении
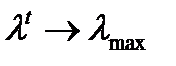 и
и 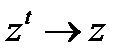 .
.
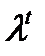 и
и 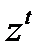 получаются на
получаются на 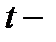 й итерации в соответствии с формулой
й итерации в соответствии с формулой
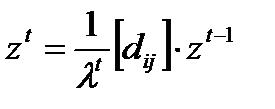 , (8.12)
, (8.12)
где 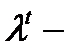 сумма всех компонент вектора
сумма всех компонент вектора 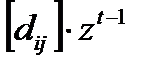 , а в качестве
, а в качестве 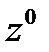 можно взять любой положительный вектор, например,
можно взять любой положительный вектор, например, 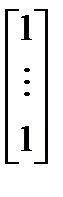 .
.
Итеративный процесс заканчивается, когда вектор 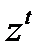 перестает изменяться для заданной точности. Величина
перестает изменяться для заданной точности. Величина 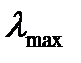 характеризует степень близости матрицы
характеризует степень близости матрицы 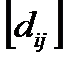 к идеальной (состоятельной), т.е. удовлетворяющей условию (8.8).
к идеальной (состоятельной), т.е. удовлетворяющей условию (8.8).
Пример 8.3.Четыре объекта сравниваются двумя экспертами. Требуется определить коэффициенты важности объектов. Получены следующие результаты:
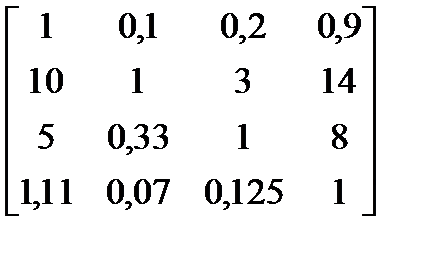 и и 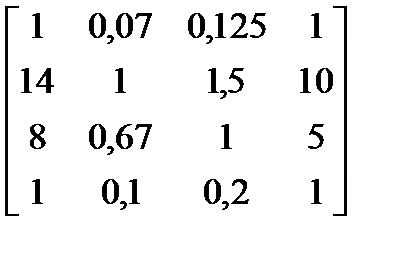 .
Определяем средний балл .
Определяем средний балл 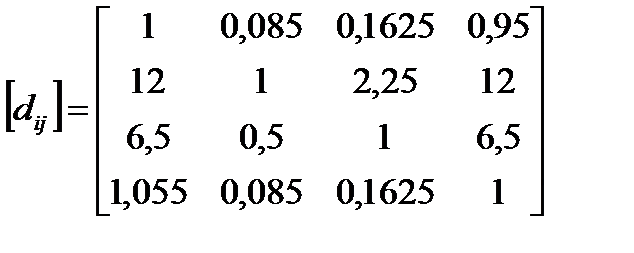 . Выбираем . Выбираем 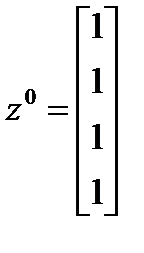 . .
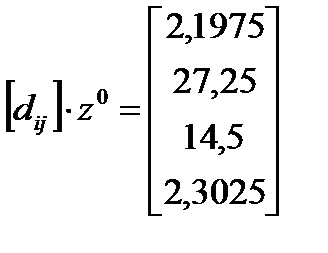 . . 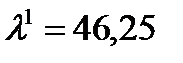 и и 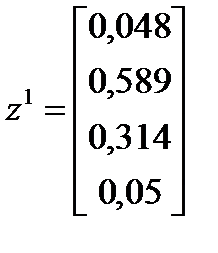 . Далее повторяем итерации. . Далее повторяем итерации.
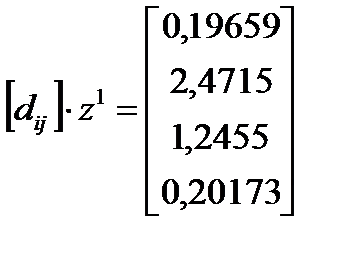 . . 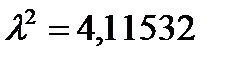 и и 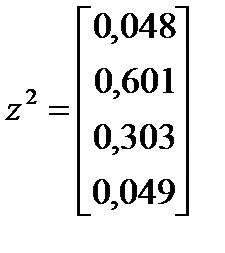 . . 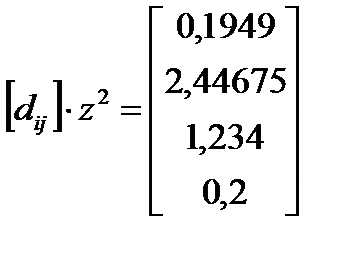 . . 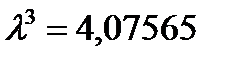 и и 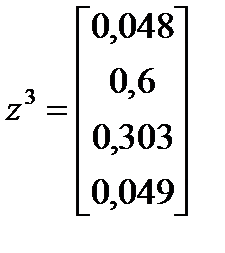 .
Изменения прекратились и вычисления можно закончить. .
Изменения прекратились и вычисления можно закончить.
|
Рекомендуемая литература.
1. Теория статистики. Учебник. Под ред. Громыко Г.Л. М. Инфра-М, 2010.
2. Едронова В.Н., Малафеева М.В. Общая теория статистики. Учебник. М. Магистр, 2010.
3. Шмойлова Р.А. , В.Г. Минашкин Теория статистики: учебно-методический комплекс-М: Издательский центр ЕАОИ, 2008.
4. Эндрю Ф. Сигел. Практическая бизнес–статистика. Вильямс, 2008.
Дата добавления: 2016-02-27; просмотров: 872;

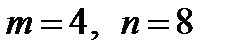 ). Результаты приведены в таблице.
). Результаты приведены в таблице.
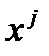
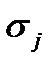
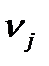
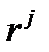
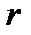
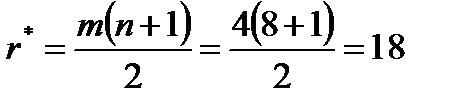 ;
;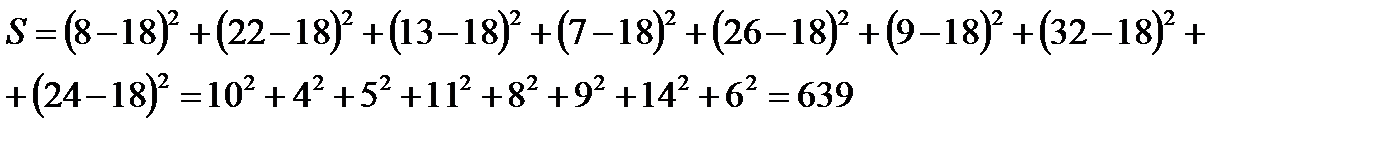
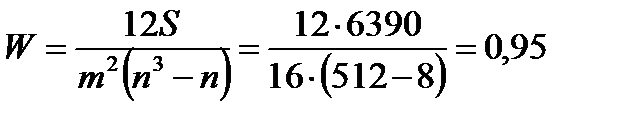 ;
;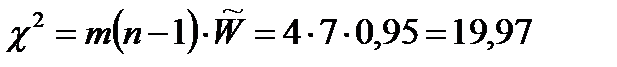 ;
;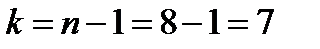 .
.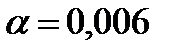 .
.