Теоретические основы. Давление в покоящейся жидкости
Давление в покоящейся жидкости
Распределение давления в покоящейся жидкости находится из уравнений равновесия Эйлера:
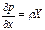
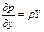или dp = ρ (Xdx + Ydy + Zdz), (2.1.1)
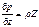
в которых, вектор 
, с компонентами (X, Y, Z) называется плотностью массовых сил или напряжением массовых сил (массовая сила, рассчитанная на единицу массы; размерность — ускорение). Дифференциальное уравнение поверхности равного давления (изобарической поверхности), имеет вид:
Xdx + Ydy + Zdz=0 (2.1.2)
Поверхность раздела между жидкой и газообразной средой называется свободной поверхностью.
В однородной несжимаемой жидкости (ρ = const), находящейся в равновесии под действием силы тяжести (X = 0, Y = 0, Z = - g, ось z направлена вверх), распределение давления определяется из выражения
p = p0 + ρg(z0 - z) = p0 + ρgh , (2.1.3)
где р0 — давление в точках горизонтальной плоскости с координатой z0 (в качестве такой плоскости чаще всего выбирается свободная поверхность жидкости); z — координата точки, в которой определяется давление р; h = z0 -z — глубина погружения рассматриваемой точки по отношению к плоскости с координатой z0; g — ускорение свободного падения (рис. 2.1.1).
Формула (2.1.3) носит название основного уравнения гидростатики. Из нее следует закон Паскаля: изменение давления в какой-либо покоящейся и продолжающей оставаться в покое точке жидкости передается одинаковым образом всем точкам этой жидкости. В совершенном газе, т.е. газе, подчиняющемся закону Клапейрона, находящемся в равновесии под действием силы тяжести, распределение давления при условии постоянства температуры по высоте (T=const) определяется барометрической формулой
(2.1.4)
где ро, ρо — соответственно абсолютное давление и плотность газа в точках горизонтальной плоскости с координатой z0.
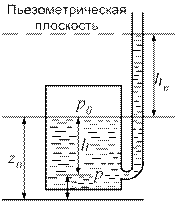
Рис. 2.1.1. Закрытый сосуд с покоящейся жидкостью (справа показана вертикальная открытая трубка - пьезометр)
Из формулы (2.1.4) можно найти высоту:
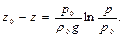(2.1.5)
Эта формула называется формулой барометрического нивелирования, так как позволяет определять разность высот по показаниям двух барометров.
Из формул (2.1.3) и (2.1.4) следует, что поверхностями равного давления для жидкости и газа, находящихся в абсолютном покое, являются горизонтальные плоскости:
z = const.
Простейшим прибором для измерения давления в сосуде с жидкостью является пьезометр, представляющий собой вертикальную открытую сверху стеклянную трубку, присоединяемую к сосуду (см. рис. 2.1.1). Пьезометр измеряет избыточное давление на поверхности жидкости в сосуде; пьезометрическая высота равна:
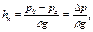(2.1.6)
где pа — атмосферное давление.
Назовем пьезометрической поверхностью поверхность, проходящую через уровень жидкости в пьезометре, или, ту же, поверхность, на которой давление равно атмосферному.
Если р0 > pа , то Δр > 0, и пьезометрическая поверхность располагается выше уровня жидкости в сосуде; если р0 < ра, тоΔр<0, и она находится ниже уровня жидкости; если р0 = ра , то пьезометрическая поверхность совпадает с поверхностью жидкости.
Для измерения давления применяются следующие приборы: барометры измеряют атмосферное давление, манометры — избыточное (на рис. 2.1.5 показан жидкостный манометр), вакуумметры – вакуум; для измерения разности давления в двух точках применяются дифференциальные манометры (см. рис. 2.1.7).
Вопросы для самопроверки
1. Какие виды давления вы знаете, и какими приборами они измеряются?
2. Каково численное соотношение между единицами давления "Паскаль" и "техническая атмосфера"?
3. Как запишется основное уравнение гидростатики, если известно ри на свободной поверхности жидкости, и требуется определить абсолютное давление в ниже расположенной точке?
4. Какой вид давления обязательно используется в формулах барометрической и барометрического нивелирования?
5. Где расположена пьезометрическая поверхность для открытого сосуда с жидкостью?
Дата добавления: 2016-02-27; просмотров: 2228;