Примеры решения задач на давление в жидкостях.

Пример 1. В закрытом резервуаре с нефтью плотностью ρ = 880 кг/м³ вакуумметр, установленный на его крышке, показывает р_в = 1,18 ? 10⁴ Па (рис. 2.1.2).

Определить показание манометра р_м, присоединенного к резервуа­ру на глубине Н = 6 м от поверхности жидкости, и положение пьезомет­рической плоскости.

Решение: Проведем плоскость 1 - 1 на уровне присоединения манометра. В этой плоскости абсолютное давление в соответствии с ос­новным уравнением гидростатики (2.1.3) равно:

р_1-1 = р₀ + ρgH,

где р₀ — абсолютное давление на поверхности, равное р_а — р_в.

Тогда

р_1-1 = р_а — р_в + ρgH.

С другой стороны, так как манометр измеряет избыточное давление (р_м=р_и), то

р_1-1 = р_а + р_м .

Приравняв два выражения для р_1-1, найдем р_м:

р_м = - р_в + ρgH = - 1,18?10⁴ + 880?9,8?6 = 3,99?10⁴ Па.

Так как на поверхности жидкости давление меньше атмосферного, то пьезометрическая высота отрицательна:

м,

и пьезометрическая плоскость расположена ниже поверхности жидкости на расстоянии 1,37 м.

Пример 2. Найти избыточное давление в сосуде А с водой по пока­заниям многоступенчатого двухжидкостного ртутного манометра (рис. 2.1.3): h₁ = 82 см; h₂ = 39 см; h₃ = 54 см; h₄ = 41 см; h₅ = 100 см; ρ_в=10³кг/м³; ρ_р=1,36?10⁴ кг/м³.

Решение: Так как жидкость находится в равновесии, то давления в точке 1 и в точке 2 равны как давления в точках одного и того же объе­ма однородной покоящейся жидкости, расположенных на одной горизон­тали, т.е. р₁ = р₂. На том же основании р₃ = р₄, р₅ = р₆ . В то же время избыточное давление

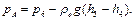
Исключив из этих соотношений промежуточные давления p₂, p₄, p₆, получим:

р_А = ρ_рg[(h₁ – h₂) + (h₃ – h₄ )] — ρ_вg[(h₃ - h₂ ) + (h₅ - h₄)] = =1,36?10⁴?9,8 (0,43+0,13) - 10³?9,8 (0,15 + 0,59) = 67,4 кПа.

Пример 3. Определить давление на забое закрытой газовой скважины (рис. 2.1.4.), если глубина скважины Н = 2200 м, манометрическое давление на устье р_м = 10,7 МПа, плотность природного газа при атмосферном давлении и температуре в скважине (считаемой неизменной по высоте) ρ = 0,76 кг/м3, атмосферное давление р_а = 98 кПа.

Решение:

Для определения давления на забое газовой скважины воспользуемся барометрической формулой 

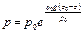
В нашей задаче р₀ – абсолютное давление газа на устье скважины

р₀ = р_а + р_м = 9,8 ? 10³ + 10,7 ? 10⁶ =

= 10,8 ? 10⁶ Па;

ρ₀ – плотность при давлении р₀, а z₀ – z = 2200 м.

Из уравнения состояния газа следует, что

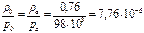с²/м²,

а показатель степени:

Тогда

р = 10,8 ? 10⁶ ? е ^0,167 = 12,8 МПа.