Теоретические основы. Из теоретической механики известно, что в общем случае система сил давления, приложенных к криволинейной поверхности

Из теоретической механики известно, что в общем случае система сил давления, приложенных к криволинейной поверхности, приводится к главному вектору и главному моменту сил давления. В частных слу­чаях (сфера, цилиндр с вертикальной или горизонтальной осью) силы давления приводятся только к равнодействующей (главному вектору).

Равнодействующая сил давления Р определяется из выражения

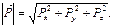(2.1.12)

Положение в пространстве вектора силы Р задано направляющими косинусами:

cos(Р, х) = 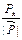, cos(Р, у) = 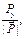cos(P, z) = 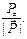(2.1.13)

Примем, что ось z направлена вертикально вверх:

Горизонтальная составляющая Р_г (Р_х или Р_у ) определяется по формуле

Р_г = (р_т – р_а) s_в (2.1.14)

где s_в — площадь проекции рассматриваемой криволинейной поверх­ности на вертикальную плоскость, нормальную к соответствующей оси координат (yoz для силы Р_х, xoz для силы Р_у); р_т — абсолютное дав­ление в центре тяжести площади s_в; р_а — атмосферное давление.

Формула (2.1.14) аналогична формуле (2.1.7), используемой для слу­чая определения силы давления на плоские поверхности, где роль послед­ней исполняет вертикальная проекция криволинейной поверхности.

Направление действия силы Р_г зависит от знака величины р_т – р_а (при р_т - р_а > 0 — наружу, при р_т - р_а < 0 — вовнутрь жидкости), при­чем линия ее действия проходит через центр давления площади s_в.

Вертикальная составляющая силы Р определяется весом тела давления

Р_z = ρgV_т.д, (2.1.15)

где V_т.д — объем тела давления.

Телом давления называется объем, ограниченный рассматривае­мой криволинейной поверхностью, ее проекцией на пьезометрическую поверхность и боковой цилиндрической поверхностью, образующейся при проектировании (рис. 2.1.21).

Рис. 2.1.21. Схема сосуда с жидкостью, ограниченного криволинейными поверхностями (показаны элементарные составляющие сил давления жидкости на стенки сосуда)

Для криволинейной поверхности ABC (см. рис. 2.1.21) телом давле­ния будет фигура ABCEFA, для криволинейной поверхности ADC - ADCEFA.

Направление действия вертикальной составляющей Р_z зависит от направления элементарных составляющих этой силы.

На примере рис. 2.1.21 видно, что давление в любой точке криволиней­ных поверхностей — как ABC, так и ADC — избыточное (пьезометричес­кая плоскость лежит выше этих поверхностей). Следовательно, элемен­тарные

силы давления dP, действующие по нормали к касательной в лю­бой точке этих поверхностей, направлены наружу.

Разложение их на составляющие показывает, что вертикальная составляющая силы Р действует на поверхность ABC вверх, а на поверх­ность ADC вниз (их результирующая сила направлена вниз и равна весу реальной жидкости в объеме ABCD, являющемся результирующим объемом двух тел давления).

Линия действия вертикальной составляющей силы Р проходит через центр тяжести рассматриваемого тела давления.

Закон Архимеда: на тело, погруженное в жидкость, действует выталкивающая сила Р_А, равная по величине весу жидкости в объеме погруженной части тела V:

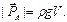(2.1.16)

Выталкивающая (Архимедова) сила приложена в центре тяжести объема погруженной части тела, называемом центром водоизмещения.

Плавающее тело обладает остойчивостью (способностью возвра­щаться в состояние равновесия после получения крена) в случае, если точка пересечения линии действия выталкивающей силы с осью плава­ния (метацентр) лежит выше центра тяжести тела.

Вопросы для самопроверки

1. В чем сходство и различие формул для определения горизонталь­ной составляющей силы давления жидкости на криволинейную поверх­ность и силы давления на плоскую поверхность?

2. Что называется "телом давления"?

3. Если в нижней точке криволинейной поверхности в жидкости, находящийся над ней, вакуум, то как по отношению к этой поверхности
располагается "тело давления" и каково направление вертикальной
составляющей силы давления?

4. Если тело тонет, то куда направлена Архимедова сила?