Теоретические основы. Скорость частицы жидкости зависит от координат x, y, z этой частицы и времени t, т.е.

Скорость частицы жидкости 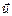зависит от координат x, y, z этой частицы и времени t, т.е.

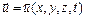
Плотность ρ и давление p также являются функциями координат и времени:

ρ = ρ (х, y, z, t); р = р(х, у, z, t).

Если характеристики течения не зависят от времени, т.е. могут изменяться лишь от точки к точке, то течение называется установившимся. Если в данной точке пространства характеристики течения изменяются со временем, то течение называется неустановившимся.

Линией тока называется линия, в каждой точке которой вектор скорости 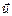направлен по касательной к этой линии. Уравнения для линий тока имеют вид

(2.2.1)

где - составляющие вектора скорости .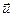

Совокупность линий тока, проходящих через замкнутый контур L, образует трубчатую поверхность - трубку тока. Жидкость, находящаяся внутри трубки тока образует струйку. Если контур L мал, то трубка тока и струйка называются элементарными.

Сечение струйки s, нормальное в каждой своей точке к линиям тока, называется живым сечением.

Область пространства конечных размеров, занятая движущейся жидкостью, называется потоком. Поток обычно рассматривается как совокупность элементарных струек. Живое сечение потока определяется так же, как в случае элементарной струйки.

Гидравлический радиус R_Г живого сечения определяется как отношение площади живого сечения s к смоченному периметру χ, т.е.

. (2.2.2)

Под смоченным периметром χ понимается та часть геометрического живого сечения, по которой жидкость соприкасается с твердыми стенками.

Если форма и площадь живого сечения по длине потока не изменяются, то поток называется равномерным. В противном случае поток называется неравномерным. В том случае, когда живое сечение плавно изменяется по длине, течение называется плавноизменяющимся.

В живом сечении 1—1 (рис. 2.2.1) равномерного потока выполняется гидростатический закон распределения давления, т.е.

(2.2.3)

где р_А, р_В - соответственно давления в произвольных точках А и В (с вертикальными координатами z_А, z_В) этого сечения; g - ускорение свободного падения. В случае плавноизменяющегося течения равенство 2.2.3 выполняется приближенно.

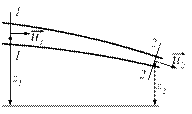
Рис. 2.2.1. Живое сечение равномерного потока

Рис. 2.2.2. Элементарная струйка

Расходом жидкости через поверхность s называется количество жидкости, протекающей через эту поверхность в единицу времени. Объемный расход Q, массовый расход Q_M, весовой расход Q_G определяются по формулам

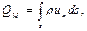
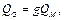(2.2.4)

где u_n - проекция скорости 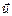на нормаль 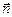к поверхности s.

Если s - живое сечение, то u_n = и. Для однородной жидкости

(2.2.5)

Средняя скоростьυ определяется из равенства

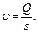(2.2.6)

Уравнение неразрывности для потока несжимаемой жидкости имеет вид

(1.2.7)

где υ₁, υ₂ - средние скорости в сечениях 1-1 и 2-2.

Уравнение Бернулли для элементарной струйки вязкой несжимаемой жидкости при установившемся движении в поле силы тяжести имеет вид

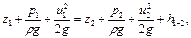(2.2.8)

где z₁, z₂ — расстояния от центров выбранных живых сечений 1 - 1 и 2 - 2 до некоторой произвольной горизонтальной плоскости z=0 (рис. 2.2.2); υ₁, υ₂ — скорости; p₁, p₂ — давления в этих сечениях; h_1-2 — потери напора на участке между выбранными сечениями.

Уравнение Бернулли выражает собой закон сохранения механической энергии. Величина

(2.2.9)

называется полным напором и представляет собой удельную (приходящуюся на единицу силы тяжести) механическую энергию жидкости в рассматриваемом сечении; z — геометрический напор или удельная потенциальная энергия положения; p/(ρg) - пьезометрический напор или удельная потенциальная энергия давления; u²/(2g) — скоростной напор или удельная кинетическая энергия; h_1-2 — потери напора, т.е. часть удельной механической энергии, израсходованной на работу сил трения на участке между сечениями 1-1 и 2-2 (см. рис. 2.2.2).

В случае идеальной жидкости h_1-2 = 0.

Для плавноизменяющегося потока при установившемся движении вязкой несжимаемой жидкости в поле силы тяжести уравнение Бернулли имеет вид

(2.2.10)

где p₁, p₂ - давления в произвольно взятых точках сечений 1 - 1 и 2 -2 с координатами z₁ и z₂ соответственно (обычно берутся точки на оси потока); υ₁, υ₂ - средние скорости в этих сечениях; α₁, α₂ — коэффициенты Кориолиса, учитывающие неравномерность распределения скоростей частиц жидкости в сечениях; при течении по круглой цилиндрической трубке α=2 для ламинарного режима течения и α≈1,1 — для турбулентного; при решении практических задач обычно принимается α=1.

При использовании уравнения Бернулли (2.2.8) или (2.2.10) необходимо иметь в виду, что номера сечений возрастают в направлении течения жидкости. В качестве расчетных выбираются такие сечения (струйки), в которых известны какие-либо из величины υ₁, υ₂ (и₁, и₂) и р₁, р₂.

Плоскость z = 0 бывает удобно располагать таким образом, чтобы центр одного из выбранных сечений потока лежал в этой плоскости.

Потери напора h_1-2, отнесенные к единице длины трубопровода, называются гидравлическим уклоном:

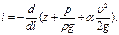(2.2.11)

<7 8 91011 12 13 >

Дата добавления: 2016-02-27; просмотров: 1418;