Примеры решения задач. Пример 2.2.1. Определить, пренебрегая потерями напора, скорость течения нефти на расстоянии r от оси трубопровода радиусом R при по­мощи устройства (трубка

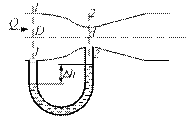
Пример 2.2.1. Определить, пренебрегая потерями напора, скорость течения нефти на расстоянии r от оси трубопровода радиусом R при по­мощи устройства (трубка Пито), показанного на рис. 2.2.3. Уровень жидкости в трубке А h₁ = 1,2 м, в трубке В h₂ = 1,35 м.

Рис. 2.2.3. Трубка Пито Рис. 2.2.4. Расходомер Вентури

Решение

Учитывая, что h_1-2 = 0 по условию, из уравнения Бернулли (2.2.8) для струйки, проходящей на расстоянии r от оси трубы имеем:

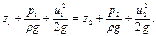
Так как трубопровод расположен горизонтально, то z₁ = z₂.Скорость в сечении 2 — 2 u₂ = 0, поскольку жидкость в трубке B нахо­дится в состоянии покоя. Тогда

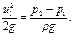
С учетом того, что давление в трубках и живых сечениях потока распределено по гидростатическому закону, получим:

С учетом того, что давление в трубках и живых сечениях потока распределено по гидростатическому закону, получим:

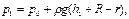
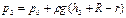
и

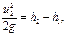
откуда

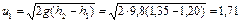м/с.

Пример 2.2.2. Найти при помощи устройства, показанного на рис. 2.2.4 (расходомер Вентури), объемный расход керосина (ρ = 850 кг/м³). Диаметр трубопровода D = 0,3 м; диаметр узкого сечения расходоме­ра d = 0,1 м. Разность уровней ртути в дифманометре Δh = 0,025 м. Режим течения турбулентный. Потерями напора можно пренебречь.

Решение

Проведем живые сечения 1 - 1 и 2 – 2 и запишем для них уравнение неразрывности (2.2.7) и уравнение Бернулли (2.2.10):

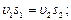
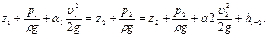
Так как труба горизонтальная, а потерями можно пренебречь, то z₁=z₂, h_1-2=0. Приняв, кроме того α₁=α₂=1 и исключив из этих уравнений υ₂, получим:

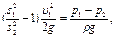
откуда

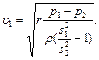
Разность давлений, измеренная дифманометром:

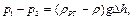
где ρ_РТ - плотность ртути.

Следовательно

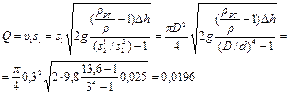
Пример 2.2.3. Определить полезную мощность насоса (рис. 2.2.5), перекачивающего бензин (ρ = 750 кг/м³) из резервуара A в резервуар В, если h₁ = 1 м, h₃ = 5 м, расход бензина Q = 10^-3 м³/с, D = 0,1 м; d = 0,05. Потери во всасывающей линии равны 2 м, а в нагнетательной 5 м. Оба резервуара открытые.

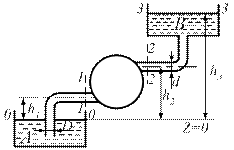
Рис. 2.2.5. Схема насосной установки

Решение

Разность полных удельных энергий в сечениях непо­средственно за насосом (2 - 2) и передним (1 - 1) представляет собой удельную энергию Н_Н, сообщенную насосом жидкости, т.е.

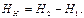
Тогда полезная мощность насоса :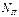

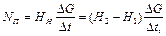
где ΔG - вес перекачанной жидкости за время Δt .

Поскольку очевидно, что

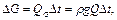
то

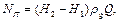(2.2.13)

где Н₁-Н₂ - напор создаваемый насосом Н_нас.

Для определения полных напоров Н₁ и Н₂ рассмотрим участки трубопровода между сечениями 0 - 0 и 1 - 1 (всасывающая линия), а также 2 – 2 и 3 - 3 (нагнетательная линия). Записав для каждого из этих участков

уравнение Бернулли, имеем соответственно:

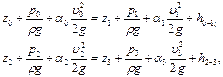
где z₀ = 0, z₁ = h₁, z₃ = h₃ .

Так как резервуары открыты, то p₀ = p₃ = p_a. Площади свободных поверхностей резервуаров A и B велики по сравнению с площадями живых сечений труб. Поэтому можно принять υ₀=υ₃=0.

Тогда

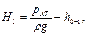
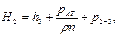
Вт.