Проверка гипотезы о значимости выборочного коэффициента корреляции

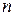Пусть двумерная генеральная совокупность , распределена нормально. Из этой совокупности извлечена выборка объема и по ней найден выборочный коэффициент корреляции , который оказался отличным от 0.

Так как выборка отобрана случайно, то еще нельзя заключить, что коэффициент корреляции генеральной совокупности 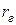также отличен от 0.

Нас интересует именно этот коэффициент 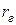. Поэтому возникает необходимость при заданном уровне значимости a проверить нулевую гипотезу 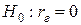о равенстве нулю генерального коэффициента корреляции при конкурирующей гипотезе .

Если гипотеза будет опровергнута, то это означает, что выборочный коэффициент корреляции значительно отличается от 0, а и связаны линейной зависимостью.

Если нулевая гипотеза будет принята, то выборочный коэффициент корреляции не значим, а и не связаны линейной зависимостью.

В качестве критерия проверки нулевой гипотезы примем случайную величину 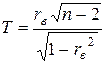, где 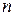– объем выборки.

Величина при справедливости нулевой гипотезы имеет распределение Стьюдента с 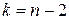степенями свободы. Обозначим значение критерия, вычисленное по данным наблюдений через и сформулируем правило проверки нулевой гипотезы.

Для того чтобы при заданном уровне значимости 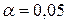проверить нулевую гипотезу 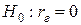о равенстве нулю генерального коэффициента корреляции нормальной двумерной случайной величины, при конкурирующей гипотезе надо вычислить наблюдаемое значение критерия 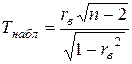и по таблице критических точек распределения Стьюдента по заданному уровню значимости 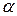и числу степеней свободы 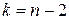найти критическую точку для двусторонней критической области.

Если – нет основания отвергнуть нулевую гипотезу. Если – нулевую гипотезу отвергают и, следовательно, выборочный коэффициент корреляции значимо отличается от 0 , то есть и линейно корреляционны.