Задачи регрессионного анализа

Основные задачи теории корреляции

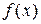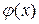1. Установить форму корреляционной связи, то есть вид функции регрессии (линейная, квадратичная, показательная и т. д.). Наиболее часто функции регрессии оказываются линейными. Если обе функции регрессии и линейны, то корреляцию называют линейной, в противном случае ее называют нелинейной.

2. Оценить тесноту корреляционной связи. Теснота корреляционной зависимости оценивается по величине рассеивания значения вокруг условной средней .Большое рассеивание свидетельствует о слабой зависимости от , либо об отсутствии зависимости. Малое рассеивание указывает на наличие достаточно сильной зависимости, возможно даже, что и связаны функционально, но под воздействием случайных факторов эта связь оказалась размытой, в результате чего при одном и том же значении величина принимает различные значения.

Задачи регрессионного анализа

Регрессионный анализ – анализ функции регрессии. С его помощью решаются следующие задачи:

1. Находят точечные и интервальные оценки параметров элементарной функции регрессии.

2. Производят точечные и интервальные оценки, необходимые для предсказания средних значений одной случайной величины, соответствующие функциональной зависимости от другой величины.

3. Производят согласование найденной элементарной функции с экспериментальными данными.

Корреляционная таблица

При большом количестве наблюдений одного и того же значения, значение 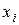может встретиться 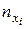раз, одно и то же значение 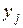– 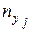раз. Одна и та же пара чисел может встретиться раз. Поэтому данные наблюдений группируются, то есть подсчитываются частоты , , .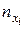

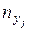Все сгруппированные данные записываются в виде таблицы, которую называют корреляционной. Интервалы одной случайной величины записывают в первый столбец корреляционной таблицы, а интервалы другой случайной величины – в первую строку.

По каждой паре значений решают в какую строку и в какой столбец они попадают. В клетку, стоящую на пересечении соответствующих строки и столбца, ставят точку. Так поступают со всеми парами чисел . Затем подсчитывают точки во всех клетках и записывают соответствующим числом .

Далее суммируют числа 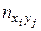по строкам и столбцам и находим 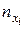и .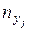

Замечание. .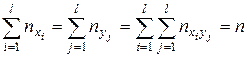

Для каждого столбца необходимо найти условное среднее 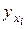, а для каждой строки .