Преобразования Лапласа.
Исследование АСР существенно упрощается при использовании прикладных математических методов операционного исчисления. Например, функционирование некоторой системы описывается ДУ вида
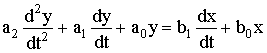 , (2.1)
, (2.1)
где х и у - входная и выходная величины. Если в данное уравнение вместо x(t) и y(t) подставить функции X(s) и Y(s) комплексного переменного s такие, что
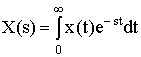 и
и 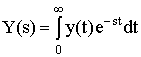 , (2.2)
, (2.2)
то исходное ДУ при нулевых начальных условиях равносильно линейному алгебраическому уравнению
a2 s2 Y(s) + a1 s Y(s) + a0 Y(s) = b1 X(s) + b0 X(s).
Такой переход от ДУ к алгебраическому уравнению называется преобразованием Лапласа, формулы (2.2) соответственно формулами преобразования Лапласа, а полученное уравнение - операторным уравнением.
Новые функции X(s) и Y(s) называются изображениями x(t) и y(t) по Лапласу, тогда как x(t) и y(t) являются оригиналами по отношению к X(s) и Y(s).
Переход от одной модели к другой достаточно прост и заключается в замене знаков дифференциалов 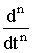 на операторы sn, знаков интегралов
на операторы sn, знаков интегралов  на множители
на множители 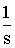 , а самих x(t) и y(t) - изображениями X(s) и Y(s).
, а самих x(t) и y(t) - изображениями X(s) и Y(s).
Для обратного перехода от операторного уравнения к функциям от времени используется метод обратного преобразования Лапласа. Общая формула обратного преобразования Лапласа:
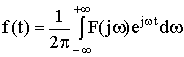 , (2.3)
, (2.3)
где f(t) - оригинал, F(jw) - изображение при s = jw, j - мнимая единица, w - частота.
Эта формула достаточно сложна, поэтому были разработаны специальные таблицы, в которые сведены наиболее часто встречающиеся функции F(s) и их оригиналы f(t). Они позволяют отказаться от прямого использования формулы (2.3).
Таблица преобразований Лапласа
| Оригинал x(t) | Изображение X(s) |
| d-функция | |
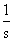
| |
| t | 
|
| t2 | 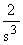
|
| tn | 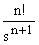
|
| e-at | 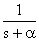
|
| a.x(t) | a.X(s) |
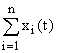
| 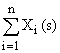
|
| x(t - a) | X(s).e-as |
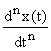
| sn.X(s) |
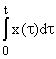
| 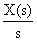
|
Дата добавления: 2016-02-24; просмотров: 570;
