Примеры типовых звеньев.

Звеном системы называется ее элемент, обладающий определенными свойствами в динамическом отношении. Звенья систем регулирования могут иметь разную физическую основу (электрические, пневматические, механические и др. звенья), но относится к одной группе. Соотношение входных и выходных сигналов в звеньях одной группы описываются одинаковыми передаточными функциями.

Простейшие типовые звенья:

· усилительное,

· интегрирующее,

· дифференцирующее,

· апериодическое,

· колебательное,

· запаздывающее.

1) Усилительное звено.

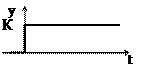Звено усиливает входной сигнал в К раз. Уравнение звена у = К*х, передаточная функция W(s) = К. Параметр К называется коэффициентом усиления.

Выходной сигнал такого звена в точности повторяет входной сигнал, усиленный в К раз.

Примерами таких звеньев являются: механические передачи, датчики, безынерционные усилители и др.

2) Интегрирующее.

2.1) Идеальное интегрирующее.

Выходная величина идеального интегрирующего звена пропорциональна интегралу входной величины.

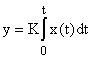; W(s) =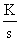

При подаче на вход звена воздействия выходной сигнал постоянно возрастает.

Это звено астатическое, т.е. не имеет установившегося режима.

2.2) Реальное интегрирующее.

Передаточная функция этого звена имеет вид: W(s) = .

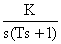Переходная характеристика в отличие от идеального звена является кривой.

Примером интегрирующего звена является двигатель постоянного тока с независимым возбуждением, если в качестве входного воздействия принять напряжение питания статора, а выходного - угол поворота ротора.

3) Дифференцирующее.

3.1) Идеальное дифференцирующее.

Выходная величина пропорциональна производной по времени от входной:

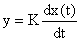; W(s) = K*s

При ступенчатом входном сигнале выходной сигнал представляет собой импульс (d-функцию).

3.2) Реальное дифференцирующее.

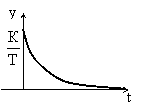Идеальные дифференцирующие звенья физически не реализуемы. Большинство объектов, которые представляют собой дифференцирующие звенья, относятся к реальным дифференцирующим звеньям. Переходная характеристика и передаточная функция этого звена имеют вид:

W(s) = .

4) Апериодическое (инерционное).

Этому звену соответствует ДУ вида:

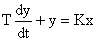; W(s) = .

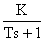Определим характер изменения выходной величины этого звена при подаче на вход ступенчатого воздействия величины х₀.

Изображение ступенчатого воздействия: X(s) = 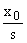. Тогда изображение выходной величины:

Y(s) = W(s) X(s) = 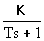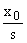= K x₀ .

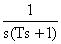Разложим дробь на простые:

= + = = - = -

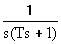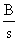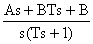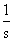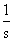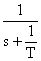
Оригинал первой дроби по таблице: L^-1{ 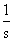} = 1, второй: L^-1{ } = .

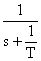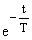Тогда окончательно получаем:

y(t) = K x₀ (1 - ).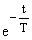

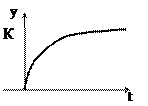Постоянная Т называется постоянной времени.

Большинство тепловых объектов являются апериодическими звеньями. Например, при подаче на вход электрической печи напряжения ее температура будет изменяться по аналогичному закону.

5) Колебательное звено имеет ДУ вида

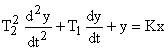или W(s) = .

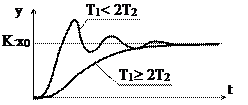При подаче на вход ступенчатого воздействия амплитудой х₀ на переходная кривая будет

иметь один из двух видов: апериодический (при Т₁ ³ 2Т₂) или колебательный (при Т₁ < 2Т₂).

6) Запаздывающее.

y(t) = x(t - t), W(s) = e^-ts.

Выходная величина у в точности повторяет входную величину х с некоторым запаздыванием t. Пример: конвейер.