Определение частотных характеристик.

Известно, что динамические процессы могут быть представлены частотными характеристиками (ЧХ) путем разложения функции в ряд Фурье.

Предположим, имеется некоторый объект и требуется определить его ЧХ. При экспериментальном снятии ЧХ на вход объекта подается синусоидальный сигнал с амплитудой А_вх = 1 и некоторой частотой w, т.е. x(t) = А_вхsin(wt) = sin(wt).

Тогда после прохождения переходных процессов на выходе мы будем также иметь синусоидальный сигналтой же частоты w, но другой амплитуды А_вых и фазы j: у(t) = А_выхsin(wt + j)

При разных значениях w величины А_вых и j, как правило, также будут различными. Эта зависимость амплитуды и фазы от частоты называется частотной характеристикой. Виды ЧХ:

· АФХ - зависимость амплитуды и фазы от частоты (изображается на комплексной плоскости);

· АЧХ - зависимость амплитуды от частоты;

· ФЧХ - зависимость фазы от частоты;

· ЛАХ, ЛАЧХ - логарифмические АЧХ.

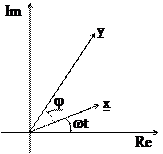На комплексной плоскости входная величина x = А_вх^.sin(wt) для каждого момента времени t_i определяется вектором х на комплексной плоскости. Этот вектор имеет длину, равную А_вх, и отложен под углом wt_i к действительной оси. (Re - действительная ось, Im - мнимая ось)

Тогда величину х можно записать в комплексной форме

х(t) = А_вх(cos(wt) + j^.sin(wt)),

где j = 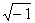- мнимая единица.

Или, если использовать формулу Эйлера

e^ja = cosa + j^.sina,

то можно записать х(t) = А_вх^.e^jwt.

Выходной сигнал y(t) можно аналогично представить как вектор y(t) = А_вых^.e^j(wt+j).

Рассмотрим связь передаточной функции и частотной характеристики.

Определим производные по Лапласу:

у ® Y

у’ ® sY

у” ® s²Y и т.д.

Определим производные ЧХ:

у’(t) = jw А_выхе^{j(wt + j)} = jw у,

у”(t) = (jw)² А_выхе^{j(wt + j)} = (jw)² у и т.д.

Отсюда видно соответствие s = jw. Вывод: частотные характеристики могут быть построены по передаточным функциям путем замены s = jw.

Пример: .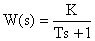

При s = jw имеем:

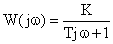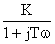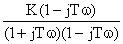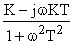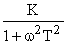= = = = - j =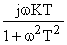

= Re(w) + j Im(w).

Изменяя w от 0 до ¥, можно построить АФХ (см. рис.).

Для построения АЧХ и ФЧХ используются формулы:

, .

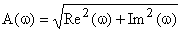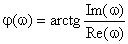Формулы получения АФХ по АЧХ и ФЧХ:

Re(w) = A(w) cos j(w), Im(w) = A(w) sin j(w).