Поверхность произвольных размеров и формы
Произвольную поверхность  разбиваем системой взаимно перпендикулярных и равноотстоящих плоскостей на совокупность бесконечно малых кубических объемов. (Путем бесконечного уменьшения расстояния между плоскостями можно бесконечно приблизиться к кубическим объемам, заполняющим поверхность произвольной формы).
разбиваем системой взаимно перпендикулярных и равноотстоящих плоскостей на совокупность бесконечно малых кубических объемов. (Путем бесконечного уменьшения расстояния между плоскостями можно бесконечно приблизиться к кубическим объемам, заполняющим поверхность произвольной формы).
Складывая потоки по всем кубикам, имеем:
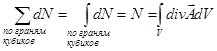 .
.
Теперь грани кубиков разделим на 2 класса.
I класс: грани внешние, совпадающие с элементами поверхности 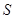 .
.
II класс: грани внутренние, отделяющие кубики друг от друга.
В сумму 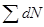 поток через каждую внутреннюю грань войдет дважды: один раз со знаком «+», второй раз со знаком «-» (направление внешней нормали для одной поверхности будет совпадать с положительным направлением соответствующей оси координат, а для другой поверхности – с отрицательным направлением). Следовательно, все слагаемые суммы
поток через каждую внутреннюю грань войдет дважды: один раз со знаком «+», второй раз со знаком «-» (направление внешней нормали для одной поверхности будет совпадать с положительным направлением соответствующей оси координат, а для другой поверхности – с отрицательным направлением). Следовательно, все слагаемые суммы 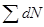 , относящиеся к внутренним граням, взаимно уничтожаются, поток определится суммой
, относящиеся к внутренним граням, взаимно уничтожаются, поток определится суммой 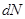 только по граням I класса, совпадающим с поверхностью
только по граням I класса, совпадающим с поверхностью 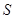 . Отсюда:
. Отсюда:
 .
.
Теорема Гаусса из векторного анализа
Поток вектора 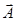 , являющегося непрерывной функцией точки, через произвольную замкнутую поверхность
, являющегося непрерывной функцией точки, через произвольную замкнутую поверхность 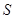 равен интегралу от дивергенции этого вектора по объему
равен интегралу от дивергенции этого вектора по объему 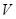 , ограниченному этой поверхностью.
, ограниченному этой поверхностью.
Обращаясь снова к электростатике, применим этот результат к электростатической теореме Гаусса:
 .
.
Это преобразование, однако, возможно лишь в том случае, если 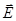 является непрерывной функцией точки (т.е.
является непрерывной функцией точки (т.е. 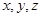 ), т.е. имеет конечное значение во всех точках объема
), т.е. имеет конечное значение во всех точках объема  , ограниченного поверхностью
, ограниченного поверхностью 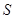 , т.е. если
, т.е. если 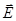 конечно и непрерывно во всех точках объема. Это означает, что внутри
конечно и непрерывно во всех точках объема. Это означает, что внутри  не должно быть ни точечных зарядов конечной величины (так как при
не должно быть ни точечных зарядов конечной величины (так как при 
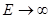 , а направление
, а направление 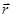 становится неопределенным), ни поверхностных зарядов конечной поверхностной плотности (так как на заряженных поверхностях
становится неопределенным), ни поверхностных зарядов конечной поверхностной плотности (так как на заряженных поверхностях 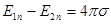 - разрыв нормальной составляющей
- разрыв нормальной составляющей 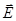 ).
).
На самом деле понятия точечного или поверхностного заряда следует рассматривать как понятия вспомогательные. Чтобы иметь возможность изучать электрическое поле вблизи или даже внутри заряженных объемов, следует ввести понятие об объемной плотности заряда: 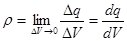 .
.
Вспомним задачу о поле равномерно заряженного по объему шара.
Nbsp; РИС.14-2
Этот конкретный пример имеет общее значение:
Если объемная плотность заряда 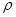 конечна, то вектор электрического поля всюду непрерывен и конечен.
конечна, то вектор электрического поля всюду непрерывен и конечен.
Следовательно, 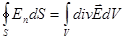 .
.
По определению объемной плотности заряда 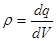 .
.
Полный заряд в объеме  :
:  .
.
Теперь электростатическая теорема Гаусса будет иметь вид:
 .
.
Поскольку равенство объемных интегралов должно иметь место независимо от конкретного объема  , должны быть равны подынтегральные выражения:
, должны быть равны подынтегральные выражения:
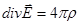 ,
,
или в декартовой системе координат:
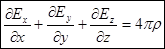 .
.
Фактически уже получено одно из уравнений Максвелла (уравнение (4) в нашей записи).
Для вакуума 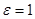 , следовательно,
, следовательно, 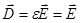 .
.
Заметим, что по-прежнему этого одного скалярного уравнения недостаточно, чтобы определить поле вектора 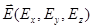 .
.
Работа сил электрического поля
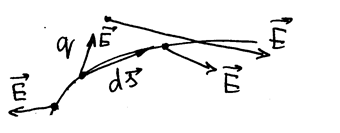 |
РИС.14-3
Точечный заряд 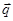 перемещается на отрезок
перемещается на отрезок  поле
поле 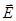 .
.
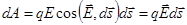 .
.
При перемещении единичного заряда по конечному пути 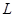 :
:
 .
.
Электрическое поле неподвижных зарядов (т.е. электростатическое поле) обладает важной особенностью: работа сил электростатического поля при перемещении [единичного] заряда между двумя точками зависит только от положения этих точек и не зависит от формы пути.
Вспомним общие положения.
1) Если силовое поле стационарно и силы, действующие на помещенное в это поле тело, зависят только от его положения, но не от его скорости, то работа сил этого поля не зависит от формы пути между положениями начальной и конечной точек.
2) Если работа сил некоторого силового поля на пути между двумя точками зависит только от положения этих точек и вовсе не зависит от формы пути между этими точками, то поле называется консервативным или потенциальным.
3) В потенциальном поле работа сил на всяком замкнутом пути равна нулю; следовательно, для электростатического поля:
 .
.
Этот линейный интеграл называется циркуляцией вектора 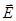 вдоль замкнутого контура
вдоль замкнутого контура 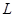 .
.
Математическое отступление
Пусть в поле вектора 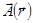 (дифференцируемого) задана некоторая кривая
(дифференцируемого) задана некоторая кривая 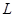 и указано, какое направление по этой кривой считается положительным.
и указано, какое направление по этой кривой считается положительным.
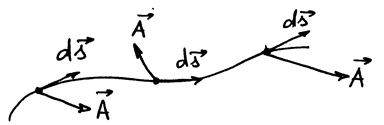 |
Разбиваем кривую
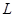 на бесконечно малые элементы
на бесконечно малые элементы 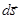 , направление которых совпадает с положительным направлением на кривой
, направление которых совпадает с положительным направлением на кривой 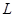 , умножаем каждый элемент скалярно на значение
, умножаем каждый элемент скалярно на значение 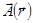 в соответствующей точке и суммируем полученные величины.
в соответствующей точке и суммируем полученные величины.
РИС.14-4

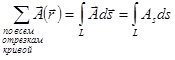 , так как
, так как 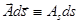 .
.
Если кривая 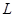 замкнута, то предел суммы произведений
замкнута, то предел суммы произведений 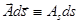 по всем отрезкам
по всем отрезкам  вдоль контура
вдоль контура 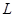 называется циркуляцией вектора
называется циркуляцией вектора 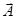 вдоль контура
вдоль контура 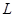 :
:

 .
.

Рассмотрим циркуляцию произвольного вектора 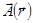 (дифференцируемого) по бесконечно малому контуру
(дифференцируемого) по бесконечно малому контуру 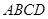 (прямоугольник).
(прямоугольник).
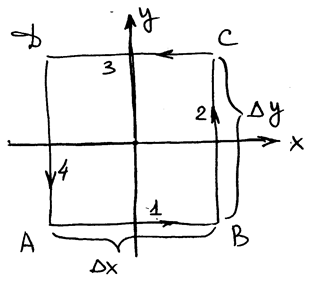 |
РИС.14-5
Ось 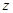 направлена на нас,
направлена на нас, 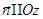 , положительным объявляем такое направление обхода контура, чтобы обход осуществлялся против часовой стрелки, если смотреть со стороны нормали
, положительным объявляем такое направление обхода контура, чтобы обход осуществлялся против часовой стрелки, если смотреть со стороны нормали 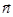 .
.
Делаем прямоугольник 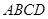 настолько малым, чтобы вектор
настолько малым, чтобы вектор 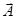 мало менялся на протяжении одной стороны.
мало менялся на протяжении одной стороны.
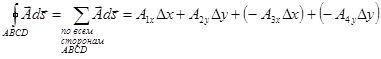 , где
, где
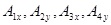 - соответствующие средние значения вектора
- соответствующие средние значения вектора 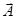 на каждой стороне.
на каждой стороне.
Рассмотрим слагаемые 1 и 3: 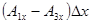 .
.
Устремляя длину сторон прямоугольника к нулю, т.е. 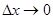 , находим величину
, находим величину
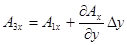 , где под
, где под 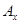 следует понимать значение в центре прямоугольника.
следует понимать значение в центре прямоугольника.
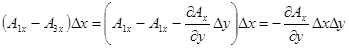 .
.
Слагаемые 2 и 4:
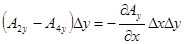 , так как
, так как 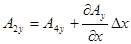 .
.
Итак,  .
.
При бесконечной малости прямоугольника
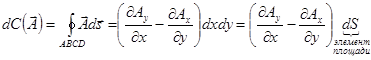 .
.
Рассмотрим теперь прямоугольную площадку, перпендикулярную оси 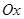 (
( 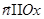 ):
):
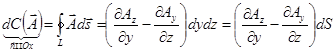 .
.
Для площадки, перпендикулярной 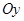 (
( 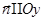 ):
):
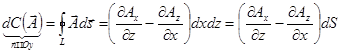 .
.
Будем рассматривать эти комбинации чисел как компоненты некоторого вектора, который назовем 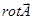 :
:
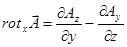 ,
, 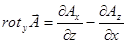 ,
, 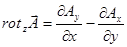 .
.
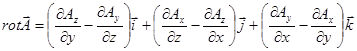 .
.
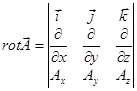 .
.
С использованием векторного оператора 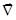 :
:
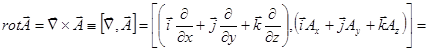
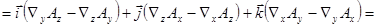
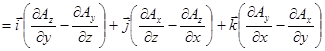 .
.
Полученные результаты можно записать в виде:
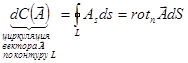
(индекс  означает положительную нормаль к площадке
означает положительную нормаль к площадке  ).
).
Определение:
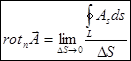 .
.
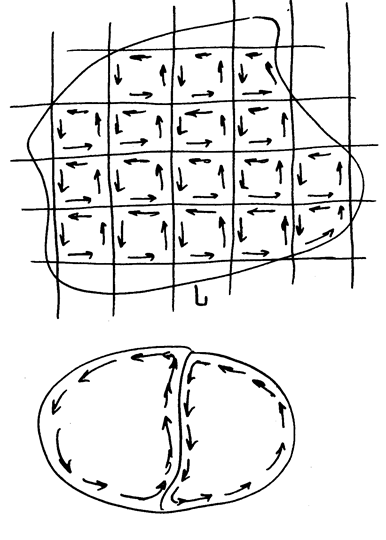 |
Рассмотрим теперь циркуляцию вектора
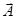 по контуру площадки произвольной формы и произвольного размера.
по контуру площадки произвольной формы и произвольного размера.
РИС.14-6
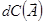 - определяем по каждому бесконечно малому контуру.
- определяем по каждому бесконечно малому контуру.
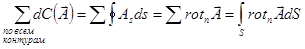 .
.
Циркуляции по всем «внутренним» прямоугольникам встретятся два раза: один раз со знаком «+», второй раз со знаком «-», так что полная циркуляция по контуру 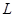 сведется к сумме членов, относящихся к наружным границам площадок:
сведется к сумме членов, относящихся к наружным границам площадок:
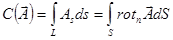 .
.
Полученный результат представляет собой теорему Стокса:
Циркуляция произвольного вектора 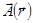 , непрерывного и дифференцируемого во всех точках поверхности
, непрерывного и дифференцируемого во всех точках поверхности 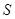 , по замкнутой кривой
, по замкнутой кривой 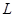 равна потоку ротора этого вектора через поверхность
равна потоку ротора этого вектора через поверхность 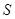 , опирающуюся на кривую
, опирающуюся на кривую 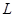 .
.
Форма поверхности 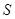 остается неопределенной. Если на один и тот же контур
остается неопределенной. Если на один и тот же контур 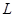 опираются две поверхности
опираются две поверхности  и
и  , то через них проходит одинаковый поток ротора любого вектора
, то через них проходит одинаковый поток ротора любого вектора 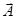 , непрерывного и дифференцируемого на этих поверхностях, равный циркуляции этого вектора по общему контуру
, непрерывного и дифференцируемого на этих поверхностях, равный циркуляции этого вектора по общему контуру 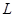 .
.
Примечание. Поток ротора через любую замкнутую поверхность 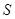 равен нулю, так как для замкнутой поверхности контур стягивается в точку. Следовательно,
равен нулю, так как для замкнутой поверхности контур стягивается в точку. Следовательно,
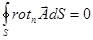 .
.
Математическое отступление закончилось.
Обратимся снова к электростатическому полю.
В силу потенциальности электростатического поля работа по замкнутому контуру равна нулю:
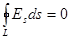 .
.
Воспользовавшись теоремой Стокса, получаем:
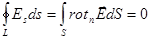 .
.
В силу произвольности выбора замкнутого контура 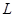 и поверхности
и поверхности 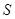 получаем, что направление внешней нормали
получаем, что направление внешней нормали 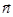 может быть выбрано произвольно. Следовательно:
может быть выбрано произвольно. Следовательно:
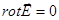
Вспомним, что уравнение Максвелла (2) имеет вид:
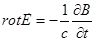 .
.
Отсюда видно, что в отсутствие магнитного поля или в отсутствие магнитного поля, зависящего от времени, мы получаем 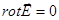 .
.
Будем теперь пользоваться полученными результатами для определения потенциальности векторного поля:
 или
или 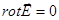 (интегральная форма и дифференциальная форма).
(интегральная форма и дифференциальная форма).
Векторное поле называется потенциальным, если циркуляция вектора напряженности поля по произвольному замкнутому конткру равна нулю или (по теореме Стокса) ротор напряженности поля равен нулю.
Непрерывность тангенциальных составляющих напряженности электрического поля
Ранее мы установили, что нормальная компонента напряженности электрического поля терпит разрыв на заряженной плоскости:
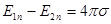 .
.
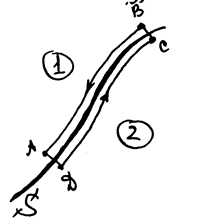 |
Рассмотрим теперь работу сил электростатического поля на замкнутом контуре
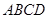 . Если мы выберем расстояния
. Если мы выберем расстояния 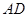 и
и  бесконечно малыми, то работа на этом контуре
бесконечно малыми, то работа на этом контуре 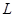
 .
.
РИС.14-7
Отсюда следует 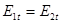 , где
, где 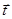 - единичный вектор, лежащий в касательной плоскости к произвольной поверхности
- единичный вектор, лежащий в касательной плоскости к произвольной поверхности 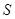 и
и 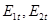 - значения составляющих вектора
- значения составляющих вектора 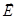 по направлению вектора
по направлению вектора 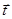 по обеим сторонам поверхности
по обеим сторонам поверхности 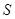 .
.
Если среда 2 – металл, то, так как напряженность поля внутри проводников равна нулю, 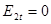 , следовательно, и
, следовательно, и 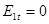 ; следовательно, у поверхности проводников вектор напряженности электрического поля направлен нормально к их поверхности:
; следовательно, у поверхности проводников вектор напряженности электрического поля направлен нормально к их поверхности:
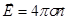 .
.
Потенциал электростатического поля
Для потенциальных и притом только для потенциальных полей можно ввести понятие разности потенциалов.
Разность потенциалов 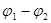 между точками 1 и 2 определяется взятой с обратным знаком величиной работы, совершаемой силами поля над единичным положительным зарядом при перемещении его из точки 1 в точку 2:
между точками 1 и 2 определяется взятой с обратным знаком величиной работы, совершаемой силами поля над единичным положительным зарядом при перемещении его из точки 1 в точку 2:
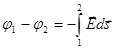 .
.
Естественно, что этот интеграл берется по любому пути между точками 1 и 2.
Примечание. Понятие о разности потенциалов применимо к полю любого вектора, удовлетворяющего условию 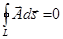 .
.
Поскольку посредством измерения работы можно определить лишь разность потенциалов двух точек, но не сам потенциал, то потенциалу произвольной точки поля 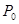 можно приписать любое значение
можно приписать любое значение 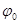 .
.
Тогда потенциал всех прочих точек определяется однозначно. Следовательно, потенциал определяется с точностью до аддитивной постоянной. Обычно за нулевое значение потенциала принимают потенциал бесконечно удаленной точки, 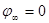 . Тогда для внесения единичного положительного заряда в точку
. Тогда для внесения единичного положительного заряда в точку 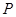 :
:
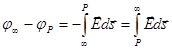 ,
, 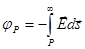 .
.
Потенциал точечного заряда 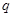 , находящегося в начале координат, в произвольной точке
, находящегося в начале координат, в произвольной точке  :
:
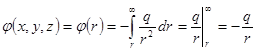 .
.
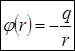 .
.
В системе СИ: 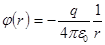 .
.
Электростатический потенциал системы зарядов:
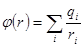 , где
, где 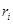 - расстояние от
- расстояние от 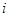 -го заряда до точки наблюдения.
-го заряда до точки наблюдения.
В случае поверхностных зарядов заряд каждой поверхности может быть разложен на совокупность бесконечно малых зарядов элементов поверхности  :
: 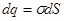 .
.
Переходя от суммирования к интегрированию, находим:
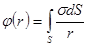 .
.
В поле объемных зарядов 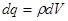 , и потенциал:
, и потенциал: 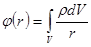 .
.
Примечание. Несмотря на то, что в этих формулах в знаменателе стоит радиус 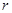 , подинтегральное выражение остается конечным. Легче всего это видно в сферической системе координат - Рис. 14-8.
, подинтегральное выражение остается конечным. Легче всего это видно в сферической системе координат - Рис. 14-8.
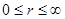 ,
,
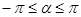 или
или 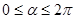 ,
,
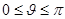 .
.
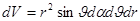 ,
,
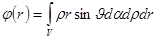 .
.
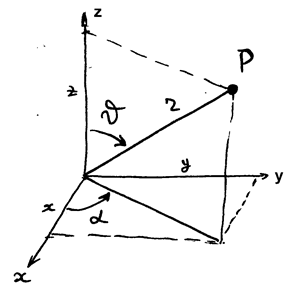 |
РИС.14-8
Единицы измерения потенциала в системах CGSE и SI.
В CGSE:
разность потенциалов между двумя точками, при перемещении между которыми 1 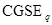 производится работа в 1 эрг – это 1
производится работа в 1 эрг – это 1 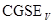 .
.
В SI:
при перемещении между точками с разностью потенциалов 1 В заряда 1 Кл совершается работа в 1 Дж, 1 Дж=1 Кл × 1 В Þ
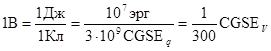 .
.
15 Связь потенциала и напряженности электрического поля
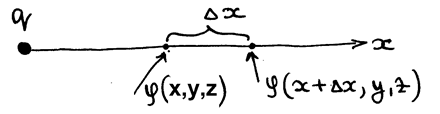 |
РИС.15-1
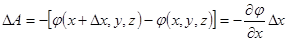 или
или 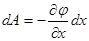 ;
;
с другой стороны, 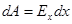 .
.
Отсюда следует, что 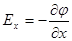 .
.
Аналогично по осям  и
и 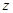 :
: 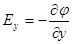 ;
; 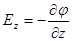 .
.
В векторной форме: 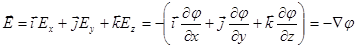 .
.
 =
= 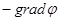 .
.
Сводка операций с векторным оператором 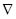 :
:
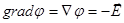 вектор,
вектор,
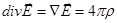 скаляр,
скаляр,
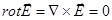 вектор.
вектор.
Мы получили все наиболее важные уравнения электростатики в вакууме – и в интегральной, и в дифференциальной форме.
| Интегральная форма | Дифференциальная форма | |
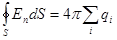
| 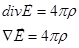
| (1) |

| 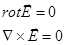
| (2) |

| 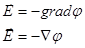
| (3) |
Вообще говоря, выгодно вычислять потенциал (если поле потенциальное), а затем, взяв 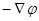 , определить напряженность поля
, определить напряженность поля 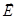 .
.
Сравнивая (1) и (3), находим:
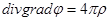 ,
,
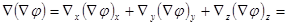
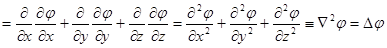 .
.
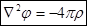 - уравнение Пуассона.
- уравнение Пуассона.
Если нет объемных зарядов, т.е. 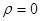 :
:
 - уравнение Лапласа.
- уравнение Лапласа.
Уравнения Лапласа (или Пуассона) вместе с условием 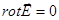 вполне достаточно для решения всех задач электростатики.
вполне достаточно для решения всех задач электростатики.
Потенциал диполя
Применим полученные данные для вычисления потенциала диполя.
Диполем называются два связанных электрических разноименных заряда, находящихся на расстоянии 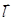 , где вектор
, где вектор 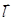 (плечо диполя) направлен от
(плечо диполя) направлен от 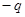 к
к 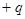 .
.
Момент диполя 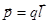 .
.
 |
РИС.15-2
В соответствии с принципом суперпозиции полей:
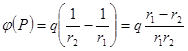 .
.
Если  , то рассматриваемая система зарядов называется точечным диполем.
, то рассматриваемая система зарядов называется точечным диполем.
При выполнении этого условия 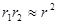 ,
, 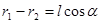 .
.
 , где
, где 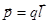 - момент диполя.
- момент диполя.
Напряженность электрического поля диполя
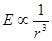 - к нему неприменима электростатическая теорема Гаусса!
- к нему неприменима электростатическая теорема Гаусса!
Термоэлектронный ток между двумя бесконечными плоскими электродами в вакууме.Формула Лэнгмюра.
Полагаем, что при фиксированном  потенциал по
потенциал по  и
и 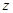 не меняется. Следовательно, эквипотенциальные поверхности – это плоскости, параллельные катоду и аноду.
не меняется. Следовательно, эквипотенциальные поверхности – это плоскости, параллельные катоду и аноду.
Уравнение Пуассона сводится к одномерному:
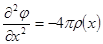 .
.
Так как электрон заряжен отрицательно, плотность объемных зарядов: 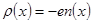 .
.
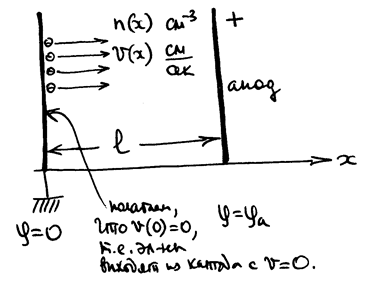 |
РИС.15-3
Теперь уравнение имеет вид:
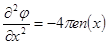 .
.
Поле между электродами совершает работу 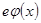 , которая переходит в кинетическую энергию движения электронов:
, которая переходит в кинетическую энергию движения электронов:
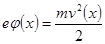 Þ
Þ  .
.
Плотность электронного тока:
 .
.
В стационарном состоянии плотность тока от координат не зависит. Определим отсюда концентрацию электронов:
 и подставим полученный результат в уравнение:
и подставим полученный результат в уравнение:
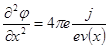 , а сюда подставим
, а сюда подставим 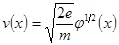 .
.
Получим:
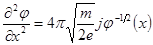 .
.
если обозначить  , то уравнение, которое необходимо решить,
, то уравнение, которое необходимо решить,
 - величины перед
- величины перед 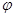 от
от  не зависят.
не зависят.
Решение этого уравнения: 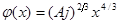 .
.
Можно убедиться в правильности этого решения путем непосредственной подстановки в уравнение.
Граничные условия задачи:
1) Поле вблизи катода равно нулю:  при
при  .
.
2) Катод заземлен (в практических задачах всегда полагают потенциал Земли =0): 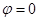 при
при  .
.
3) Потенциал анода: 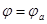 при
при 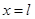 .
.
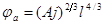 ;
; 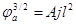 ;
; 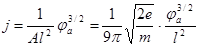 (закон «3/2»).
(закон «3/2»).
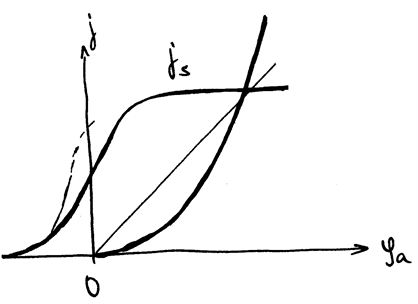 |
РИС.15-4
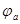 - можно говорить напряжение на аноде, так как потенциал катода равен нулю.
- можно говорить напряжение на аноде, так как потенциал катода равен нулю.
Сдвиг (влево от нуля) обусловлен тем, что вылетающие из катода электроны имеют  , и нужно приложить тормозящее поле, чтобы они не долетели до анода.
, и нужно приложить тормозящее поле, чтобы они не долетели до анода.
Поле в проводниках
Поле внутри проводника равно нулю. Если внутри проводника в какой-либо точке возникает электрическое поле 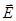 , то возникает упорядоченное движение зарядов, т. е. электрический ток. Носители заряда – электроны (или дырки), отрицательные или положительные ионы.
, то возникает упорядоченное движение зарядов, т. е. электрический ток. Носители заряда – электроны (или дырки), отрицательные или положительные ионы.
Если прохождение тока не связано с переносом вещества, то проводник является электронным, если связано, то ионная проводимость (такова обычно проводимость электролитов, газов, некоторых твердых тел).
В металлах проводимость обычно электронная (или дырочная).
Определение:
Если прохождение тока не связано спереносом массы, то такой проводник называют электронным (дырочным).
Riecke E. (1901 г.): в течение года пропускал электрический ток через три поставленных друг на друга цилиндра - медный, алюминиевый и медный. Количество протекшего электричества было равно 3448800 Кл. Тем не менее цилиндры сохранили свой вес с точностью до
±0,03 мг. Отсюда следует, что металлы обладают электронной проводимостью.
Опытный закон Ома:  . Внутри проводника
. Внутри проводника 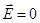 , следовательно,
, следовательно, 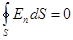 (где
(где 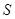 - произвольная замкнутая поверхность внутри проводника). Отсюда по теореме Гаусса
- произвольная замкнутая поверхность внутри проводника). Отсюда по теореме Гаусса 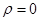 (
( 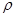 - плотность объемных зарядов), точнее, положительные и отрицательные заряды компенсируются, а все свободные заряды размещаются на границах раздела или на иных неоднородностях.
- плотность объемных зарядов), точнее, положительные и отрицательные заряды компенсируются, а все свободные заряды размещаются на границах раздела или на иных неоднородностях.
Если внутри проводника в какой-либо точке в некоторый момент времени t=t0 возникает электрическое поле E, то сразу возникает упорядоченное движение зарядов: локальный ток. Вследствие этого плотность свободных зарядов уменьшается по закону:
 , где
, где 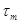 - Максвеллово время релаксации.
- Максвеллово время релаксации.
Максвеллово время релаксации 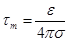 –показывает, в течение какого промежутка времени плотность свободных объемных зарядов уменьшится в e –раз.
–показывает, в течение какого промежутка времени плотность свободных объемных зарядов уменьшится в e –раз.
Если 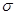 =10-14 Ом-1см-1 (типичный диэлектрик), то это время составляет 3·106 лет. Для металлов –10-12 с. Значит за это время поле в металле уменьшится до нуля.
=10-14 Ом-1см-1 (типичный диэлектрик), то это время составляет 3·106 лет. Для металлов –10-12 с. Значит за это время поле в металле уменьшится до нуля.
Следствие. 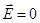 внутри проводника. Но
внутри проводника. Но 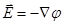 , следовательно,
, следовательно, 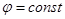 на всем протяжении данного проводника (при отсутствии сторонних эдс). Все части проводника имеют одинаковый потенциал.
на всем протяжении данного проводника (при отсутствии сторонних эдс). Все части проводника имеют одинаковый потенциал.
Внутренняя поверхность металлического шара 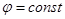 . Значит, внутри полости
. Значит, внутри полости 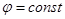 и
и 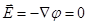 .
.
Дата добавления: 2016-02-24; просмотров: 891;
