Метод электрических изображений
Решение задач электростатики облегчается некоторыми искуственными приемами, в частности, методом электрических изображений.
 |
РИС.15-6
Эквипотенциаль 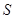 разделяет все пространство на два полупространства I и I’.
разделяет все пространство на два полупространства I и I’.
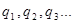 - заряды в полупространстве I,
- заряды в полупространстве I,
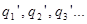 - заряды в полупространстве I’.
- заряды в полупространстве I’.
Сначала вычислили потенциал данной системы точечных зарядов и провели некоторую эквипотенциальную поверхность 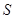 . Теперь поле в I полностью задается распределением зарядов
. Теперь поле в I полностью задается распределением зарядов 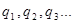 и потенциалом поверхности
и потенциалом поверхности 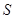 . Поэтому, если вообразить, что поверхность
. Поэтому, если вообразить, что поверхность 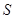 является проводящей (металлической), то поле во всем пространстве не изменится. Однако поля в полупространствах I и I’ становятся независимыми друг от друга.
является проводящей (металлической), то поле во всем пространстве не изменится. Однако поля в полупространствах I и I’ становятся независимыми друг от друга.
В результате мы получаем решение сразу двух задач.
В полупространстве I по одну сторону проводящего тела  находятся точечные заряды
находятся точечные заряды 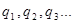 Нужно найти электрическое поле в этом полупространстве. Оно векторно складывается из полей зарядов
Нужно найти электрическое поле в этом полупространстве. Оно векторно складывается из полей зарядов 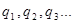 и зарядов, индуцированных на поверхности
и зарядов, индуцированных на поверхности 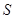 .
.
Однако в силу теоремы единственности поле индуцированных зарядов в полупространстве I эквивалентно полю, создаваемому зарядами 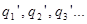 Значит, при вычислении поля в полупространстве I можно поверхность
Значит, при вычислении поля в полупространстве I можно поверхность 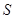 убрать и заменить ее зарядами
убрать и заменить ее зарядами 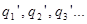
Совокупность этих зарядов называется электрическим изображением зарядов 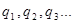 в поверхности
в поверхности 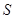 .
.
 |
Пример. Точечный заряд над бесконечной проводящей плоскостью
РИС.15-7

РИС.15-8
.
При таком задании потенциала он обращается в нуль на плоскости 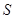 (так как
(так как 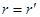 ), следовательно,
), следовательно, 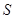 - эквипотенциаль.
- эквипотенциаль.
Теперь начинаем вычислять поверхностную плотность индуцированного заряда (Рис. 15-8)
Осевая симметрия относительно оси 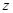 .
.  - симметрична.
- симметрична.
 |
РИС.15-9
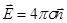 ,
,
 ,
,
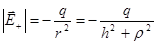 ,
, 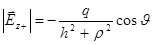 .
.
 ;
;
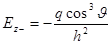 ,
,
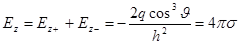 Þ
Þ
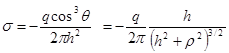 .
.
Проверка: полный индуцированный на поверхности заряд должен быть равен 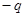 . Убеждаемся в этом путем непосредственного интегрирования.
. Убеждаемся в этом путем непосредственного интегрирования.
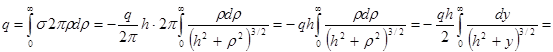
{новая переменная 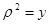 ,
,  }
}
= 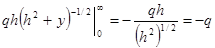 - к чему и стремились.
- к чему и стремились.
Энергия взаимодействия электрических зарядов
При перемещении электрических зарядов силы кулоновского взаимодействия между ними производят некоторую работу 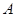 . Эта работа происходит за счет убыли энергии взаимодействия между зарядами:
. Эта работа происходит за счет убыли энергии взаимодействия между зарядами:
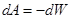 , где
, где 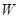 - электрическая энергия.
- электрическая энергия.
 |
Система электрических зарядов обладает потенциальной энергией.
РИС.15-10
Пусть имеется неподвижно закрепленный заряд +q. Если заряд –q отпустить, то он начнет двигаться в сторону заряда  . Потенциальная энергия взаимодействия зарядов перейдет в кинетическую энергию движения
. Потенциальная энергия взаимодействия зарядов перейдет в кинетическую энергию движения 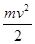 . Вычислим потенциальную энергию взаимодействия двух точечных зарядов при условии, что
. Вычислим потенциальную энергию взаимодействия двух точечных зарядов при условии, что 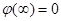 .
.
Итак, неподвижно закреплен заряд 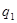 .
.

РИС.15-11
Заряд 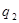 приносим из
приносим из  в поле заряда
в поле заряда 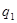 до расстояния
до расстояния 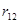 . При этом совершается работа
. При этом совершается работа 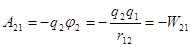 . Здесь
. Здесь  - потенциал, создаваемый зарядом
- потенциал, создаваемый зарядом 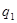 в точке, где находится заряд
в точке, где находится заряд 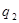 , т.е.
, т.е. 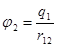 . Если теперь вносим из
. Если теперь вносим из  заряд
заряд 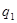 в поле неподвижно закрепленного заряда
в поле неподвижно закрепленного заряда 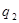 до расстояния
до расстояния 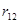 , то совершается работа
, то совершается работа
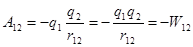 ;
;
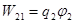 ,
, 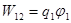 ,
, 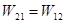 .
.
Энергию взаимодействия двух точечных зарядов можно записать в симметричной форме:
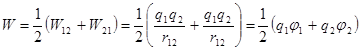 .
.
Собираем систему из трех зарядов
 |
РИС.15-12
В поле заряда 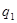 вносим заряд
вносим заряд 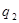 (из
(из  ):
):
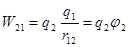 .
.
В систему зарядов  вносим заряд
вносим заряд 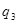 :
:
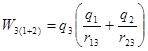 .
.
Полная энергия взаимодействия системы трех зарядов:
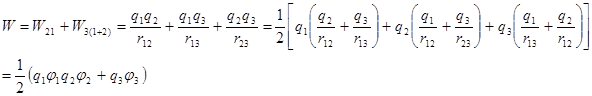
 - потенциал, создаваемый зарядами
- потенциал, создаваемый зарядами 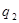 и
и 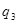 в точке, где находится заряд
в точке, где находится заряд 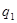 .
.
Вообще 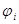 - потенциал, создаваемый в точке, где находится заряд
- потенциал, создаваемый в точке, где находится заряд 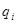 , всеми остальными зарядами.
, всеми остальными зарядами.
Потенциальная энергия взаимодействия  зарядов:
зарядов:
 .
.
Обобщаем полученные результаты на систему объемных и поверхностных зарядов.
Разделяя объемные заряды на элементарные 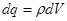 и поверхностные на элементарные
и поверхностные на элементарные 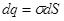 , получаем:
, получаем:
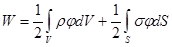 , где
, где 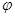 - значение потенциала поля всех объемных и поверхностных зарядов в элементе объема
- значение потенциала поля всех объемных и поверхностных зарядов в элементе объема 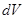 или на элементе поверхности
или на элементе поверхности 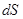 .
.
Несколько простых примеров
1) Энергия уединенного проводника
 |
Пусть проводник изолирован от земли и совсем не заряжен:
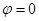 . Затем зарядим до q0.
. Затем зарядим до q0. 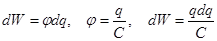 ,
, 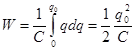 {заряжаем до уровня
{заряжаем до уровня  ,
, 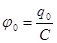 }=
}=
= 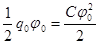 .
.
РИС.15-13
2)
 |
Энергия плоского конденсатора
РИС.15-14
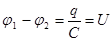 ,
,
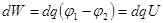 ,
, 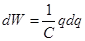 ,
, 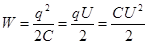 - конденсатор запасает энергию.
- конденсатор запасает энергию.
Понятие о плотности энергии
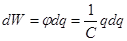 Þ
Þ 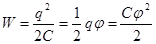 .
.
Рассмотрим простейший случай плоского конденсатора.
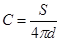 ;
; 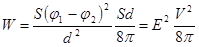 .
.
Этот результат имеет на самом деле весьма общее значение.
Можно показать:
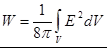 (это получается из
(это получается из 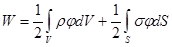 ).
).
Носителем энергии является электрическое поле, энергия локализована в пространстве так, что в единице объема содержится
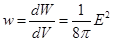 -объемная плотность электрической энергии.
-объемная плотность электрической энергии.
Математическое отступление (теорема Грина)
(дополнительный материал)
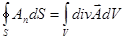 .
.
Обозначим вектор 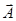 как произведение некоторого скаляра на градиент другого скаляра (
как произведение некоторого скаляра на градиент другого скаляра (  - некоторые функции координат, непрерывные, конечные, имеющие производные первого и второго порядков).
- некоторые функции координат, непрерывные, конечные, имеющие производные первого и второго порядков).
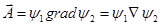 ;
;
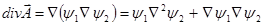 ;
;
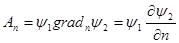 .
.
Подставим полученный результат в формулу, выражающую теорему Гаусса:
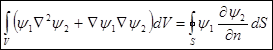 - теорема Грина.
- теорема Грина.
Другая форма записи.
Можно взять 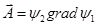 . Получим:
. Получим:
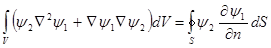 .
.
Вычитая, получим:
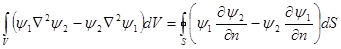 .
.
Здесь 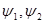 - любые непрерывные конечные скалярные функции координат, обладающие в области интегрирования производными первого и второго порядков.
- любые непрерывные конечные скалярные функции координат, обладающие в области интегрирования производными первого и второго порядков.
Теперь рассмотрим интересующий нас случай энергии взаимодействия:
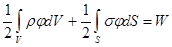 .
.
Положим в теореме Грина  .
.
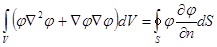 .
.
Вспоминаем: 1)  ,
,
 ;
;
2) 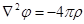 .
.
Подставляя, получаем:
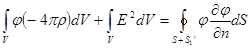 .
.
Поверхность 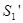 выделяет из объема могущие лежать в нем поверхности разрыва
выделяет из объема могущие лежать в нем поверхности разрыва 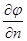
(т. е. заряженные поверхности).
Полагаем, что разрыва потенциала не происходит (т.е. по обе стороны заряженной поверхности 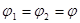 ).
).
Тогда, стягивая поверхность 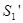 к поверхностям разрыва
к поверхностям разрыва 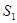 , получим:
, получим:
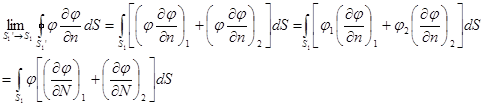
где ранее 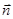 - общая нормаль для
- общая нормаль для  и
и  , т.е. внешняя по отношению к одному
, т.е. внешняя по отношению к одному 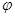 и внутренняя по отношению к другому
и внутренняя по отношению к другому 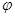 ; теперь
; теперь 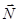 - некая новая нормаль, внешняя по отношению к заряженной поверхности.
- некая новая нормаль, внешняя по отношению к заряженной поверхности.
Тогда 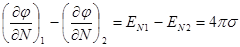 .
.
Итак, при стягивании 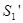 к
к 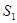 получаем:
получаем:
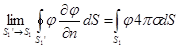 .
.
Соберем теперь полученные результаты.
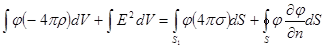 .
.
Делим на  :
:
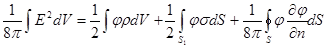 .
.
Распространим теперь интегрирование по области, где существуют объемные и поверхностные заряды, но и по всей области, где существует поле всех этих зарядов. Это означает, что нужно найти такую поверхность, на которой (во всех точках которой) напряженность поля  обращается в 0.
обращается в 0.
В действительности такой замкнутой оболочки, как правило, не существует, и граница поля  .
.
На самом деле нас интересует обращение в нуль некоторых конкретных величин на так называемой границе поля. Обычно интегрируют по бесконечному пространству, но это можно делать в том и только в том случае, если интегралы всех интересующих нас величин по поверхности 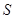 объема стремятся к нулю.
объема стремятся к нулю.
Если 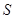 бесконечно возрастает, это значит, что площадь этой поверхности растет как
бесконечно возрастает, это значит, что площадь этой поверхности растет как 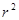 . Следовательно, подинтегральные выражения в интересующих нас поверхностных интегралах должны убывать быстрее, чем
. Следовательно, подинтегральные выражения в интересующих нас поверхностных интегралах должны убывать быстрее, чем 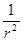 при
при 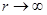 .
.
В нашем случае 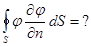
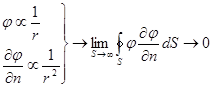 .
.
В дальнейшем будем полагать, что по определению понятия полного поля интегралы по ограничивающей полное поле поверхности 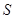 обращаются в нуль.
обращаются в нуль.
Итак:  .
.
 - это бесконечная сумма слагаемых вида
- это бесконечная сумма слагаемых вида 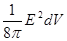 .
.
Итак, носителем энергии является электрическое поле, энергия локализована в пространстве так, что в единице объема содержится:
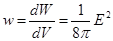 - объемная плотность электрической энергии.
- объемная плотность электрической энергии.
Математическое отступление окончилось.
Появилась некоторая проблема.
Если мы имеем один точечный заряд, то создаваемое им поле  и
и  .
.
Если воспользоваться формулой  , то получим
, то получим  , так как других зарядов, кроме
, так как других зарядов, кроме 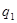 , нет, и никакой потенциал в точке, где он находится, не создается:
, нет, и никакой потенциал в точке, где он находится, не создается: 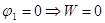 .
.
Дело в том, что формула  учитывает так называемую собственную энергию заряда. Действительно, если бы мы приписали точечному заряду конечный объем, разбили бы его на элементарные заряды
учитывает так называемую собственную энергию заряда. Действительно, если бы мы приписали точечному заряду конечный объем, разбили бы его на элементарные заряды 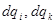 и посчитали бы его энергию по формуле
и посчитали бы его энергию по формуле 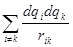 , то получили бы его собственную энергию
, то получили бы его собственную энергию 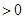 .
.
Собственная энергия заряда – это работа сил взаимного отталкивания, которую они произвели бы, если бы все части заряда разлетелись на  .
.
Полная энергия двух зарядов
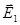 - поле заряда №1,
- поле заряда №1,
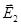 - поле заряда №2,
- поле заряда №2,
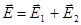 .
.
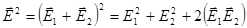 .
.
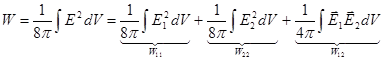 ;
;
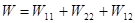 (
( 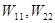 - собственные энергии,
- собственные энергии, 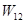 - энергия взаимодействия).
- энергия взаимодействия).
Из 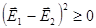 следует, что
следует, что 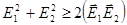 .
.
Следовательно, 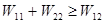 , т.е положительная собственная энергия зарядов всегда больше (или равна) взаимной энергии зарядов, которая может быть как положительной, так и отрицательной. Значит, при всех возможных перемещениях зарядов, не меняющих размеры и формы,
, т.е положительная собственная энергия зарядов всегда больше (или равна) взаимной энергии зарядов, которая может быть как положительной, так и отрицательной. Значит, при всех возможных перемещениях зарядов, не меняющих размеры и формы, 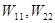 можно считать аддитивными постоянными в выражении для полной энергии
можно считать аддитивными постоянными в выражении для полной энергии 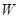 , изменение которой обусловлено изменением взаимной энергии зарядов
, изменение которой обусловлено изменением взаимной энергии зарядов 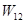 .
.
Энергия электрического поля не обладает свойством аддитивности:
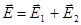 ,
, 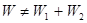 !
!
Дата добавления: 2016-02-24; просмотров: 1393;
