Электродный потенциал. Уравнение Нернста.

Учение об электродвижущих силах гальванических элементов является одним из основных разделов электрохимии. Начало изучению электродвижущих сил бы­ло положено еще М. В. Ломоносовым (1750), который в своих работах отмечал связь между химическими и электрическими явлениями. Позднее наблюдения итальянского физиолога Гальвани (1780) и обширные работы итальянского физи­ка Вольта (1780) привели к открытию гальванических элементов.

В 1800 г. Вольта изобрел первый химический источник тока, так называемый вольтов столб, который был собран из пластинок различных металлов, разделен­ных прослойками ткани, смоченной электролитом. Исследования привели Вольта к открытию контактной разности потенциалов, возникающей при соприкосновении металлов различной природы. В первых исследованиях в качестве чувствительного прибора для обнаружения малой разности потенциалов ученый использовал свежеанатомированные мышцы лягушки. Этот случай является наглядным примером того, как биологические методы исследования нередко могут способствовать ус­пешному развитию физики и других точных наук.

Открытие химических источников тока и контактной разности потенциалов оказало большое влияние на все последующее развитие электрохимических явле­ний. В настоящее время методы электрохимии получили широкое распростране­ние в агрохимии, физиологии растений, в биологии, почвоведении, а также во мно­гих других смежных дисциплинах.

Если в чистую воду погрузить пластинку какого-либо металла, то согласно гидратной теории Д. И. Менделеева ионы металла бу­дут взаимодействовать с полярными молекулами воды. Иными сло­вами, поверхностно расположенные катионы этого металла будут гидратироваться молекулами воды и переходить в окружающий раствор, заряжая его положительно, т. е. металл будет как бы рас­творяться (рис.4.8).

Однако электроны, в избытке остающиеся в металле, заряжают его поверхностный слой отрицательно. В результате этого между ионами металла, перешедшими в раствор, и поверхностью металли­ческой пластинки возникают силы электростатического притяже­ния, в силу чего ионы, окружающие пластинку, образуют так назы­ваемый двойной электрический слой, схема которого приведена на рис. 4.8. Этот слой препятствует дальнейшему растворению металла и в системе устанавливается подвижное равновесие, которое харак­теризуется равными скоростями как растворения, так и обратного осаждения ионов из раствора на поверхности металлической пла­стинки.

Первоначально считали, что двойной электрический слой имеет плоское строение. Он уподоблялся конденсатору, одна из обкладок которого расположена на поверхности металла, другая — в слое прилегающей к электроду жидкости. Расстояние между обкладками равно диаметру молекулы.

Согласно этой теории, которую обычно связывают с именем Гельмгольца (1879), учитывалось только прояв­ление электростатических сил взаимодействия между зарядами про­тивоположного знака и не учитывалось изменение свойств двойного электрического слоя с изменением концентрации электролита и его температуры, что явилось основным недостатком теории Гельм­гольца.

В разработке современной теории строения двойного электриче­ского слоя на границе твердая фаза—жидкость и методов его ис­следования ведущая роль принадлежит А. Н. Фрумкину и его шко­ле. Работы А. Н. Фрумкина и его учеников установили, что слой ионов, располагающийся в жидкости, благодаря действию двух про­тивоположно направленных сил (электростатического притяжения и теплового движения) имеет диффузное строение, т. е. он проника­ет в жидкость на некоторую глубину (рис. 4.8).

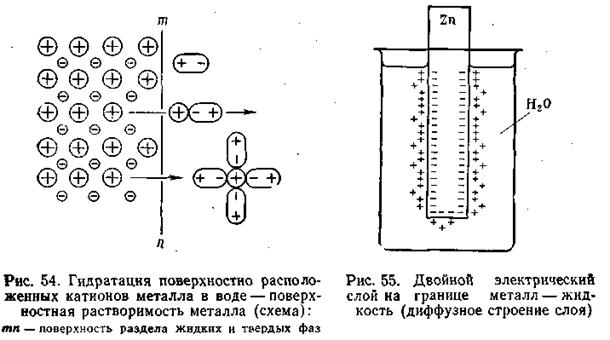
Определенная часть ионов удерживается вблизи поверхности раздела металл—электролит, образуя обкладку двойного слоя с толщиной, отвечающей среднему радиусу ионов электролита. Ос­тальные ионы, входящие в состав двойного слоя, распределяются диффузно, с постепенно убывающей плотностью заряда.

Таким образом, при соприкосновении металла с водой ионы его находятся под действием двух конкурирующих сил: электростати­ческого притяжения, возникающего между ионами металла и моле­кулами воды (явление гидратации), и электростатического притя­жения со стороны электронного газа, определяющего прочность кристаллической решетки.

Вполне понятно, что чем прочнее кристаллическая решетка ме­талла, тем труднее иону металла перейти в раствор. Чем выше величина энергии гидратации, тем с большей жадностью молекулы воды взаимодействуют с этими ионами, и тем легче им выделиться в рас­твор.

В результате взаимодействия двух указанных взаимно противо­положных сил растворение металла в воде приобретает характер только поверхностного процесса и охватывает лишь очень узкую об­ласть на границе металл—жидкость. В этом поверхностном слое концентрация ионов металла, несмотря на его чрезвычайно малую растворимость, может быть довольно значительной. Кроме того, в поверхностном растворе гидратированные катионы в силу электро­статических сил притяжения со стороны электронов кристалличе­ской решетки металла совершают лишь ограниченное кинетическое движение в виде так называемых «пристенных» скачков. Они проч­но связаны с жестким каркасом кристаллической решетки металла.

Таким образом, в системе металл — вода на границе раздела фаз возникает двойной электрический слой, блокирующий поверх­ность металла. Образовавшаяся пограничная разность потенциалов получила название электродного потенциала (дат. potentia — воз­можность, мощь).

Если жидкая среда — чистая вода, для всех металлов картина в качественном отношении будет однозначной: металл заряжается от­рицательно, прилегающий слой жидкости — положительно. Однако количественно для разных металлов будут наблюдаться существен­ные различия, что объясняется не только неодинаковой энергией связи катионов этих металлов в кристаллической решетке, но и не­одинаковой гидратируемостью этих катионов.

Несколько иная картина наблюдается в случае, если металличе­скую пластинку погрузить не в чистую воду, а в раствор соли этого металла. При этом могут иметь место три случая.

1. Исходная концентрация ионов данного металла в растворе С меньше концентрации С_о, соответствующей равновесному состоянию ионов после погружения в раствор металлической пластинки, т. е. С<С₀. При этом будут происходить оба процесса — переход метал­ла в раствор

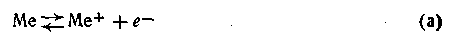
и выделение металла из раствора -

Поскольку С<Со, преобладающим будет процесс (а), т. е. вы­деление электронов превысит их поглощение. В результате этого поверхность металлической пластинки зарядится отрицательно, а прилегающий слой раствора — положительно.

2. Концентрация ионов металла С больше равновесной концен­трации С₀, т. е. С>С₀. В этом случае наблюдается обратное явле­ние: ионы металла из раствора выделяются на поверхности метал­лической пластинки. Чтобы ионы металла могли выделиться, они должны присоединить электроны согласно уравнению (б). Посколь­ку источника электронов в системе нет, выделение металла на поверхности пластинки происходит в виде ионов. В результате поверх­ность приобретает положительный заряд.

3. При условии С=С₀ вся система будет находиться в состоянии подвижного равновесия, разность потенциалов между жидкостью и металлом равна нулю. В этом случае из раствора осаждается на единицу поверхности металла столько же катионов, сколько их вы­ходит в двойной электрический слой.

Принимая это во внимание, нетрудно найти математическую за­висимость между величиной скачка потенциала на границе сопри­косновения металла и раствора и концентрацией (точнее, актив­ностью) ионов этого металла в растворе.

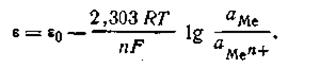
4.84

Так как активность металла принимается равной единице (а_Mе= 1), то с учетом этого уравнения (4.84) будет иметь следующее выражение:

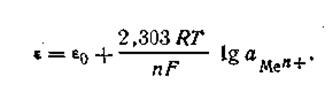
4.85

Уравнение (4.85) называется уравнением Нернста,

ε₀— постоянная величина, характеризующая электрохимическую природу электрода.

Для расчетов удобнее предварительно вычислить значение R·T· 2,303/F при какой-либо температуре. Например, при 291 К это число будет равно 0,0577. Следовательно, для температуры 291 К уравнение Нернста будет иметь вид:

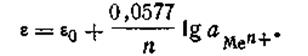
4.86

Обозначим численное значение выражения R·T·2,303/F буквой Ж.

Зависимость этого числа от температуры выразится следующей формулой:

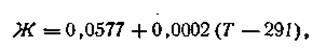
4.87

где Г —любая температура, при которой производится измерение разности потенциалов. С учетом этого обозначения уравнение элек­тродного потенциала Нернста будет иметь следующий вид:

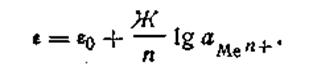
4.88

Каков же физический смысл ε_о в уравнении электродного потен­циала Нернста? Несложный математический анализ этого уравне­ния показывает, что при С=1 моль/л все выражение

обращается в нуль, и тогда

4.89

Таким образом, стандартным (нормальным) потенциалом назы­вается такой потенциал, который возникает на металлической плас­тинке, находящейся в контакте с одноименными ионами в растворе, с концентрацией С=1 моль/л.

За нулевую точку измерения потенциалов условно принят нор­мальный потенциал водородного электрода. Для изготовления его используют способность платины растворять га­зообразный водород. Платиновая проволока или пластинка, содер­жащая растворенный водород, играет роль «водородной пластинки», а функции «раствора солей» может выполнять любой водный раствор, в котором всегда присутствуют ионы водорода Н⁺. Причем нормальный потенциал водородного электрода равен нулю при ус­ловии, что давление молекулярного водорода на пластинке равно 101,325 кПа и С_Н+ = 1 моль/л.

Если нормальный потенциал какого-либо металла больше во­дородного, его принято считать положительным, если меньше — от­рицательном.

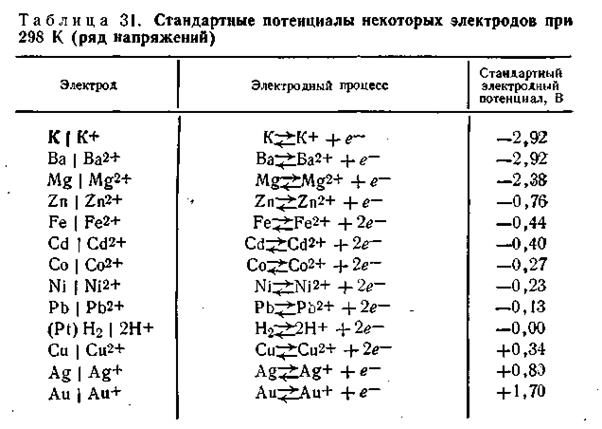
Если все металлы расположить последовательно по возраста­ющей величине их нормальных электродных потенциалов, получит­ся ряд напряжений. В табл. 4.9 приведены стандартные потенциалы некоторых металлов.

В этой таблице каждый электрод обозначен символом элемента, из которого он состоит, и соответствующего иона, а вертикальная линейка изображает поверхность раздела двух фаз, где имеет место скачок потенциала.

Представленным в табл. 4.9 рядом напряжений широко пользу­ются в практике при составлении так называемых гальванических элементов, а также при изучении взаимодействия между металлами и кислотами, между солями и металлами. Зная ряд напряжений, можно предвидеть направление реакции вытеснения одних элемен­тов другими. Так металлы, стоящие в ряду напряжений после водо­рода, не способны вытеснять водород из кислот. Вытеснение метал­ла из солей другим металлом осуществляется только в том случае, если вытесняющий металл расположен в ряду напряжений до вытес­няемого.

Например, при составлении гальванического элемента из цинка и свинца в качестве положительного электрода следует взять свин­цовый (ε_о= -0,13 В), а в качестве отрицательного — цинковый (ε_о= -0,76 В).

Электроды подразделяются на электроды первого и второго ро­да. Электроды первого рода — это электроды из металла, погружен­ного в раствор, содержащий ионы того же металла (например, Cu|Cu²⁺, Zn|Zn²⁺). Эти электроды обратимо обменивают катионы Ме↔Меⁿ⁺nе, где n — число теряемых (или приобретаемых) электронов (е^-).

Электроды второго рода состоят из металла, покрытого слоем труднорастворимой соли и погруженного в раствор какой-либо лег­корастворимой соли с тем же анионом. Такие электроды обратимы относительно этого аниона.

Для электродов второго рода выражение электродного потенциала

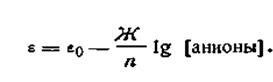
4.90