Треугольное распределение
Треугольное характеризует случайные величины, имеющие ограниченную область возможных значений (tн, tk). Положение и форму треугольного распределения характеризуют три параметра: tн, tk – границы области возможных значений; tм – мода (рис. 9).
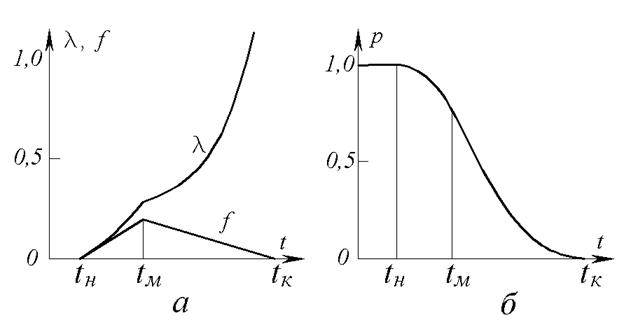 Рис. 9. Треугольное распределение случайной величины: a – графики плотности распределения f(t) и интенсивности отказов; λ(t); б – график функции надежности p(t)
Рис. 9. Треугольное распределение случайной величины: a – графики плотности распределения f(t) и интенсивности отказов; λ(t); б – график функции надежности p(t)
Если обозначить значение плотности распределения в точке моды f(tм)=h, тo 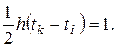
Плотность распределения
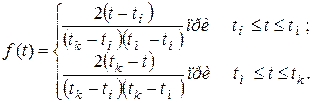
Функция надежности
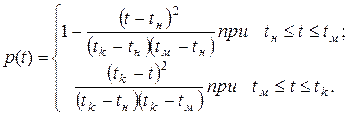
Интенсивность отказов
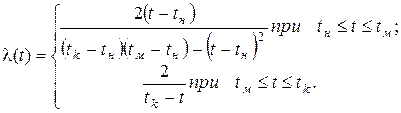
В некоторых задачах удобно использовать в качестве параметров распределения также скорости изменения плотности распределения
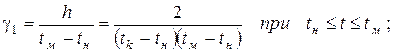
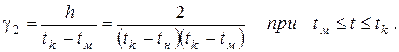
Медиана tме треугольного распределения может быть найдена из уравнения
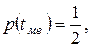
в результате решения которого получим
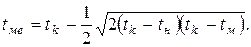
Математическое ожидание
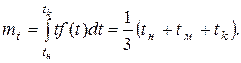 (35)
(35)
Применив подстановку 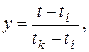 можно перейти к нормированному треугольному распределению. При этом tн соответствует yн = 0, tkсоответствует yk = 1.
можно перейти к нормированному треугольному распределению. При этом tн соответствует yн = 0, tkсоответствует yk = 1.
Обозначим:
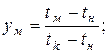
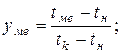
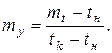
После преобразований получим:
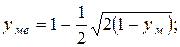
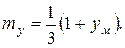
Функция надежности может быть выражена через вспомогательную функцию ФΔ(y).следующим образом:
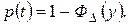 (36)
(36)
где ФΔ(y) – нормированная функция распределения;
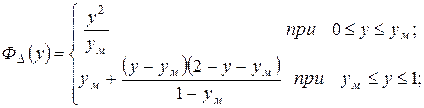 (37)
(37)
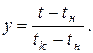
На рис. 10 приведены графики ФΔ (y) при различных значения параметра yм. Значения функции ФΔ(y) надежности, соответствующие определенным tн, tм, tк, можно также вычислить но табл. 1.
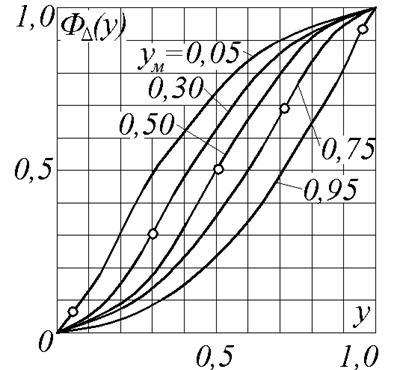
Рис.1.10. Значения нормированной функции распределения ФΔ (y). Точками на кривых отмечены значения ФΔ(y)= yм
Таблица 1
| у | yм | ||||||||||
| 0,05 | 0,10 | 0,20 | 0.30 | 0,40 | 0,50 | 0,60 | 0,70 | 0,80 | 0,90 | 0,95 | |
| 0,05 | 0,050 | 0,025 | 0,012 | 0,008 | 0,007 | 0,005 | 0,004 | 0,034 | 0,003 | 0,003 | 0,003 |
| 0,10 | 0,147 | 0,100 | 0,050 | 0,033 | 0,025 | 0,020 | 0,017 | 0,014 | 0,013 | 0,011 | 0,011 |
| 0,20 | 0,326 | 0,289 | 0,200 | 0,133 | 0,100 | 0,080 | 0,067 | 0,057 | 0,050 | 0,044 | 0,042 |
| 0,30 | 0,484 | 0,456 | 0,387 | 0,300 | 0,225 | 0,180 | 0,150 | 0,129 | 0,113 | 0,100 | 0,095 |
| 0,40 | 0,621 | 0,400 | 0,560 | 0,486 | 0,400 | 0,320 | 0,267 | 0,229 | 0,200 | 0,178 | 0,168 |
| 0,50 | 0,737 | 0,722 | 0,688 | 0,643 | 0,583 | 0,500 | 0,417 | 0,357 | 0,313 | 0,278 | 0,263 |
| 0,60 | 0,832 | 0,822 | 0,800 | 0,771 | 0,733 | 0,680 | 0,600 | 0,514 | 0,450 | 0,400 | 0,379 |
| 0,70 | 0,905 | 0,900 | 0,888 | 0,871 | 0,850 | 0,820 | 0,775 | 0,700 | 0,613 | 0,544 | 0,516 |
| 0,80 | 0,978 | 0,956 | 0,950 | 0,943 | 0,933 | 0,920 | 0,900 | 0,867 | 0,800 | 0,711 | 0,674 |
| 0,90 | 0,989 | 0,969 | 0,987 | 0,986 | 0,983 | 0,980 | 0,975 | 0,937 | 0,950 | 0,900 | 0,853 |
| 0,95 | 0,997 | 0,997 | 0,997 | 0,996 | 0,996 | 0,995 | 0,993 | 0,992 | 0,988 | 0,975 | 0,950 |
Дата добавления: 2015-12-01; просмотров: 4203;
