Применение формулы полной вероятности при расчете надежности систем
При использовании формулы полной вероятности учитываются гипотезы H1, Н2, …, Нп – несовместимые события, образующие полную группу. Вместе с одним из этих событий может произойти рассматриваемое событие Х – безотказная работа системы в течение заданной наработки (0, ti). Вероятность появления события Х равна сумме произведений вероятности каждой гипотезы Р(Нj) на условную вероятность P(X|Hj) события при этой гипотезе:
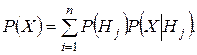 (46)
(46)
При использовании формулы полной вероятности для расчета надежности выбирается определенная группа элементов логической схемы, и формируются гипотезы о том, что же произошло с этой группой элементов в течение заданной наработки. Гипотезы могут являться сложными событиями. В каждой из гипотез учитывается, что для любого элемента рассматриваемой группы возможными исходами являются либо безотказная работа, либо отказ.
При вычислении условной вероятности безотказной работы системы P(X|Hj) при гипотезе Нj предполагается, что произошли соответствующие события – (безотказная работа или отказ одного или нескольких элементов) и рассматриваются соответствующие условные логические схемы.
В качестве примера применения формулы полной вероятности рассмотрим расчет надежности системы, логическая схема, для расчета надежности которой приведена на рис. 11.
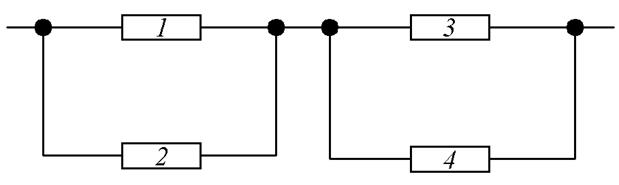
Рис. 11. Логическая схема для расчета надежности системы.
Рассмотрим группу из первого и третьего элементов. Здесь возможны четыре гипотезы о состояниях элементов: оба элемента остались работоспособными; первый элемент отказал, второй остался работоспособным; первый элемент остался работоспособным, третий отказал; оба элемента отказали. Гипотезы и соответствующие им вероятности приведены в табл. 2. Цифрой 1 обозначены работоспособные состояния элементов, цифрой 0 – неработоспособные.
Таблица 2
| Гипотеза | Что произошло с элементами | Вероятность гипотезы P(Hj) | Условная вероятность безотказной работы системы при гипотезе Нj P(X|Hj) | |
| H1 | p1·p3 | |||
| H2 | (1-p1)p3 | p2 | ||
| H3 | p1(1-p3) | p4 | ||
| H4 | (1-p1) (1-p3) | p2·p4 |
Подставив выражения для P(Hj) и P(X|Hj)в (46), получим после преобразований выражение для вероятности безотказной работы системы:
pc=p1p3+(1–p1)p3p2+p1(1–p3)p4+(1–p1)(1–p3)p2p4=p1p3+p2p3+p1p4+p2p4–
–(p1p2p3+p1p3p4+p1p2p4+p2p3p4)+p1p2p3p4.
В ряде случаев удобно применять формулу полной вероятности для вычисления вероятности отказа рассматриваемой системы.
В любом случае цель применения формулыполной вероятности – сокращение объема математических образований и вычислений.
Дата добавления: 2015-12-01; просмотров: 2084;
