Гамма-распределение
Плотность гамма-распределения
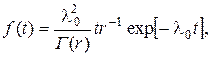 (28)
(28)
где 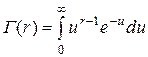 – гамма-функция.
– гамма-функция.
В теории надежности гамма-распределение обычно используется при целом r. При r=1 получается показательное распределение. В данном случае показательное распределение – это распределение наработки до первого отказа. При целом r>1 гамма-распределение является распределением суммы r независимых случайных величин, каждая из которых имеет показательное распределение с параметром 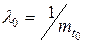 . Гамма-распределение при целом r иногда называют распределением Эрланга. Для такого распределения
. Гамма-распределение при целом r иногда называют распределением Эрланга. Для такого распределения
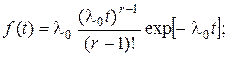 (29)
(29)
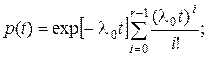 (30)
(30)
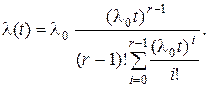 (31)
(31)
Матёматическое ожидание наработки до отказа
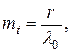
дисперсия
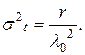
Графики гамма-распределения приведены на рис. 7.
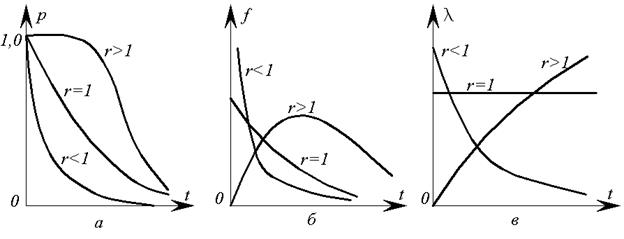
Рис. 7. Графики гамма-распределения. а – функции надежности; б – кривые распределения наработки до появления r отказов; в – интенсивности отказов.
При больших r гамма-распределение сходится, к нормальному распределению с параметрами
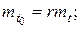
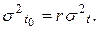
В качестве примера использования гамма-распределения представим себе резервированную систему, состоящую из r одинаковых элементов, причем под нагрузкой находится один элемент, а остиальные поочередно автоматически включаются в работу после отказа работающего элемента. При показательном распределении наработки до отказа элементов суммарная наработка системы будет подчинена гамма-распределению.
Дата добавления: 2015-12-01; просмотров: 1456;
