Показатели надежности неремонтируемых объектов

Такие объекты работают, до первого отказа. Для оценки надежности неремонтируемых объектов используют вероятностные характеристики случайной величины – наработки до отказа T. Под наработкой понимают продолжительность или объем работы объекта, измеряемые в часах, километрах, гектарах, циклах, кубометрах или в других единицах. Когда наработку выражают в единицах времени, иногда используют термин «время безотказной работы», или, что то же самое, «время до появления отказа».

Полной характеристикой любой случайной величины является ее закон распределения, т. е. соотношение между возможными значениями случайной величины и соответствующими этим значениям вероятностями. Распределение наработки до отказа может быть описано с помощью различных показателей надежности неремонтируемых изделий. К числу таких показателей относятся:

· функция надежности р(t);

· плотность распределения наработки до отказа f(t);

· интенсивность отказов λ(t).

Функцией надежности называют функцию, выражающую вероятность того, что Т – случайная наработка до отказа объектов - будет больше заданной наработки (0, t), отсчитываемой от начала эксплуатации, т. е.

p(t) =P (T ≥t).

Перечислим некоторые очевидные свойства р(t):

1) р(0) =1, т. е. можно рассматривать безотказную работу лишь тех объектов, которые были работоспособны в момент включения;

2) p(t) является монотонно убывающей функцией заданной наработки t;

3) p(t) → 0 при t → ∞ т. е. любой объект со временем откажет.

Наряду с p(t) используется и функция ненадежности:

q(t)=1–p(t)=P{T<t}.

Она характеризует вероятность отказа объекта на интервале (0, t). Функция ненадежности является функцией распределения случайной величины T; Эта функция иногда обозначается F(t).

На рис. 2 приведены графики одной из возможных функций надежности p(t) и соответствующей функции q(t).

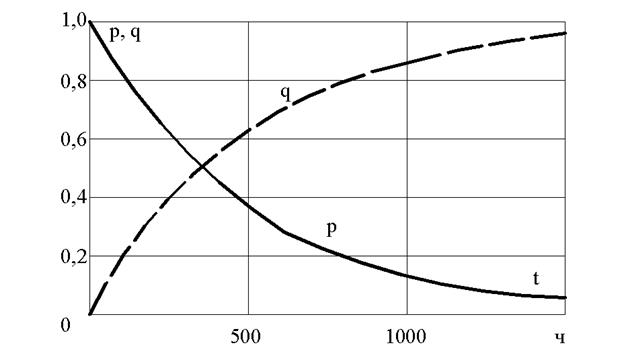
Рис 1.2. Функции надежности p(t) и ненадежности q(t) объекта.

Во многих задачах в качестве показателя надежности используется вероятность безотказной работы – вероятность того, что в пределах заданной наработки не возникает отказа объекта. При этом обычно имеют в виду условную вероятность p(t₁, t₂) безотказной работы в течение наработки от t₁ до t₂ при условии, что в момент времени t₁ объект был работоспособным. Эту условную вероятность можно определить по функции надежности.

Рассмотрим два интервала (0, t₁) и (t₁, t₂). Событие, состоящее в безотказной работе в течение интервала (0, t₂) является совмещением двух событий:

1) объект безотказно работал на интервале (0, t₁);

2) оставшийся работоспособным к моменту t₁ объект безотказно проработал на интервале (t₁, t₂).

Поэтому согласно правилу умножения вероятностей

p(t₂) = p(t₁) p(t₁, t₂)

следовательно

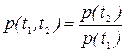(1)

Таким образом, условная вероятность безотказной работы на интервале (t₁, t₂) равна отношению значений функции надежности в конце и в начале интервала.

Надежность малых неремонтируемых объектов не всегда удобно характеризовать вероятностью безотказной работы, так как для небольших периодов заданной наработки значения p(t₁, t₂) будут близкими к единице. Поэтому наряду с р(t) используются и другие показатели надеж­ности, например плотность распределения наработки до отказа

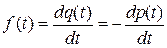(2)

Плотность распределения наработки до отказа f(t) является дифференциальной формой закона распределения наработки до отказа. Плотность f(t) является неотрицательной функцией, причем

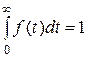
График f(t) часто называют «кривая распределения наработки до отказа».

В соответствия с (2) функция надежности и функция ненадежности связаны с f(t) соотношениями

;

.

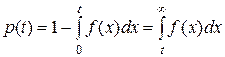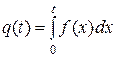Величина f(t)dt характеризует вероятность отказа за интервал наработки (t, t+dt) объекта, взятого наугад из множества одинаковых объектов. При этом неизвестно, работоспособен ли, этот объект к началу интервала (т. е. в момент t) или отказал ранее. Это не всегда удобно на практике, и f(t) как самостоятельный показатель надежности неремонтируемых объектов находит ограниченное применение. Чаще применяют интенсивность отказовλ(t) – условную плотность вероятности возникновения отказа неремонтируемого объекта, определяемую для рассматриваемой наработки при условии, что до этой наработки отказ не возник. Интенсивность отказов можно рассматривать как относительную скорость уменьшения значений функции надёжности с увеличением интервала (0, t). Чтобы пояснить смысл этой характеристики, проведем следующие рассуждения.

Введем хорошо согласующееся с практикой предположение о том, что вероятность o(t) появления двух и более отказов за бесконечно малый интервал наработки (t, t+dt)убывает быстрее, чем длина этого интервала, т. е. o(t) является бесконечно малой более высокого порядка, чем dt. Иными словами, если имеется группа одинаковых объектов,товероятность того, что в одно и тоже мгновение откажет сразу несколько одинаковых объектов очень мала. Таким образом, из рассмотрения исключаются такие явления, как катастрофы и стихийные бедствия.

Рассмотрим два смежных интервала наработки (0, t) и (t, t+dt). Для того чтобы некоторый объект имел возможность отказать в интервале наработки (t, t+dt), он должен безотказно работать в течение (0, t). Согласно правилу умножения вероятностей вероятность отказа объекта в течение наработки (t, t+dt)

q (t, t+dt) = f(t)dt=p(t)z, (3)

где p(t) – вероятность безотказной работы объекта в течение наработки (0, t), т. е. значение функции надежности; z – условная вероятность отказа объекта за малую наработку (t, t+dt), найденная в предположении, что он безотказно проработал интервал (0, t).

Условную вероятность отказа объекта в течение наработки(t, t+dt) в предположении его безотказной работы до момента t обычно выражают формулой

z=λ(t)dt,

где величина λ(t)называется интенсивностью отказов.

Таким образом, при использовании λ(t)рассматривается лишь остающиеся работоспособными к моменту объекты, отказавшие исключаются из рассмотрения.

Из (2) и (3) получаем:

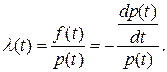(4)

Решение уравнения (4) при начальном условии р(0) = 1 дает для функции надежности формулу

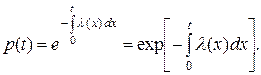(5)

При λ = const формула (5) существенно упрощается:

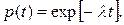(6)

Вероятность безотказной работы в течение наработки (t₁, t₂) объекта, который был работоспособным к началу этого интервала,

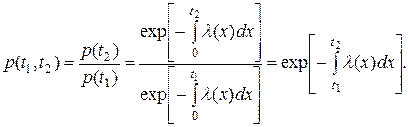(7)

При λ =const вероятность безотказной работы в течение наработки (t₁, t₂) не зависит от возраста объекта:

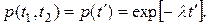(8)

где t'=t₂ –t₁.

При λt'<< 1обычно полагают:

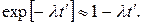
В качестве показателей надежности неремонтируемых объектов применяют также числовые характеристики случайной наработки до отказа. Их обычно легче определить по экспериментальным данным, чем p(t), λ(t), f(t). Наиболее часто используют среднюю наработку до отказа (математическое ожидание наработки до отказа).

Согласно определению математического ожидания непрерывной неотрицательной случайной величины

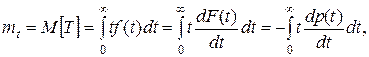
где F (t) – функция распределения случайной величины Т.

Интегрируя по частям, получаем:

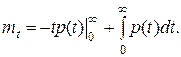
Первое слагаемое в этом равенстве

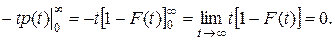
Это можно пояснить следующими рассуждениями. Если неотрицательная случайная величина Т имеет конечное математическое ожидание, т. е. интеграл 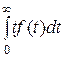cxoдится, то интеграл 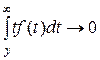при у→ ∞.

Так как

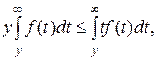
то при у→ ∞

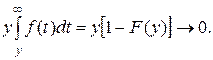
Следовательно

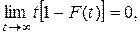
и средняя наработка до отказа

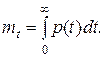(9)

Таким образом, средняя наработка до отказа численно равна площади под кривой p(t).

При λ =const имеем

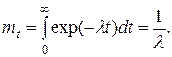
Подставив в (6) значение t=m_t =1/λ, получим, что при λ = const среднюю наработку до отказа можно по­нимать как наработку t = m_t, в течение которой объект остается работоспособным с вероятностью р(t=m_t)=ехр(-1)≈0,37.

Для малых неремонтируемых объектов, например элементов интегральных микросхем, средняя наработка до первого отказа является понятием условным, так как обычно они не эксплуатируются столь долго и устаревают гораздо раньше, чем успевают наработать m_t .

Значения m_t обычно вычисляются по экспериментальным данным об отказах элементов в начальный период их эксплуатации. Поэтому m_t можно понимать как среднюю наработку до отказа, которая имела бы место в действительности, если бы элемент сохранял в течение всего периода использования ту интенсивность отказов, которой он обладал в начальный период эксплуатации или на испытаниях.

На практике представляют интерес две условные средние наработки неремонтируемых объектов:

1) средняя полезная наработка 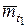при условии, что при достижении наработки t₁ все оставшиеся работоспособными объекты снимаются с эксплуатации;

2) средняя продолжительность предстоящей работы 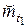при условии, что объект безотказно работал на интервале (0, t₁).

При вычислении средней полезной наработки 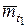учтем, что p(t₁)∙100% объектов безотказно проработают на интервале (0, t₁), а остальные откажут на этом интервале.

Согласно определению математического ожидания имеем:

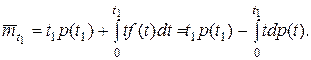
Интегрируя по частям, получаем:

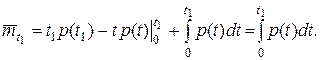(10)

При вычислении условной средней продолжительности предстоящей безотказной работы имеем:

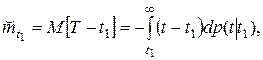(11)

где 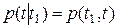– условная вероятность безотказной работы в течение наработки (t₁, t) при условии, что в момент времени t₁ объект работоспособен. В соответствии с (1)

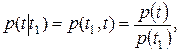
поэтому

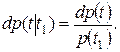(12)

Подставляя (12) в (11) и интегрируя по частям, получаем:

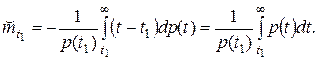(13)

Учитывая (9), (10) и (13), получаем соотношение между средними наработками

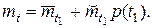(14)

Это соотношение иллюстрирует рис. 1. 3. При λ =const имеем:

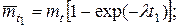
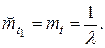
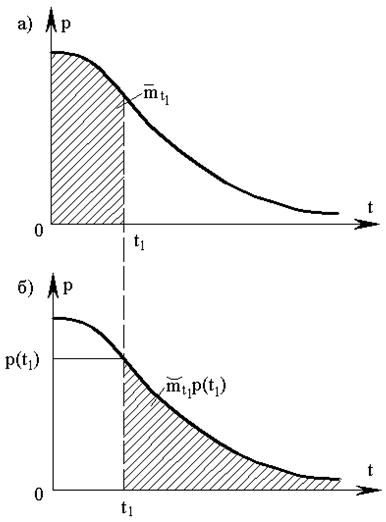
Рис. 3. К вопросу о вычислении условных средних наработок. а) – полезная средняя наработка 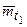; б) – средняя продолжительность предстоящей безотказной работы .

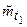При оценке параметрической, т. е. по постепенным отказам, надежности целесообразно учитывать стратегию замен рассматриваемых объектов. Если производятся индивидуальные замены, т. е. каждый конкретный объект из множества одинаковых эксплуатируется до отказа, то используют рассмотренные выше показатели надежности.

При второй стратегии (групповые замены) эксплуатация всех объектов данного типа прекращается при достижении назначенного ресурса (заданной суммарной наработки). В течение назначенного ресурса должны практически отсутствовать параметрические отказы из-за старения, изнашивания и других причин. Иначе говоря, назначенный ресурс должен быть меньше наработки t_н до начала массовых параметрических отказов.

Возможны различные определения t_н. Наиболее общее состоит в том, что величина t_н равна суммарной наработке от начала эксплуатации, при которой плотность распределения f(t) ≈ λ(t) впервые достигает критического значения f_кр≈λ_кр. При этом неявно учитывается известный из опыта эксплуатации факт: для параметрических отказов из-за старения, изнашивания и других нестационарных процессов при t=0 всегда f(0) =λ(0) = 0.

Так как распределение наработки до появления параметрического отказа обычно является унимодальным, то величину f_кр≈λ_кр удобно задавать в долях от моды f(t_М), например f_кр=0,01f(t_М).

Другие определения t_н основаны на рассмотрении особенностей левой ветви теоретического распределения наработки до параметрического отказа. Здесь величина t_н уже не связана с достижением определенного значения f_кр≈λ_кр.