Число состояний. Плотность состояний
В классической физике состояние частицы определяется заданием трех координат Х, У, Z и трех проекций импульса на оси координат рх, ру, рz.
Если рассмотреть 6-мерное пространство с осями координат Х, У, Z, рх, ру, рz , то состояние частицы в нем в любой момент времени определяется фазовой точкой с координатами Х, У, Z, рх, ру, рz.
Такое пространство называют фазовым. Элемент этого фазового пространства координат обозначим
DГV = dx dy dz.
Элемент объема фазового пространства импульсов обозначим
DГр = dрх dру dрz.
У квантовых частиц различным элементам объема шестимерного фазового пространства отвечают различные квантовые состояния микрочастицы, если размер этих элементов объема не меньше h3 (h - постоянная Планка).
В квантовой статистике элементарный объем шестимерного фазового пространства (элементарная ячейка) DГV = h3, а элемент трехмерного пространства импульсов
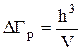 , (38)
, (38)
где V - элементарный объем для свободной частицы, т. е. фазовое пространство квантуется.
Найдем число состояний частицы из интервала энергий (W, W + dW).
Для этого проведем в пространстве импульсов две сферические поверхности с радиусами р и р + dp (рис. 9).
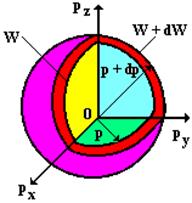 Рис. 9
Рис. 9
|
Шаровой слой имеет объем
V = 4p p2dp.
Число элементарных ячеек в этом слое
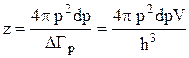 . (39)
. (39)
Поскольку каждой фазовой ячейке отвечает одно состояние микрочастицы, то число состояний, приходящихся на интервал dp, заключенный между р и p + dp, т. е.
g(p) dp = z.
Если свободные частицы не взаимодействуют друг с другом, то энергия частицы
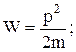
а ее изменение
 .
.
Тогда
р2 =2mW;
 .
.
Следовательно, число состояний
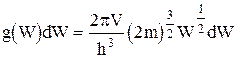 . (40)
. (40)
Таким образом, плотность состояний
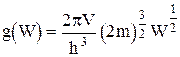 . (41)
. (41)
Замечание: Для электронов каждой фазовой ячейке соответствуют два состояния, отличающиеся друг от друга направлением спина, т. е. существуют спиновые состояния.
Следовательно, для электронов число состояний необходимо удвоить:
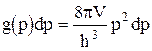 , (42)
, (42)
 . (43)
. (43)
Плотность состояний
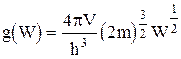 . (44)
. (44)
Если функцию распределения Ферми - Дирака
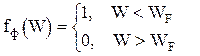
умножить на число состояний g(W)dW, то получим полную функцию распределения Ферми -Дирака при Т = 0 К
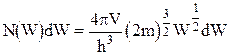 . (45)
. (45)
Так как в интервале энергий от 0 до WF функция распределения Ферми-Дирака fф = 1, то после интегрирования (5.82) в пределах от 0 до WF получим число частиц
 . (46)
. (46)
Учитывая, что n0 = N / V - концентрация электронного газа в металлах, получим формулу энергии Ферми:
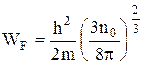 . (47)
. (47)
Зная функцию распределения электронов по энергиям можно найти среднюю энергию электрона при Т = 0 К:
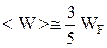 .
.
Максимальная скорость электронов на уровне Ферми
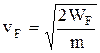
или vF » 106 м/c.
Средняя квадратичная скорость
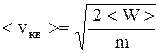 .
.
Дата добавления: 2016-02-09; просмотров: 2621;
