Вывод закона Видемана - Франца.

Основатели классической теории проводимости металлов пытались теоретически получить закон Видемана - Франца:

k / g = Const. (12)

При постоянной температуре для всех металлов отношение коэффициента теплопроводности к коэффициенту электропроводности является величиной постоянной.

Исследования Лоренца показали, что

k / g = L×T, (13)

где L - константа Лоренца.

Из молекулярно-кинетической теории известно, что коэффициент теплопроводности k = 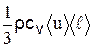, (14)

где с_v - удельная теплоемкость идеального газа при постоянном объеме;

r = mn₀ - плотность одноатомного газа.

Если молярная масса газа М = mN_a, то

r с_v = 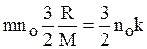, (15)

где R - универсальная газовая постоянная; k - постоянная Больцмана.

Следовательно,

k = 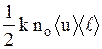. (16)

Подставив значение коэффициентов теплопроводности из (16) и электропроводности из (11) в (15), получим закон Видемана - Франца в виде k / g = k m<u>² / q²

Из молекулярно-кинетической теории следует, что <u> @<v_кв> = .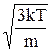

Тогда окончательно получим

k / g = 3k²T / q², (17)

где константа Лоренца L = .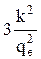

Несмотря на то, что классической теории удалось получить законы Ома и Джоуля-Ленца при выводе закона Видемана-Франца встретились серьезные трудности. Значение константы L значительно расходилось с экспериментальными данными.

Для металлов бериллия и марганца закон Видемана - Франца не выполняется.

Попытки Лоренца уточнить теорию, используя классическую статистику Максвелла-Больцмана, не дали результатов. Действительно, сильно упрощенная классическая теория проводимости металлов не могла учесть всех особенностей свойств электрона, которые были получены позднее.

Например, 1) согласно теории удельное сопротивление

~ ,

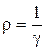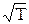что противоречит экспериментальным данным;

2) средняя длина свободного пробега электронов значительно больше и состаляла сотни периодов кристаллической решетки, т. е. электроны значительно реже испытывают столкновения с ионами;

3) более значительные затруднения теории возникли при объяснении теплоемкости металлов.

Молярная теплоемкость металлов определяется молярной теплоемкостью кристаллической решетки С_реш и молярной теплоемкостью электронного газа С_эл, т. е. С = С_реш + С_эл. Ионы, образующие кристаллическую решетку проводника, совершают тепловые колебания около узлов кристаллической решетки. Любой ион имеет три колебательные степени свободы и характеризуется в среднем энергией колебательного движения W_koл = 3 kT.

Тогда внутренняя энергия одного моля ионов U_реш = N_a 3kT = 3RT.

Следовательно, теплоемкость решетки (закон Дюлонга и Пти)

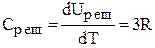. (18)

Теплоемкость электронного газа С_эл = 3R/2, (19)

Таким образом, полная теплоемкость металл

С_эл = 9R/2. (20)

Согласно экспериментальным данным молярная теплоемкость металлов почти не отличается от молярной теплоемкости кристаллических диэлектриков при нормальных условиях и находится по формуле С = 3R, т. е. электронный газ практически не имеет теплоемкости.

Трудности классической теории удалось преодолеть после создания качественно новой квантовой теории проводимости металлов, предложенной Зоммерфельдом в 1928 г. В своей теории он использовал статистику Ферми-Дирака. Согласно выводам квантовой теории константа L в законе Видемана-Франца L = 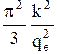, (21)

что хорошо согласуется с экспериментальными данными.

В квантовой теории учтено влияние периодического электрического поля на движение электронов, созданного ионами кристаллической решетки, нарушения этой периодичности за счет тепловых колебаний ионов, наличия примесей и т. д.