Распределение электронов в металлах. С повышением температуры металла электроны подвергаются тепловому возбуждению и переходят на более высокие энергетические уровни

по энергиям при Т ¹ 0 К.

С повышением температуры металла электроны подвергаются тепловому возбуждению и переходят на более высокие энергетические уровни. Однако в интервале температур при kT<< W_F не все электроны получают энергию.

Действительно, все состояния, кроме тех, что находятся в области энергии Ферми (в интервале шириной kT), заняты. Например, при Т = 300 К энергия электронов составляет 0,025 эВ. Поэтому число электронов, подвергнутых тепловому возбуждению, от общего их числа в металле составляет 1 %.

На рис. 5 приведен график зависимости функции распределения Ферми-Дирака (f = 1) от энергии электрона при Т ¹ 0 K, а на рис. 6 –график распределения электронов в металле по энергиям при Т ¹ 0 K.

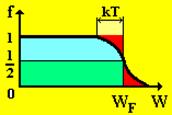Рис. 5

Средняя энергия электрона в металле при Т ¹ 0 K

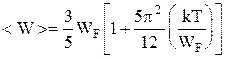. (28)

Так как при комнатной температуре kT << W_F, то

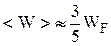. (29)

Вывод: Во всем диапазоне температур, в котором электронный газ является вырожденным, его распределение по энергиям мало отличается от распределения при Т = 0 К. Тепловому возбуждению подвергается незначительная часть электронов, находящихся близко к уровню Ферми.

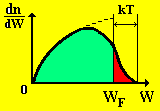Рис. 6

Концентрация и средняя скорость движения электронов не зависит от температуры. В квантовой механике доказывается, что с повышением

температуры значение энергии Ферми незначительно понижается и для металлов можно пренебречь этим изменением.

Замечание: Однако незначительное понижение энергии Ферми (химического потенциала m) при увеличении температуры имеет решающее значение для термоэлектрических явлений, особенно для полупроводников.

Строгий вывод закона Ома на основании квантовой теории является сложной задачей. Поэтому рассмотрим этот вопрос только качественно. Каждый электрон под действием электрического поля движется с упорядоченной скоростью. По квантовой теории закон Ома имеет вид j = gE, (30)

где (31)

– средняя длина свободного пробега электрона на уровне Ферми; u(F) – cредняя скорость электрона на уровне Ферми.

В квантовой теории проводимости металлов движение электронов в металлах рассматривается, как процесс распространения электронных волн де Бройля, которые рассеиваются при взаимодействии с ионами кристаллической решетки проводника. Рассеяние электронных волн и связанное с ним сопротивление проводников возникает, если в кристаллической решетке существуют центры рассеяния – различные искажения (дефекты) правильной структуры кристалла, для которых период кристаллической решетки d больше длины волны де Бройля электрона. Центрами рассеяния являются флуктуации плотности, возникающие в кристаллах в результате тепловых колебаний узлов решетки.

Таким образом, причинами появления электрического сопротивления твердых тел, в том числе и металлов, согласно квантовой теории являются различные искажения кристаллической решетки, вызывающие нарушение периодичности ее потенциала, на которых происходит рассеяние электронных волн и ослабление упорядоченного потока электронов.

Если сила сопротивления движению электронов будет равна силе, действующей со стороны, приложенного к проводнику электрического поля, то электроны будут совершать направленное движение с постоянной дрейфовой скоростью в направлении, противоположном вектору напряженности электрического поля, т. е. 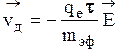, (32)

где m_'эф – эффективная масса электрона; t – время релаксации (для чистых металлов t » 10^-14 с – характеризует быстроту установления в системе равновесного состояния).

Отношение дрейфовой скорости к напряженности электрического поля называют подвижностью:

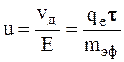. (33)

Для электронов u_n < 0. В СИ подвижность измеряют в м²/(B×c)