Классическая теория электропроводности металлов. На основании ряда экспериментальных данных, полученных учеными Рикке, Мандельштамом и Папалекси, Толменом и Стюартом в начале XX в
На основании ряда экспериментальных данных, полученных учеными Рикке, Мандельштамом и Папалекси, Толменом и Стюартом в начале XX в. было установлено, что носителями тока в металлах являются электроны.
Некоторые свойства электрона были описаны Томсоном в 1895-97 гг.
Большая концентрация электронов в металлах (no » 1028 - 1029 м-3) обуславливает в них высокую тепло- и электопроводимость. Позднее была создана классическая теория электропроводности металлов Друде-Лоренца.
В основу теории были положены выводы классической молекулярно-кинетической теории, в которой электроны проводимости рассматриваются как электронный газ и его свойства подобны свойствам одноатомного, идеального газа. Число свободных электронов равно примерно числу атомов.
Согласно классической электронной теории проводимости металлов в отсутствии электрического поля в них электроны проводимости (электронный газ) находятся в состоянии теплового хаотического движения в кристаллической решетке, образованной положительно заряженными ионами.
Ионы совершают тепловые колебания около положений равновесия - узлов кристаллической решетки. При своем движении электроны испытывают столкновения с ионами. Длина свободного пробега электронов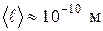 
, т. е. по порядку равна периоду кристаллической решетки. В соответствии с выводами молекулярно-кинетической теории средняя кинетическая энергия теплового движения электронов 
,
где m - масса электрона; <vкв> - средняя квадратичная скорость теплового движения. Например, при температуре Т = 273 К, <vкв> » 105 м/c.
При создании электрического поля в металлических проводниках возникает электрический ток, плотность которого
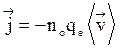, (1)
где n0 - концентрация электронов; qe - заряд электрона; <v> - средняя скорость упорядоченного движения. Электроны имеют скорость v = <u> + <v>.
Следовательно, под действием напряженности электрического поля электроны в проводнике приходят в упорядоченное движение в направлении противоположном вектору напряженности электрического поля.
При максимально допустимой плотности тока в металлах cредняя скорость упорядоченного движения <v> » 10-3 м/c, т. е. <v> << <u>, что объясняется малым значением средней длины свободного пробега электрона между двумя последовательными столкновениями его с ионами.
Вывод закона Ома
По классической теории проводимости металлов при соударении электрона с ионом он полностью теряет свою скорость.
Уравнение движения электрона в электрическом поле в процессе свободного пробега является равноускоренным.
Поэтому на основании второго закона Ньютона
F = ma = m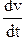 
,
где F = qeE; Е - напряженность электрического поля.
Средняя скорость упорядоченного движения
<v> = 
.
Если средняя продолжительность времени свободного пробега <t>, то после интегрирования
F = ma = m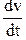 
получим, что <vмах> = 
или
<v> =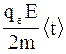 
. (2)
Если <u> всех электронов одинаковы, но <v> << <u>, найдем среднее время пробега электрона
.
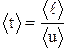С учетом этого формулу (2) перепишем в виде:
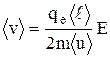. (3)
Следовательно, плотность тока
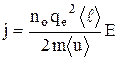, (4)
где 
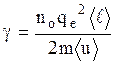(5)
- удельная электропроводимость проводника.
Таким образом, на основании классической теории проводимости металлов был теоретически получен закон Ома в дифференциальной форме
j = g E.
Дата добавления: 2016-02-09; просмотров: 692;