Термодинамика процесса. Рассмотрим закрытую систему при температуре T и давлении P, в которую поместили nMeO молей оксида металла MeO

Рассмотрим закрытую систему при температуре T и давлении P, в которую поместили n_MeO молей оксида металла MeO, и n_C молей твердого углерода. Требуется определить выход и состав фаз. Такую задачу можно решать в самом общем виде, применяя компьютерные методы. Мы рассмотрим возможность частного решения для случая, когда предполагаем, какие фазы сосуществуют в равновесии.

Допустим, в равновесии будут сосуществовать металл, оксид, твердый углерод и газ. Тогда задача сводится к нахождению пяти неизвестных в равновесии: x_Me, x_MeO, x_C, x_CO, x_CO2. Допустим, заданы температура и давление (как и раньше для закрытой системы задаем два экстенсивных параметра, т.е. предполагая, что в системе две степени свободы) и исходный элементный состав системы: n_MeO, n_Me и n_C. Составим необходимые пять уравнений:

Баланс по кислороду:

n_MeO= x_CO + 2∙x_CO2 + x_MeO

Баланс по металлу

n_Me = x_Me + x_MeO

Баланс по углероду:

n_C = x_C + x_CO + x_CO2

Константа реакции MeO + CO = Me + CO₂:

K_p1 = x_CO2/x_CO

Константа реакции Будуара: C + CO₂ =2CO

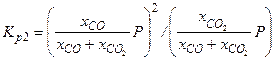
Решая эту систему можно определить все пять неизвестных. Проанализируем последние два уравнения. Эти уравнения образуют так называемую замкнутую подсистему, т.е. они связывают только два неизвестных x_CO и x_CO2, и состав газовой фазы не зависит от того, сколько молей C и MeO мы загрузили в систему - эти величины участвуют лишь в первых трех уравнениях. Решая последние два уравнения, мы приходим к решению x_CO=0, что естественно вызывает недоумение. Учитывая, что математические выкладки выполнены правильно, значит ошибка была в постановке задачи. При произвольно выбранных P и T в равновесии в данной закрытой системе не могут сосуществовать четыре фазы.

Этот результат обусловлен тем, что мы предварительно не провели анализ с использованием правила фаз (ПФГ) Гиббса. Согласно ПФГ в нашей системе 3 компонента и 4 фазы. В этом случае число степеней свободы равно 1 и мы можем произвольно задать только один внешний параметр (T или P), а второй будет зависимым. В изобарно-изотермической системе, в которой T и P задаются, т.е. заранее используются две степени свободы согласно правилу фаз (Ф=К+2-С) максимальное число фаз в равновесии должно быть равно числу компонентов т.е. трем - две конденсированные фазы и газ. Т.е. в рассматриваемой системе возможны следующие равновесия:

а) Me+MeO в случае, если углерода было мало, а температура достаточна для протекания реакции восстановления. В этом случае весь C расходуется (недостаток углерода). Термодинамический анализ аналогичен проведенному ранее для случая восстановления оксида газообразными восстановителями CO-CO₂.

б) MeO+C в случае, если реакция восстановления практически не пошла. Это может быть только в том случае, если исходно в системе не было чистого металла (n_Me=0), в равновесии x_Me=0. Равновесный состав газовой фазы определяется реакцией Будуара. При этом (x_CO + x_CO2)-->0. (Без предположения о существовании области гомогенности у MeO этот вариант не объясним).

в) Me+C в случае, если реакция прошла, оксид полностью восстановился до металла, но углерод весь не израсходовался (избыток углерода). Равновесный состав газовой фазы также определяется реакцией Будуара.

И, наконец, необходимо указать, при каких условиях реализуются эти равновесия. Особенно наглядно это можно показать графически. Будем считать, что общее давление равно одной атмосфере и нанесем на график зависимости C_CO от T, полученные из уравнений восстановления металла CO и уравнения Будуара (если в системе остался твердый углерод).

При постоянном (в данном случае атмосферном) давлении эти две кривые пересекаются в одной точке, значит одновременно сосуществовать в равновесии Me, MeO, C и газ могут лишь при одной единственной температуре. Если кривая для оксида идет выше кривой Будуара восстановления не происходит, если ниже в системе образуется металл (если конечно в системе достаточно углерода для полного восстановления. Сказанное можно проиллюстрировать диаграммой на рисунке 4.17.