Кинетикой химических реакций называется учение о скоростях реакций

В кинетике рассматриваются факторы, определяющие скорости реакций, а также промежуточные состояния, при помощи которых достигается конечный результат. Кинетика химических реакций приобрела более общее значение, так как ее законы оказались применимы для многих других процессов вплоть до ядерных реакций и процессов, протекающих в недрах звезд и в живых организмах.

Химическая кинетика изучает реакции и процессы в их движении, в отличии от термодинамики, которая ограничивается лишь рассмотрением статики химических реакций — равновесий. Термодинамика при наличии некоторых исходных данных может предсказывать эти равновесные состояния. Однако между величиной изменения энергии Гиббса при реакции и ее скоростью не существует прямой связи Так, реакция образования воды из H₂ и O₂ идет с меньшей скоростью, чем реакция между ионами‚ H⁺ и ОН^-, хотя первая сопровождается значительно большей убылью энергии Гиббса. Таким образом, вопросы о том, в течение какого времени и каким путем совершаются те или иные процессы, находятся вне рамок термодинамики. Время вообще не входит в термодинамические уравнения.

Между тем потребности практики требуют знания закономерностей, определяющих протекание химических процессов во времени. Это необходимо для разработки методов интенсификации процессов в промышленных агрегатах, а также способов их автоматизации. Так, установление временного закона, описывающего протекание реакции обезуглероживания стали, необходимо для создания автоматического управления конвертерами и открывает возможность оптимизации их работы.

Химическая кинетика имеет большое научное значение, так как она дает наиболее общие методы выяснения механизма реакций. Знание кинетических характеристик реакций и процессов необходимо для расчета аппаратуры металлургической промышленности.

В зависимости от того, протекают ли реакции (процессы) в гомогенной среде или в гетерогенной, они, соответственно, подразделяются на гомогенные или гетерогенные. Металлургические процессы как правило сложные многоэтапные (многоступенчатые), протекающие через несколько стадий физико-химических взаимодействий (диффузионный и конвективный массоперенос внутри фаз, массопередача на границах раздела фаз, химические реакции в объеме и на поверхностях раздела фаз, процессы адсорбции и десорбции и т.д.), каждая из которых описывается своими кинетическими закономерностями. С определенной точки зрения теоретическое описание динамики металлургического процесса зачастую оказывается существенно сложнее описания его термодинамики, очевидно, поэтому в настоящее время при исследовании динамики металлургических процессов, т.е. скорости и механизмов перехода из исходного в равновесное состояние, гораздо чаще, чем при термодинамических исследованиях, прибегают к экспериментальным методам.

Цель анализа и моделирования динамики процессов состоит в предсказании поведения процесса во времени. Если при моделировании равновесия мы стремимся предсказать конечное, равновесное, состояние, к которому стремится система, то при моделировании динамики задачей является предсказание того, как изменяются во времени параметры при стремлении к равновесию. Поэтому логичным будет при исследовании конкретного металлургического процесса провести сначала термодинамическое (равновесное) моделирование и убедиться в том, что прогнозируемые результаты, т.е. то состояние, к которому стремится система, удовлетворяют нас с металлургической точки зрения. Только после этого рекомендуется приступать к анализу динамики поведения параметров процесса, т.е. того, как быстро система переходит в это состояние.

Моделирование динамики имеет еще одно существенное отличие от моделирования равновесия. При анализе динамики построении динамических моделей практически невозможно обойтись без экспериментального этапа. Это объясняется тем, что при переходе системы из начального состояния в равновесное она испытывает так называемые динамические торможения, или кинетическое лимитирование. Выяснить природу этого лимитирования и определить его параметры обычно возможно только экспериментально. Это объясняется тем, что факторов, влияющих на скорость процесса очень много. Так, окисление металла может зависеть не только от термохимических параметров - концентрации окислителя и температуры, но и от формы детали, степени ее механической обработки, скорости и метода подачи окислителя, геометрической конфигурации реактора и самой детали и т.д. В этой связи становится понятным, почему, в отличии от термодинамики, не существует каких-либо справочников параметров динамики или кинетики.

Еще одно отличие динамических моделей от равновесных - это тип уравнений, применяемых для описания поведения процессов. Учитывая, что цель моделирования динамики - предсказание поведения параметров системы во времени, становится понятным, почему математический аппарат при моделировании динамики представлен обыкновенными дифференциальными уравнениями.

Как известно из курса физической химии скоростью химической реакции w называется скорость изменения концентрации какого-либо из участвующих в ней веществ. В гетерогенных реакциях, протекающих на поверхности пористых твердых тел, скорость реакции относят к единице массы или объема твердой фазы, а в случае жидких или твердых фаз при известной поверхности - к единице поверхности раздела. Величина w имеет отрицательный или положительный знак в зависимости от того, исчезает или образуется вещество в ходе данной реакции. Для реакции аА+bВ→gG+hH скорость может выражаться одной из следующих производных;

-dC_A/dτ, -dC_B/dτ, +dC_G/dτ, +dC_H/dτ

где: τ - время; С_А, С_B, С_G и С_H - концентрации.

Величины этих производных связаны между собой стехиометрическими коэффициентами a,b,g,h. В общем случае, скорость химической реакции является функцией многих переменных (концентрации, температуры, давления и др.) w=f(T,C_i,P..).

Скоростью изменения концентрации компонента можно характеризовать не только скорость отдельной химической реакции, но и сложного многостадийного физико-химического процесса, которые, как правило, протекают в металлургическом аппарате. При этом, скорость всего процесса определяется скоростью наиболее медленной стадии, которая называется лимитирующей. Увеличение скорости протекания наиболее медленной стадии процесса позволяет наиболее эффективно интенсифицировать процесс в целом. Учитывая это, становится понятным, почему кинетические исследования металлургических процессов часто направлены, прежде всего, на определение лимитирующей стадии динамики металлургического процесса.

Для того, чтобы продемонстрировать основные подходы к исследованию (моделированию) динамики металлургических процессов будем использовать следующий пример.

Пример. В реактор загружен 1 кг латуни, рисунок 5.1. Сплав нагрет до температуры 1400 К. Воздух из системы откачан и в системе поддерживается практически вакуум с остаточным давлением 1 Па. Требуется предсказать поведение параметров системы во времени.

Для анализа динамики процесс необходимо провести выбор описываемых параметров. В начале выбираются целевые параметры, затем, после записи уравнений - вспомогательные.

Пример. В качестве целевых параметров рассматриваемой задачи выбраны - масса сплава в реакторе, масса цинка в сплаве и масса меди в сплаве. Следовательно, требуется построить систему дифференциальных уравнений типа:

()

()

()

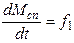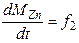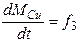На втором этапе требуется понять, какова будет структура системы дифференциальных уравнений. Это значит, что необходимо выяснить, от каких параметров зависят функции fi, каков вид этих зависимостей, какие еще уравнения для вспомогательных параметров необходимо записать, чтобы система имела решение.

Анализа динамики химических процессов в большинстве случаев проводится на основе экспериментальных данных, в процессе которых, прежде всего, тем или иным способом производится регистрация скорости протекания химического процесса. Рассмотрим основные, наиболее часто используемые методы регистрации скорости процессов в пирометаллургии.

Методы регистрации скорости в пирометаллургии

В теории пирометаллургических процессов существует несколько традиционных способов регистрации динамики процессов. Одна часть этих способов позволяет проводить непрерывную регистрацию параметров, связанных со скоростью протекания процессов. Другая - требует постановки нескольких экспериментов с разным временем проведения процессов. Существует и традиционное оборудование для этих целей. Разумеется, методика проведения динамического эксперимента и его аппаратурное оформление постоянно модифицируются и совершенствуются. Имеются специальные монографии, посвященные технике металлургического эксперимента . Остановимся лишь на наиболее распространенных, ставших уже стандартными методиках.

Дифференциальная гравиметрия. Метод основан на непрерывном измерении изменения массы образца с помощью специальных высокотемпературных весов, рисунок 5.2. Отметим, что этот метод позволяет фиксировать лишь общее изменение массы. В англоязычной литературе метод получил сокращенное название DTG (Differential Thermic Gravimetry). Имеется ряд серийно выпускаемых приборов для этого метода. Например, установки типа ДРОН и SETARAM.

Дифференциальнотермический анализ. Метод применяют для процессов со значительным выделением или поглощением тепла. Непрерывно регистрируется тепло, выделяемое в ходе процесса, которое связано с массой прореагировавшего вещества, рисунок 5.3. Установка обычно включает в себя две термопары, одна из которых показывает температуру печи, другая - температуру в зоне процесса. Сигнал первой термопары вычитается из сигнала второй. Таким образом фиксируется "чистое" тепло процесса.

Хроматографический анализ. Метод применяют для процессов со значительным выделением газообразных продуктов реакции. Газ выходящий из реактора полунепрерывно анализируется на хроматографе - приборе позволяющем проводить разделение газа на отдельные вещества и определять их количества, рисунок 5.4. Существует большое разнообразие хроматографов различных фирм.

Метод отбора проб. Из реактора периодически отбирается проба вещества и анализируется ее состав. При использовании этого метода необходимо стремиться, чтобы величина пробы была бы не слишком большой. В противном случае это может существенным образом сказаться на протекании процесса в оставшееся время.

Пример. Для рассматриваемого процесса испарения латуни не ожидается большого тепловыделения и теплопоглащения, следовательно метод дифференциальнотермического анализа - малопригоден. В хроматографах газовая смесь, выходящая из реакционной зоны охлаждается, что может привести к конденсации паров и порче прибора, поэтому этот метод также непригоден для регистрации кинетики процесса испарения. В дифференциальной гравиметрии используют особо точные аналитические весы. В нашем же плане эксперименты с перемешиванием расплава. Такое перемешивание, разумеется, нельзя проводить в реакторе, помещенном на аналитические весы. Поэтому из всех стандартных методов можно использовать метод отбора проб.

В реактор загружается навеска вещества. Реактор откачивается до заданного давления и нагревается до заданной температуры. После выдержки в течении определенного времени, например 5 минут, реактор необходимо быстро вынуть из печи и быстро охладить. После этого взвешивается на обычных аналитических весах масса сплава, берется проба на химический анализ. После этого всю процедуру придется повторить для времени выдержки 10 минут, 15 минут и т.д. Можно сразу завесить в печь несколько реакторов и вынимать их из зоны высоких температур через разные интервалы времени. Выбор конкретного плана эксперимента часто зависит от привычки экспериментатора и возможностей аппаратуры.

После выбора методик эксперимента проводится собственно эксперимент, результатом которого являются зависимости тех или иных параметров от времени (например, масса прореагировавшего вещества от времени). Эти зависимости называются кинетическими кривыми. Анализ кинетических кривых позволяет определить параметры кинетики (динамики) процесса - энергии активации, предэкспоненциального множителя, порядка реакции, лимитирующие стадии и т.п.

Рассматривая методы регистрации динамики процессов, мы убедились, что в каждом из них контролируется свои параметры. Для моделирования же динамики процессов требуется привести их к какой-либо единой системе координат. Сами параметры, фиксируемые тем или иным методом регистрации динамики процесса можно разделить на два класса.

К первому отнесем параметры, связанные с изменением состояния системы в данный момент времени. Такие параметры называют дифференциальными. К дифференциальным параметрам, например, относится тепло, выделяемое в процессе и регистрируемое дифференциальнотермическим методом, а также состав газовой фазы, регистрируемый хроматографическим методом.

Ко второму классу относятся параметры, характеризующие изменения состояния системы от начала процесса к данному моменту времени. Такие параметры называют интегральными. К ним относятся, например, изменение общей массы в реакторе, регистрируемое гравиметрическим методом и методом отбора проб.

В разных экспериментах возможно измерение совершенно различных параметров, однако в кинетике вводится понятие безразмерной степени протекания процесса, интегрального параметра.

Определение. Степенью протекания процесса называют отношение количества вещества, принявшего участие в процессе к данному моменту времени, к общему количеству вещества, способному прореагировать в процессе при достижении состояния равновесия. Степень протекания выражается в долях единицы или в процентах.

Для определения степени протекания необходимо знать равновесное количество вещества, и его количество, прореагировавшего к данному моменту времени.

Пример. Если в исходной навеске латуни содержалось 0,1 кг сплава, то масса цинка в начальный момент времени была равна 0,02 кг. В равновесной открытой системе цинка и меди в реакторе не останется, т.к. газовая фаза постоянно откачивается из него. Если в результате эксперимента установлено, например, что через 20 минут масса цинка в реакторе стала составлять 0,015 кг, то степень протекания процесса удаления цинка к 20-ой минуте составила:

(M_ИСХ-М₂₀)/(М_ИСХ-М_РАВН) = (0,02-0,015)/(0,02-0,00) = 0,250 или 25%

Введя безразмерный параметр, степень протекания процесса, мы можем сравнивать динамику поведения процессов в огромной действующей печи и маленьком лабораторном реакторе.

Аналогично интегральному параметру - степени протекания вводится и безразмерная скорость процесса.

Определение. Безразмерной скоростью процесса называют скорость изменения степени протекания.

Два введенных параметра связаны друг с другом естественными соотношениями:

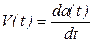
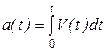
Данные формулы могут служить теоретической базой для обоснования связи интегральных и дифференциальных динамических функций. Однако на практике приходится иметь дело не с аналитическими функциями, а с табличными или графическими зависимостями. Поэтому требуются формулы для пересчета степени протекания по скорости процесса и обратно, применимые в этих прикладных ситуациях. Такие формулы выводятся в курсе Прикладной математики и здесь мы напомним их без вывода.

Для расчета степени протекания по известной скорости процесса можно использовать метод трапеций или метод Симпсона. Для этого весь интервал времени разбивается на n частей. На практике n обычно изменяется в пределах от 10 до 20. В каждый из моментов времени выписывается значение скорости vi. Тогда степень протекания в i-ый момент времени равна по формуле трапеций:

Для расчета скорости процесса по известной степени протекания необходимо использовать формулы численного дифференцирования. К сожалению, задача численного дифференцирования относится к классу так называемых некорректных задач, поэтому формулы численного дифференцирования нужно использовать с большой осторожностью. Простейшая формула для численного дифференцирования выглядит так:

Результаты эксперимента при температуре 1000 К

Время, сек Zn, %(масс) Cu, %(масс) Масса сплава,г

0 19,98 80,00 99,98036
60 19,04 80,93 98,83046
120 18,14 81,83 97,73469
180 17,26 82,72 96,69168
240 16,40 83,58 95,69994
300 15,57 84,41 94,75791
360 14,76 85,21 93,86404
420 13,99 85,99 93,01668
480 13,24 86,74 92,21426
540 12,52 87,46 91,45512
600 11,83 88,15 90,73758

Результаты эксперимента при температуре 1200 К

Время, сек Zn, %(масс) Cu, %(масс) Масса сплава, г

0 19,87 80,00 99,87
60 14,45 85,45 93,53
120 10,10 89,83 89,00
180 6,846 93,11 85,88
240 4,526 95,45 83,79
300 2,941 97,05 82,42
360 1,888 98,11 81,53
420 1,203 98,80 80,97
480 0,762 99,23 80,61
540 0,481 99,52 80,38
600 0,303 99,70 80,24

Рассчитав массы металлов, оставшихся в сплаве и степень протекания процесса испарения цинка получили:

Расчеты для эксперимента при температуре 1000 К

Время, сек МZn, гр МCu, гр Степень протекания

0 20,00 80 0,000
60 18,83 80 5,847
120 17,73 80 11,32
180 16,69 80 16,54
240 15,70 80 21,49
300 14,75 80 26,20
360 13,86 80 30,67
420 13,01 80 34,91
480 12,21 80 38,92
540 11,45 80 42,72
600 10,73 80 46,31

Расчеты для эксперимента при температуре 1200 К

Время, сек МZn, гр МCu, гр Степень протекания

0 19,87 80 0,000
60 13,53 80 32,34
120 9,000 80 54,99
180 5,880 80 70,59
240 3,792 80 81,03
300 2,423 80 87,88
360 1,538 80 92,30
420 0,972 80 95,13
480 0,613 80 96,93
540 0,385 80 98,07
600 0,242 80 98,78

Графически изменения степени протекания процесса испарения цинка даны на рисунке 5.5.

Для определения кинетических параметров по кинетическим кривым необходимо определиться в рамках какой кинетической модели описывается данный процесс.

Дело в том, что металлургические процессы весьма разнообразны по механизму и условиям протекания. Наиболее простой случай – протекание физико-химических взаимодействий в гомогенной однофазной системе. Уравнения для описания кинетики реакций в гомогенных системах наиболее просты (см. выше и курс физической химии), однако, в подавляющем числе случаев металлургические процессы протекают в гетерогенных системах. Описание механизма и динамики таких процессов гораздо сложнее и включает несколько стадий взаимодействий, описываемых различными законами и уравнениями – молекулярная диффузия в газовых и конденсированных средах, конвективных массоперенос в газовых и жидких средах, процессы адсорбции и десорбции, химические реакции и т.д. В этом случае суммарная скорость всего процесса определяется самой медленной (или лимитирующей) стадией и зачастую вид кинетической кривой всего процесса аналогичен виду кривой, описывающей лимитирующую стадию. Таким образом, для анализа металлургического процесса важнейшим является определение лимитирующей стадии и ее кинетических параметров, на основании чего можно определить меры по ускорению как наиболее медленной стадии, так и всего процесса в целом.

Стадии, периоды и механизмы процессов. Выявление лимитирующего фактора протекания физико-химических процессов. Особенности кинетики процессов диссоциации, окисления и восстановления

Типы динамического лимитирования (лимитирующих стадий).

При моделировании динамики различают несколько основных типов функций f в зависимости от того, какова природа кинетического торможения (лимитирующей стадии). Наиболее часто в кинетике гетерогенных процессов, т.е. процессов, происходящих на поверхностях раздела, лимитирующими бывают химические реакции, внутренняя и внешняя диффузия и физическая адсорбция. В общем виде уравнения, описывающие скорость процессов для этих трех случаев следующие:

а) Лимитирует скорость химической реакции (кинетический вариант закона Гульдберга и Вааге:

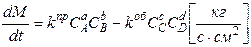
где: k^при k^об- константы скорости прямой и обратной реакции; СIi- концентрации веществ в соответствующих степенях;

Иногда вместо концентраций используют активности, для газообразных веществ - давления. Показатели степени называют порядком реакции по веществу. Для некоторых процессов имеет значение только скорость прямой реакции. В этом случае второй член в уравнении отсутствует. Константы скорости реакций зависят от температуры (закон Аррениуса):

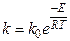
где k_o - предэкспоненциальный множитель, Е - энергия активации реакции, измеряемая в единицах энергии. Ее значение обычно изменяется от 30 до 80 кДж/моль.

б) Лимитирует внутренняя диффузия (первый закон Фика):

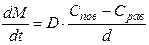
где: D - коэффициент диффузии, Спови Срав- концентрация вещества на поверхности и равновесная (в объеме фазы) концентрации, d - толщина слоя, через который происходит диффузия.

Также, как и при кинетическом лимитировании, для газообразных веществ вместо концентраций могут быть использованы давления. Для сферических частиц, если толщина диффузионного слоя достаточно велика по сравнению с радиусом самой частицы используют несколько более сложную форму уравнения. Коэффициент диффузии зависит от температуры точно таким же образом, как и константа скорости химической реакции (закон Аррениуса):

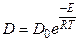
где Do- предэкспоненциальный множитель, Е - энергия активации внутренней диффузии, ее значение обычно изменяется от 5 до 20 кДж/моль, т.е. она в меньшей степени зависит от температуры, чем скорость химической реакции.

в) Лимитирует внешняя диффузия:

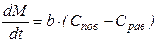
где b - коэффициент внешней массопередачи, зависящий от интенсивности перемешивания газообразной или жидкой фазы.

г) Лимитировать скорость процессов могут и некоторые другие явления. В этом случае в литературе можно найти соответствующие уравнения. Так при кристаллизации лимитирующим может быть процесс образования новой фазы, при адсорбции - наличие на поверхности частиц свободного места и т.п.

Методы определения лимитирующих стадий

Для того, чтобы установить, какое именно лимитирование характерно для конкретной системы, требуется провести специальный кинетический эксперимент. Логика планирования подобного эксперимента состоит в следующем. Как видно из приведенных выше уравнений, на скорость процесса при наличии разных типов лимитирующих стадий влияют разные параметры. Так изменение интенсивности внешнего перемешивания газообразной или жидкой фазы относительно частиц может существенно повлиять на скорость реакции только в том случае, если лимитирующая стадия - внешняя диффузия; повышение температуры наиболее существенно отразится на скорости процесса, если он тормозится химической реакцией; размер частиц наиболее существенно влияет на скорость процесса, если он лимитируется внутренней диффузией, т.к. от этого зависит толщина диффузионного слоя. Поэтому для определения лимитирующей стадии проводят несколько экспериментов, в которых задают различные внешние параметры. В зависимости от того, какие из параметров существенно повлияли на скорость процесса, делают вывод о типе лимитирующей стадии.

Действительно, в самом общем виде гетерогенный металлургический процесс состоит из следующих последовательно протекающих стадий, рисунок _:

1) Подвод реагента из объема к поверхности частицы (внешняя диффузия);

2) Адсорбция реагента на поверхности частицы;

3) Проникновение реагента сквозь слой продуктов (внутренняя диффузия);

4) Химическая реакция, которая в свою очередь может состоять из нескольких последовательных реакций;

5) Отвод продуктов реакции сквозь слой на поверхность частицы (внутренняя диффузия);

6) Десорбция продуктов с поверхности частицы;

7) Отвод продуктов в объем реактора (внешняя диффузия).

Разумеется, что для конкретного процесса какие-либо из перечисленных стадий могут отсутствовать.

Пример. В рассматриваемом процессе испарения металлов из латуни, естественно отсутствуют стадии 1, 2 и 3, так как никаких реагентов к поверхности расплава не подводится, а также стадия 5, потому что конденсированных продуктов на поверхности сплава не образуется. Таким образом, процесс состоит из следующих последовательных стадий:

1) Химические реакции, испарения цинка и меди;

2) Десорбция газообразного цинка и меди с поверхности сплава;

3) Отвод газа в объем реактора.

Проводя процесс, мы можем регистрировать каким-либо методом суммарную скорость процесса. Однако в теории массопередачи доказано, что, если процесс состоит из ряда последовательных стадий, то суммарная скорость процесса примерно равна скорости самой медленной, лимитирующей, стадии. Следовательно, регистрируя суммарную скорость процесса и влияние на нее различных параметров, мы по существу наблюдаем лишь одну, самую медленную стадию.

Для того, чтобы понять, какая именно стадия определяет скорость всего процесса мы должны провести логический анализ.

Пример. В рассматриваемом процессе увеличение мощности откачки газообразных веществ из реактора может повлиять на стадию 3. Увеличение температуры приведет к росту скорости стадий 1 и 2 и не повлияет на стадию 3. Перемешивание расплава и обновление межфазной границы приведет к росту скорости 2-ой стадии и не скажется на скоростях 1-ой и 3-ей стадий.

Такой анализ показывает, какие эксперименты требуется провести, чтобы установить лимитирующую стадию.

Пример. Из проведенного выше логического анализа видно, что можно провести два эксперимента с различными температурами расплава и без его перемешивания и один эксперимент с перемешиванием. Если в первых двух экспериментах скорость будет одинаковой, следовательно лимитирующей является внешняя диффузия, если разной - вторая или третья стадия. Если при перемешивании расплава скорость процесса испарения увеличится, следовательно лимитирующая стадия - десорбция, если останется без изменения - химическая реакция испарения.

Итак, после определения, какая из стадий является лимитирующей, можно разработать полную систему обыкновенных дифференциальных уравнений. Этот этап начинается с записи основного уравнения и его конкретизации.

Пример. Для анализируемого процесса основное уравнение, вытекающее из теории имеет вид:

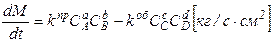
1. Для того, чтобы конкретизировать это уравнение необходимо условится, масса какого вещества стоит в правой части.

Пример. Из постановки задачи следует, что таких уравнений должно быть два: одно для цинка, другое - для меди. Но такие уравнения можно записать как для массы этих металлов в сплаве, так и для массы этих же металлов в газе. Первые массы будут уменьшаться, вторые - увеличиваться. Учитывая, что нами избран метод отбора проб сплава, логичным будет записать уравнения для изменения масс металла в сплаве. Тогда перед правой частью уравнения должен стоять знак минус.

2. Необходимо записать основные реакции и определить: какие вещества участвуют в процессе.

Пример. Реакции, протекающие при испарении металлов таковы:

Zn^P => Zn^Г;

Cu^P => Cu^Г.

Следовательно, основные уравнения будут выглядеть так:

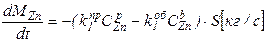
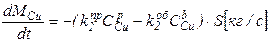
3. Определяем, какие параметры в основных уравнениях зависят от времени, а какие являются постоянными.

Пример. Очевидно из схемы проведения процесса, что площадь жидкость-газ не изменяется в течение всего процесса, следовательно S - величина постоянная. Константы скоростей реакций k - зависят лишь от температуры и не изменяются со временем, значит для них нужно записать лишь обычные, не дифференциальные, уравнения. Концентрации металлов в расплаве изменяются по ходу процесса, значит CZnри CCuр- являются функциями от времени и для них необходимо записать дифференциальные уравнения. Концентрации металла в газе практически равны нулю, так как в ходе процесса происходит постоянная откачка газа из системы и внешняя диффузия не лимитирует, поэтому записанные уравнения можно упростить:

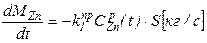
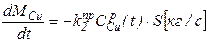
Итак, для того, чтобы система уравнений была бы полной, требуется записать два дополнительных дифференциальных уравнения для функций C_Zn^P (t) и C_Cu^P(t), а также два алгебраических уравнения для kпр1и kпр2. Учитывая, что нас также интересует и изменение общей массы сплава в реакторе запишем также и уравнение для Mсп.

4. Записываем полную систему уравнений.

Пример. Концентрация металлов в сплаве связана с их массой так:

C_Zn^P = M_Zn / (M_Zn +M_Cu);

C_Cu^P = M_Cu / (M_Zn +M_Cu).

Дифференцируя каждое из уравнений по времени, получаем:

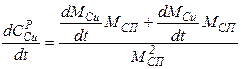
Для массы сплава:

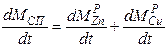
Для констант скорости реакций:

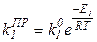
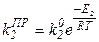
Итак, мы построили полную систему обыкновенных дифференциальных уравнений, представляющих собой модель динамики рассматриваемого процесса. Система состоит из пяти неизвестных функций:

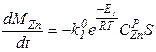
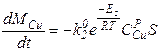
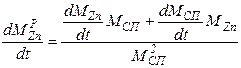
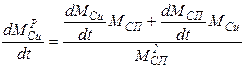
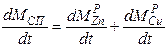
Для того, чтобы использовать полученную модель динамики для предсказания поведения системы, требуется определить, или, как говорят математики, идентифицировать, кинетические параметры. Для этого требуется поставить серию экспериментов и обработать их результаты.

Пример. Кинетическими параметрами построенной модели являются лишь коэффициенты в уравнении Аррениуса. Поэтому для их идентификации требуется провести серию экспериментов при различных температурах.

Допустим мы провели эти эксперименты для рассматриваемого случая (см. выше). Анализ позволяет несколько упростить уравнения

Как показывают результаты расчетов, медь испаряется практически очень медленно при температурах эксперимента, поэтому, во-первых, составленную систему уравнений можно упростить, приравняв dMCu/dt = 0. Тогда упрощенная система будет выглядеть так:

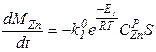
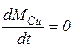
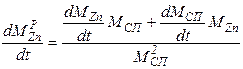
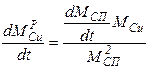
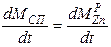
Во-вторых, в упрощенной системе осталось всего два кинетических коэффициента, которые требуется идентифицировать - ko1и E1.

Анализ уравнений () показывает, что в кинетике гетерогенных пирометаллургических процессов существует ряд стандартныхкинетических параметров. Конечно, некоторые процессы могут описываться и другими типами уравнений, однако примерно 95% всех процессов можно проанализировать, используя общие закономерности. В этой связи разработаны и стандартные процедуры нахождения, или идентификации, кинетических коэффициентов по экспериментальным данным о динамике процессов. Все эти процедуры можно разбить на три группы: графические, аналитические и компьютерные.

Графические процедуры предполагают построение графиков в таких координатах, где кинетические кривые трансформируются в прямые линии. Определяются параметры этих прямых и производится пересчет их в кинетические параметры.

Аналитические процедуры требуют каким-либо образом преобразовать дифференциальные уравнения динамики процесса в алгебраические уравнения. После чего находятся корни системы уравнений, которые и являются определяемыми кинетическими параметрами.

Компьютерные процедуры стали распространяться в последнее время в связи с широким распространением персональных компьютеров. Их суть заключается в том, что записывается система дифференциальных уравнений динамики, в которой можно изменять неизвестные кинетические коэффициенты. Система решается на компьютере несколько раз с разными значениями кинетических параметров. Выбираются значения тех параметров, при которых расчетные и экспериментальные кривые совпадают в наибольшей степени.

Пример. Рассмотрим каждую из процедур идентификации коэффициентов ko1и E1на примере описанного выше процесса.

Графическая процедура. Анализ основного уравнения динамики показывает, что, если площадь испарения S и концентрация цинка в сплаве CZnрравны для нескольких экспериментов с разными температурами, то зависимость скорости процесса от температуры выразится так:

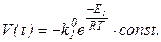
Если прологарифмировать это уравнение, то получим:

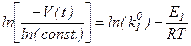
Если построить график в координатах ln[-v(t)/ln(const)] - 1/Т, то мы должны получить прямую линию

y =a+bx

где у = ln[-v(t)/ln(const)];

x = 1/Т;

a = ln(ko1);

b = -E1/R.

Определив по графику величины a и b, можно рассчитать и неизвестные кинетические параметры. Здесь необходимо отметить следующее. Как мы видели выше, для того, чтобы этот метод давал верные результаты, требуется, чтобы скорости процесса рассчитывались для всех экспериментов тогда, когда концентрация цинка в сплаве одинакова. Часто допускается ошибка и скорости определяются для одного и того же момента времени. В общем случае можно утверждать, что скорости должны определяться для разных моментов времени, когда равны (или примерно равны) степени протекания.

В нашем случае можно рассчитать скорость процесса для первого эксперимента на 360 секунде (а=30,67), а для второго эксперимента на 60 секунде (а=32,34). Расчет скорости проведем по формуле, аналогичной представленной ранее:

V₁=(13,01-13,86)/(360-420)=0,0141 гр/с

V₂=(9,00-13,53)/(60-120)=0,075 гр/с

Константа const. для этого случая равна произведению концентрации цинка на площадь поверхности испарения и составляет 9,42. Нанесем полученные данные на график, рисунок 5.7.

Определенные по графику значения а=4,32, b=-11000. Отсюда ko1=65,2 гр/см2с, E1= 90400 Дж.

Аналитическая процедура. Для моментов времени, когда степени протекания равны, составим систему уравнений:

V₁ = -ko1.exp(-E1/RT1).const;

V₂ = -ko1.exp(-E1/RT2).const;

Подстановка численных значений дает: ko1=33,90 гр/см2с, E1= 83331 Дж.

Если сравнить этот результат с тем, что был получен графическим методом, то мы убедимся, что хотя они и близки, но все-таки отличаются. Это произошло потому, что мы из всей кинетической кривой использовали по существу лишь одну точку. Устранить этот недостаток можно, определяя коэффициенты компьютерным методом.

Рассмотрим особенности кинетики основных пирометаллургических процессов (диссоциации, окисления, восстановления), термодинамику которых мы рассмотрели ранее.

Особенности кинетики диссоциации.

В пирометаллургии цветных металлов приходится довольно часто встречаться с диссоциацией сульфидов, оксидов, кар­бонатов и других солей. Разложение природных минералов в ходе нагревания представляет начальную стадию многих тех­нологических процессов. Диссоциация предшествует или соп­ровождает процессы восстановления металлов, их оксидов, окисления сульфидов, сульфидирования оксидов и др. Кине­тика процесса в ряде случаев может определять технико-экономические показатели всей технологии. Изучение общих закономерностей кинетики диссоциации и вскрытие механизма термического разложения дают в руки металлургов ключ к управлению этим процессом.

Реакции диссоциации соединений в твердом состоянии принадлежат к классу топохимических реакций, сопровождающихся кристаллохимическими превращениями в твердом теле твердое тело I твердое тело II + газ

При прямом течении процесс диссоциации проходит как минимум через следующие стадии: собственно диссоциацию, сопровождающуюся появлением в поверхностном слое адсорби­рованных молекул газа и образованием твердых растворов Ме—МеХ в соединениях; зарождение новой фазы и кристаллохимическое превращение на границе раздела; десорбцию и диффузию газовых молекул.

При диссоциации, например оксидов или сульфидов, пер­вая стадия сводится к переходу электронов от анионов О^2- или S^2- к катионам металла с последующим образованием га­зовых молекул из атомов. Эти процессы крайне сложны и в свою очередь распадаются на отдельные стадии. Стадии пер­вого этапа процессов диссоциации, как правило, изучены недостаточно. Для того чтобы прошла диссоциация вещества частицы соединений должны накопить запас энергии, необхо­димый для разрушения старых связей и образования новых. Потенциал ионизации всегда больше для последующих элект­ронов. Этим объясняется тот факт, что высшие оксиды и сульфиды диссоциируют всегда легче с меньшей затратой энергии.

Зарождение новой фазы и кристаллохимические превраще­ния являются вторым этапом процесса. Катионы и анионы за­кономерно чередуются в пространстве в оксидах или сульфи­дах. Такому положению отвечает известное равновесие сил, что определяет устойчивость кристалла. Термодинамический потенциал такой системы G₀. При повышении температуры происходит диссоциация соединения и возникают зародыши новой фазы. Химическая реакция сопровождается перестрой­кой одной кристаллической решетки в другую, что связано с преодолением определенного энергетического барьера. Иног­да наличие этого барьера может существенно тормозить про­цесс в целом.

Рассмотрим как происходит образование зародыша новой фазы в недрах старой— материнской. Теория этого процесса была развита Я.И.Френкелем. Начальная стадия разложения протекает без появления новой фазы, что связано с замет­ной величиной растворимости образующегося металла в окси­дах и сульфидах.

В случае нестехиометрических соединений, состав кото­рых относится к кислородной или серной области гомоген­ности, сначала происходит выделение летучих компонентов со смещением состава к металлической стороне области го­могенности.

Этот вопрос был подробно рассмотрен ранее при обсужде­нии строения этих соединений. После достижения предела насыщения происходят выпадение металла из твердого раст­вора, образование зародышей новой фазы.

Образование зародышей согласно теории Я.И. Френкеля связано с флуктуациями. В любой молекулярной, ионной или атомной системе, находящейся в тепловом равновесии в раз­личных точках непрерывно происходят отклонения тех или иных величин от их наиболее вероятных значений, так назы­ваемые флуктуации. Это вызвано наличием дефектов в струк­туре твердого тела, движением вследствие самодиффузии атомов (ионов) по вакансиям, перескоком частиц в межузлия, наличием дислокаций. Очевидно, с повышением темпера­туры количество таких флуктуации будет возрастать пропор­ционально возрастанию количества вакансий и увеличению скорости теплового движения частиц.

При известных условиях флуктуации могут привести в от­дельных точках твердого тела к переходу от стабильного состояния вещества к неустойчивому. Происходит образова­ние зародышей. Такие флуктуации называются гетерофазными

Если эти зародыши способны расти, то новая фаза выде­ляется из материнской, происходит распад раствора. Если же зародыши неустойчивы, то время их жизни оказывается очень коротким. Флуктуации, обеспечивающие сгущение ве­щества в каком-то объеме в один момент времени, в следую­щий момент вызовут его разрежение. Зародыш рассосется.

Очевидно, что рост зародыша возможен лишь в том слу­чае, если процесс будет идти с понижением термодинамичес­кого потенциала системы.

Появление новых частиц в недрах старой фазы нарушает симметрию межчастичного взаимодействия и вызывает местные деформации решетки и состояние напряжения. Оно характери­зуется энергией напряжения (межфазное натяжение), прихо­дящейся на единицу поверхности раздела.

Напряжение выражает тенденцию к перестройке исходной решетки в новую, которой отвечает более низкое значение энергии системы:

G₀ – G₁ = ΔG = mΔG’+Sσ

Таким образом, изменение изобарного потенциала системы складывается из изменения в объеме, приходящегося на одну молекулу ΔG’ (m - количество молекул новой фазы) и энер­гии напряжения Sσ.

Объем V и поверхность S частиц новой фазы, внедряющей­ся в решетку сульфида или оксида, определенным образом связаны с числом молекул.

Так, для сферических частиц объем одного зародыша V = 4/Зπr³ (r - радиус зародыша). В этом случае число моле­кул в одном зародыше можно определить из выражения m = V/V_m (V_m - объем одной молекулы). Тогда S = aV_m^2/3m^2/3 (а — коэффициент пропорциональности).

Общее изменение величины ΔG при диссоциации соединения с образованием одного сферического зародыша определяется из выражения: ΔG = m ΔG ' + aV_m^2/3m^2/3σ.

Закономерности изменения термодинамического потенциала системы при диссоциации соединения и возникновении новой фазы нередко анализируют с использованием такого физико-химического параметра системы, как химический потенциал µ. Такой подход позволяет проследить связь между теорией флуктуации, обшей термодинамикой процесса, размером зародышей, а в зависимости от этого, устойчивостью и ве­роятностью их роста.

Представим себе, что в процессе диссоциации соединения на его поверхности образуются зародыши кубической формы. Нетрудно показать, что ΔG системы при этом может быть оценено с помощью выражения

ΔG = (µ₂ - µ_1,3,4,5)ml³ + 6l²σ

где l — длина ребра куба одиночного зародыша; m — число молекул в зародыше; µ₂- химический потенциал металла в насыщенном растворе; µ_1,3,4,5- химический потенциал Me в растворах соединений по мере их насыщения (µ₅ > µ₄ > µ₃> µ₁; σ - межфазное натяжение на границе системы сое­динение — металл.