Лекция 13. Адсорбция
13.1. Уравнение адсорбции Гиббса
Строгое определение понятия адсорбции по Дж. Гиббсу: адсорбцией данного компонента на границе раздела двух фаз называется разность между фактическим количеством этого компонента в системе и тем его количеством, которое было бы в системе, если бы концентрации в обеих сосуществующих фазах были постоянны вплоть до некоторой геометрической поверхности, разделяющей их.
Эта разность может быть положительной или отрицательной. Она обозначается символом G (гамма) и имеет размерность моль/м2. Эту величину называют избыточной адсорбцией по Дж. Гиббсу.
Хотя в приведенном определении адсорбция отнесена к геометрической поверхности, не имеющей толщины (что удобно при выводе уравнений), фактически граница между фазами представляет собой очень тонкий слой (поверхностный слой), в котором все свойства отличаются от свойств объемных фаз и изменяются не скачкообразно, а непрерывно.
На рис. 13.1 показано возможное изменение концентрации вблизи границы раздела: концентрация компонента может быть как выше концентраций в обеих фазах (1), так и ниже (2) или иметь промежуточное значение. Эта область может рассматриваться как поверхностный слой. Таким образом, изучая границу раздела фаз, нужно рассматривать состояние трех фаз: двух объемных и одной поверхностной.
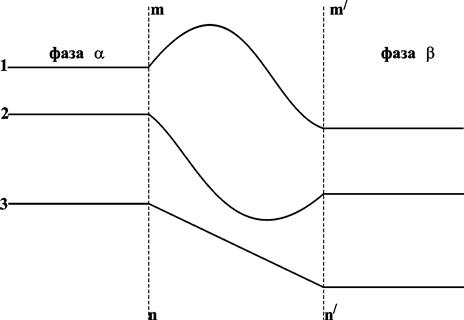
Рис. 13.1. Изменение концентрации компонентов у границы раздела фаз;
поверхностный слой – mn-m’n’
Уравнение, устанавливающее связь между всеми параметрами процесса адсорбции – величиной поверхностного натяжения s, концентрацией компонента [C] в одной из фаз, его адсорбцией Г, было выведено Дж. Гиббсом в 1876 г. Это уравнение является общим термодинамическим уравнением, справедливым для любых составов и природы поверхности раздела фаз.
Рассмотрим систему, состоящую из двух компонентов 1 и 2 и двух фаз a и b, разделенных поверхностью раздела с площадью S. Общее число молей каждого компонента в системе равно n1o и n2o. Если считать, что поверхностный слой не имеет толщины, т.е. представляет собой геометрическую поверхность, то обе объемные фазы будут иметь постоянный состав вплоть до этой геометрической поверхности. Обозначим число молей каждого компонента в каждой из этих фаз соответственно через n1a,n1b ; n2a,n2b. Так как на поверхности имеет место адсорбция, то, очевидно, n1o ¹ n1a + n1b и n2o ¹ n2a + n2b.
По вышеприведенному определению адсорбция каждого компонента Г1 и Г2 , отнесенная к единице площади поверхности, равна
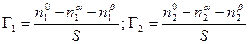 . (13.1)
. (13.1)
Чтобы найти Г1 и Г2, напишем уравнение энергии Гиббса для двух фаз a и b в отдельности и для всей системы в целом. В последнем случае, очевидно, нужно включить в уравнение член sdS:
dGa = - Sa dT + VadP + m1dn1a + m2dn2a;
dGa = - Sb dT + VbdP + m1dn1b + m2dn2b;
dGo = - So dT + VodP + sdS + m1dn1o + m2dn2o. (13.2)
Укажем на уравнение Гиббса-Дюгема, которое устанавливает связь между химическими потенциалами:
dG = - S dT + VdP + Smidn1 (P, T – постоянные). (13.3)
Тогда для бинарной системы получим
dG = m1dn1 + m2dn2. (13.4)
Интегрируя это уравнение при постоянных значениях m1 и m2, получим
G = m1n1 + m2n2. (13.5)
Следовательно,
dG = m1dn1 + m2dn2 + n1dm1 + n2dm2. (13.6)
Из (13.4) и (13.6) вытекает, что
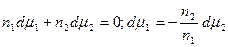 . (13.7)
. (13.7)
Это уравнение носит название уравнения Гиббса-Дюгема и связывает изменение химических потенциалов компонентов. Тогда с учетом уравнения Гиббса-Дюгема и поверхностных явлений получаем:
n1adm1 + n2adm2 = 0;
n1bdm1 + n2bdm2 = 0; (13.8)
Sds +n1odm1 + n2odm2 = 0.
Сложение двух первых уравнений и вычитание полученной суммы из третьего дает
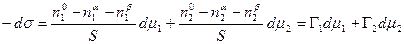 . (13.9)
. (13.9)
В качестве примера рассмотрим две конкретные системы: двухкомпонентный жидкий раствор, находящийся в равновесии со своим двухкомпонентным насыщенным паром, и твердое тело, находящееся в равновесии с однокомпонентным газом, совершенно не растворимым в этом твердом теле.
Поскольку в первом случае точное положение разделяющей геометрической поверхности несколько условно, то можно выбрать положение ее, при котором
Г1 = 0,
тогда
ds = - Г2dm2. (13.10)
Во втором случае вследствие нерастворимости газа в объеме твердого тела, объемные свойства этого тела, в частности его химический потенциал, не изменяются при адсорбции. Приписывая твердому телу индекс 1, имеем:
m1 = const и dm1 = 0,
поэтому
ds = - Г2dm2. (13.11)
В обоих случаях получено одно и то же уравнение. Поэтому можно считать, что адсорбционное уравнение Гиббса имеет вид:
ds = Г2dm2.(13.12)
Оно является основным в учении о поверхностных явлениях.
Рассмотрим далее реальный раствор. Для реального раствора
m = mо(Т) + Rtlna,
где а – активность, тогда:
dm = RТ d lna.
Подставив это значение в уравнение (13.12), получим:
ds = - Г Rt d lna,
или
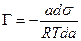 . (13.13)
. (13.13)
В разбавленных растворах а » С (где С – концентрация)
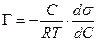 , (13.14)
, (13.14)
а для идеального или разреженного идеального газа
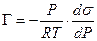 . (13.15)
. (13.15)
Уравнение (13.14) показывает, что если при адсорбции поверхностное натяжение s уменьшается с ростом концентрации С, т.е. ds/dC < 0, то адсорбция Г – положительна. Это соответствует поверхностно-активным веществам. Наоборот, если s растет с ростом С, то ds/dC > 0 и Г – отрицательно. Это соответствует поверхностно-инактивным веществам. Если известна зависимость s от С (т.е. изотерма поверхностного натяжения s = f(C) , то по уравнению Гиббса можно для каждого значения концентрации найти ds/dC и по уравнению Гиббса вычислить значение Г, т.е. построить изотерму адсорбции.
13.2. Обзор сорбционных явлений
Адсорбция на границе раздела твердое тело/газ. В общем случае явления, связанные с перераспределением веществ между различными частями гетерогенной системы, называются сорбцией. Сорбция (от лат. sorbeo – сгущать) – это изменение концентрации (часто увеличение) либо у поверхности раздела фаз (адсорбция), либо в объеме одной из фаз (абсорбция). Например, образование раствора за счет поглощения НСl (газа) и поглощение газа металлом (абсорбция). Поверхностная сорбция – адсорбция.
Твердое тело, у поверхности которого происходит адсорбция, называется адсорбентом, адсорбирующийся газ или адсорбирующийся компонент жидкого раствора – адсорбтивом, а адсорбированое вещество – адсорбат.
В строгом определении адсорбции она рассматривается как избыток вещества вблизи поверхности по сравнению с равным объемом вдали от нее. В ряде случаев удобнее рассматривать не избыток, а все количество адсорбата вблизи поверхности. Это количество обозначают символом а и называют полным содержанием, или просто адсорбцией (без указания гиббсова). Так как для пористых твердых тел бывает затруднительно знать величину поверхности, то часто адсорбцию относят не к единице поверхности, а к единице массы (моль/кг или моль/г).
Адсорбция самопроизвольна и протекает при Р = const со снижением энергии Гиббса, а при V = const – со снижением энергии Гельмгольца. Однако при этом происходит не выравнивание концентраций по всему объему системы, а увеличение разности концентраций между газовой фазой (раствором) и поверхностью. Одновременно уменьшается подвижность сорбирующихся молекул. Оба фактора ведут к уменьшению энтропии (DS<0).
По основному уравнению термодинамики находим
DH = TDS + DG (13.16)
Если величины DS и DG – отрицательны, то значение DН – отрицательно и процесс является экзотермическим.
Важной характеристикой адсорбции является теплота адсорбции. Она является мерой интенсивности адсорбционных сил – сил взаимодействия молекул адсорбата с поверхностью адсорбента и между собой.
Интенсивность взаимодействия адсорбент-адсорбат зависит от состояния адсорбента и от того, какое количество адсорбата уже адсорбировано (от заполнения поверхности). Поэтому различают два основных понятия – интегральная и дифференциальная теплота адсорбции.
Интегральной теплотой адсорбции Q называется полное количество теплоты, выделяющейся при адсорбции n молей адсорбата. Ее относят к единице массы адсорбента (Дж/кг). Дифференциальной теплотой адсорбции q называют отнесенное к 1 молю адсорбата дополнительное количество теплоты, выделяющейся при адсорбции бесконечно малого количества адсорбата:
 или
или 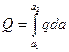 . (13.17)
. (13.17)
Типичные зависимости интегральной и дифференциальной теплоты адсорбции от количества адсорбированного вещества представлены на рисунке 13.2. Прямые 1 для Q и 2 для q соответствуют зависимости Q = ka. Как правило, такая прямая зависимость не наблюдается (она возможна лишь при q = const). Фактически вследствие неоднородности поверхности адсорбента адсорбция происходит сначала на наиболее активных участках поверхности с наибольшим значением дифференциальной теплоты; при больших заполнениях q уменьшается. Это приводит к некоторому замедлению роста Q. Возможен и третий случай. Вследствие взаимного притяжения адсорбированных молекул уменьшается расстояние между ними и дифференциальная теплота адсорбции повышается (кривая 3).
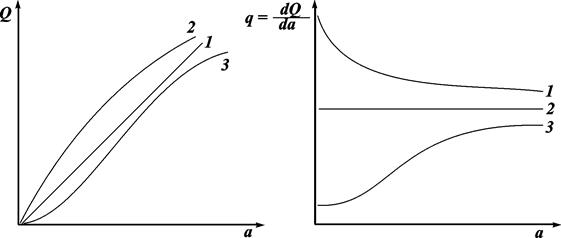
Рис. 13.2. Зависимость интегральной и дифференциальной теплоты адсорбции от количества адсорбированного вещества
13.3. Природа адсорбционного взаимодействия
Величина адсорбции – функция природы адсорбента и адсорбата и зависит от силы взаимодействия между ними. При адсорбции взаимодействуют молекулы, принадлежащие разным фазам, а на границе раздела фаз неизбежно существует асимметрия сил взаимодействия. Кроме того, молекулы адсорбата взаимодействуют не с единичной молекулой адсорбента, а с их совокупностью. Благодаря этому силы взаимодействия в зависимости от их природы могут либо возрастать, либо ослабевать.
Адсорбцию делят на физическую и химическую (хемосорбцию). Как правило, физическая адсорбция обусловлена межмолекулярными (ван-дер-ваальсовыми) силами. В простейшем случае взаимодействие неспецифично, т.е. речь идет об универсальных, дисперсионных силах. Молекулы на поверхности не теряют своей индивидуальности.
Дисперсионное взаимодействие не зависит от температуры. Важным свойством дисперсионных сил является их аддитивность; сила взаимодействия между двумя молекулами не зависит от присутствия других молекул. Аддитивность проявляется в том, что суммируются силы взаимодействия молекул адсорбата со всеми близлежащими атомами поверхности адсорбента. Поэтому при адсорбции пористыми адсорбентами вклад дисперсионных сил в общее взаимодействие оказывается существенно бóльшим. При адсорбции неполярных веществ на полярном адсорбенте (ионный кристалл) к дисперсионным силам притяжения добавляются индукционные силы притяжения диполя, индуцированного электростатическим полем адсорбента. Индукционное притяжение возникает и при адсорбции полярных молекул на неполярном адсорбенте.
Адсорбция полярных молекул на полярном адсорбенте вызывает ориентационное кулоновское взаимодействие диполя адсорбата с электростатическим полем адсорбента. Энергия индукционных, ориентационных и дисперсионных сил при парном взаимодействии обратно пропорциональна шестой степени расстояния между центрами взаимодействующих атомов. Однако ориентационные и индукционные взаимодействия, будучи электростатическими, не являются аддитивными. Так, появление третьей молекулы в поле взаимодействия двух других изменяет ориентацию молекулы и ослабляет эти взаимодействия. Поэтому энергия взаимодействия молекулы адсорбата с поверхностью адсорбента может оказаться меньше, чем энергия ее взаимодействия с одним центром на поверхности. При адсорбции пористыми адсорбентами индукционное и ориентационное взаимодействия вносят меньший вклад. Поэтому наибольшую роль чаще всего играет дисперсионное взаимодействие. Для неполярных или слабополярных молекул его вклад может быть стопроцентным.
Неспецифический характер взаимодействий, вызывающих физическую адсорбцию, определяет и основные признаки этого явления. Равновесие при физической адсорбции устанавливается быстро и обратимо. Теплота физической адсорбции превышает теплоту конденсации обычно не более чем на ~20 кДж/моль.
Химическая адсорбция имеет место, когда молекулы адсорбата вступают в химическое взаимодействие с поверхностью адсорбента с образованием
поверхностных химических соединений, но без образования новой объемной
фазы. Она гораздо более избирательна и чувствительна к химической природе адсорбата и адсорбента. Теплоты хемосорбции обычно велики (100‑200 кДжмоль).
Хемосорбция может протекать довольно медленно, со скоростью, определяемой наличием некоторого активационного барьера. Поэтому ее часто называют «активированная адсорбция». При низких температурах скорость хемосорбции обычно мала. Хемосорбция, как правило, необратима.
Существует большое многообразие форм адсорбции, переходных между физической и химической адсорбцией. Так, например, широко распространенным видом такого переходного взаимодействия является образование водородной связи при адсорбции. Это характерно для адсорбентов, содержащих на поверхности гидроксильные группы (силикагель, алюмогель и др.). Для этого пограничного типа адсорбции теплота составляет обычно 20-40 кДж/моль.
В связи с разнообразием адсорбционных сил единая теория адсорбции, позволяющая на основе предположений о механизме процесса составить общее математическое описание, пока отсутствует.
13.4. Термическое уравнение адсорбции.
Изотерма адсорбции
Для данной пары адсорбент – адсорбат величина адсорбции а или Г определяется двумя основными термодинамическими параметрами состояния: температурой Т и давлением Р для газообразного состояния адсорбата или Т и концентрацией С при адсорбции из растворов. Все три величины связаны функциональной зависимостью, называемой термическим уравнением обратимой сорбции:
f = (a,Р,T) = 0 или j = (Г,С,Т) = 0. (13.18)
В теории адсорбции особенно часто рассматривают адсорбционное равновесие при условии, что один из параметров, входящих в термическое уравнение, поддерживается постоянным. Например, а = f(P)Т или Г = j (С)Т. Адсорбия, если она выражена не как избыток, а как полное содержание, всегда возрастает с повышением равновесного давления (концентраци). Так как адсорбция – процесс экзотермический, то при повышении температуры величина адсорбции снижается.
Уравнение, связывающее величину адсорбции с температурой при постоянном равновесном давлении а = f(T)P или постоянной равновесной концентрации Г = j(Т)С, носит название соответственно изобары или изопикны адсорбции. Уравнение вида Р = f(Т)а (изостера адсорбции) связывает равновесное давление с температурой при постоянном адсорбированном количестве.
Переход вещества из газовой фазы в адсорбированное состояние в известном смысле аналогичен фазовому переходу пар-жидкость. Поэтому для такого перехода может быть выведена формула, аналогичная формуле Клаузиуса-Клапейрона. Однако в этом случае в формулу входит частная производная давления по температуре при постоянном значении адсорбции (¶Р/¶Т)a:
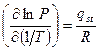 , (13.19)
, (13.19)
где qst – изостерическая теплота адсорбции, которая очень близка к выведенной ранее дифференциальной теплоте.
Для математического описания адсорбции необходимо уравнение, которое связывает зависимость равновесной величины адсорбции от концентрации адсорбата в объемной фазе при различных температурах, а также правильно предсказывает изменение теплоты адсорбции от заполнения адсорбента.
Однако форма изотермы адсорбции на твердых телах зависит от многих параметров: свойств адсорбента и адсорбата, взаимодействия адсорбтив/адсорбат, взаимодействия молекул адсорбата между собой в газовой фазе и в адсорбированном состоянии. В области малых давлений (концентраций) и малых заполнений поверхности взаимодействия между молекулами адсорбата незначительны и зависимость а = f(P)T сводится к простейшей форме, называемой законом Генри:
а = kP или а = kC. (13.20)
Коэффициент пропорциональности k – коэффициент Генри – является мерой интенсивности адсорбции. При больших давлениях (концентрациях) и больших заполнениях адсорбцию часто выражают эмпирическим уравнением Фрейндлиха
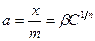 , (13.21)
, (13.21)
где х – количество адсорбированного вещества, m – масса адсорбента, b и n – константы, характерные для каждой адсорбционной системы. Причем 1/n всегда правильная дробь (0 < 1/n < 1). По Г. Фрейндлиху, n не зависит от заполнения, хотя это не вполне точно. Этим уравнением часто пользуются для ориентировочной оценки адсорбции.
13.5. Мономолекулярная адсорбция и изотерма
Ленгмюра
Первое теоретическое уравнение изотермы адсорбции было предложено И. Ленгмюром в 1914 году. Теория Ленгмюра основана на трех основных положениях:
Адсорбция происходит на дискретных адсорбционных центрах, которые могут иметь различную природу.
При адсорбции соблюдается строгое стехиометрическое условие – на одном центре адсорбируется одна молекула.
Адсорбционные центры энергетически однородны и независимы, т.е. адсорбция на одном центре не влияет на адсорбцию на других центрах.
На основании этих положений скорость адсорбции Vaдc пропорциональна давлению газа и числу свободных центров. Если общее число центров аm, то при адсорбции, равной а, число свободных центров равно (аm – а).
Поэтому
Vaдc = kaдc × P × (am – a). (13.22)
Наряду с адсорбцией идет процесс десорбции:
Vдес. = kдес. × а. (13.23)
При равновесии Vaдc = Vдес или
kaдc × P × (am – a) = kдес. × а. (13.24)
Обозначим kдес./ kадс. = b, а а/аm = Q, где Q – относительное заполнение поверхности, получим:
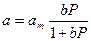 или
или 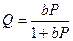 . (13.25)
. (13.25)
Это уравнение изотермы адсорбции называется уравнением Ленгмюра. Константа b носит название константы адсорбционного равновесия, или адсорбционного коэффициента.
Константа равновесия связана со стандартными изменениями энергии Гиббса. Если
RTlnb = –DGo, так как DGo = DHo + TDSo,
то
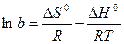 . (13.26)
. (13.26)
Следовательно
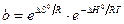 . (13.27)
. (13.27)
Таким образом, адсорбционный коэффициент b связан со стантартной энтропией DS° и со стандартной теплотой адсорбции q = –DH°.
Очень часто аm называют «емкость монослоя». На рис.13.3 показана кривая, выражающая изотерму адсорбции по Ленгмюру
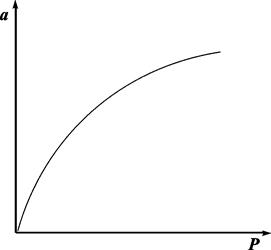
Рис. 13.3. Изотерма адсорбции по Ленгмюру
При очень малых заполнениях и, следовательно, очень малых давлениях Р в знаменателе, согласно (13.25), bр<< 1. Поэтому в этой области а = аmbp, т.е. переходит в уравнение Генри. При очень высоких давлениях bp >> 1 и а = аm, т.е. величина адсорбции перестает зависеть от давления, поскольку все центры уже заняты.
Для расчета параметров am и b уравнение Ленгмюра представляют в виде
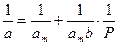 . (13.28)
. (13.28)
Тангенс угла наклона этой линии равен 1/amb, а отрезок, отсекаемый на оси ординат, равен 1/am.
Уравнение Ленгмюра, полученное на основании модели локализованной адсорбции газов на поверхности твердого тела, часто хорошо описывает адсорбцию растворенных веществ на поверхности жидкости (поверхность раздела раствор/газ), при которой адсорбция не локализована, так как молекулы подвижны и образуют двумерную газо- или жидкообразную пленку.
Обусловлено это тем, что основные положения модели Ленгмюра соблюдаются при адсорбции из растворов: поверхность жидкости идеально однородна, взаимодействие адсорбированных молекул в адсорбционном слое мало отличается от их взаимодействия в растворе. Оно к тому же ослаблено за счет взаимодействия молекул растворенного вещества с молекулами растворителя и практически не влияет на адсорбцию.
Уравнение Ленгмюра связано с уравнением состояния адсорбционной пленки – уравнением Гиббса. Так,
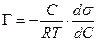 ,
,
а по уравнению Ленгмюра
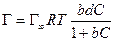 ;
;
тогда
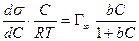
или
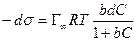 . (13.29)
. (13.29)
После интегрирования в пределах от sо до s и от 0 до С получим:
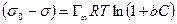 ,
,
и, наконец,
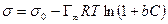 , (13.30)
, (13.30)
где Г¥ связано с площадью, занимаемой 1 моль адсорбированного вещества в мономолекулярном слое, следующим соотношением: 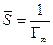 .
.
Дата добавления: 2016-02-09; просмотров: 4188;
