Лекция 10. Электрохимия
10.1. Введение в электрохимию
Электрохимия изучает химические реакции, протекающие под влиянием электрического тока, и процессы генерирования электрической энергии, происходящие в результате протекания химических реакций. Оба типа этих процессов сопровождаются взаимопревращениями электрической и химической энергии.
Все электрохимические процессы можно подразделить на две группы: процессы электролиза, при которых под воздействием внешнего источника электрической энергии происходят химические реакции, и процессы генерирования электрической энергии в результате протекания химической реакции.
В процессах первой группы электрическая энергия превращается в химическую. В процессах другой группы, наоборот, химическая энергия превращается в электрическую.
Примерами обоих типов могут служить процессы, протекающие в аккумуляторах. Так, при работе свинцового аккумулятора как генератора электрической энергии происходит реакция
Pb + PbO2 + 4H+ + SO42- ® 2PbSO4 + 2H2O.
В результате этой реакции выделяется энергия, которая и превращается в электрическую энергию. Если аккумулятор разрядится, то его заряжают, пропуская через него постоянный электрический ток в обратном направлении. В результате протекает химическая реакция
2PbSO4 + 2H2O ® Pb + PbO2 + 4H+ + SO42-.
В этом случае электрическая энергия превращается в химическую.
Все электрохимические реакции происходят при протекании электрического тока в цепи. Эта цепь слагается из последовательно соединенных металлических проводников и раствора (расплава) электролита. В металлических проводниках переносчиками тока являются электроны, в электролитах – ионы. Непрерывность протекания тока в цепи обеспечивается, если происходят процессы на электродах, т.е. на границе металл–электролит. Отличие электрохимических процессов от химических заключается в пространственном разделении процессов окисления и восстановления.
Основной характеристикой электрохимической системы является электродвижущая сила (ЭДС) – разность потенциалов между двумя металлическими электродами, которая измеряется при протекании обратимых процессов в системе.
Электрохимическая система, генерирующая электрическую энергию за счет протекающих в ней химических реакций, называется гальваническим элементом.
Процессы, при которых за счет электрической энергии от внешнего источника происходят химические превращения, называются электролизом. Электрод, на котором происходит процесс окисления, называется анодом, а тот, на котором происходит процесс восстановления, – катодом.
В гальваническом элементе анод обычно называют отрицательным полюсом, катод – положительным полюсом.
10.2. Термодинамика электрохимических систем
Электродвижущая сила гальванического элемента слагается из алгебраической суммы скачков потенциала на границах всех разнородных фаз системы:
| М1 | |||
| М1 | |||
| М2 | Эл II | Эл I | М1 |
На границе металл I – электролит I, электролит I – электролит II; электролит II – металл II и скачка потенциала на границе металл I – металл II (контактная разность потенциалов).
Если два металла замкнуты с помощью проводника (М III), то сумма скачков потенциала e (МI – MIII) +e (MШ – МII) равна скачку потенциала e (МI ‑ MII). Скачок потенциала на границе металл – раствор электролита является результатом перехода заряженных частиц через поверхность раздела фаз. При таком переходе, помимо химической работы, совершается работа электрическая. Соответственно состояние заряженной фазы в расчете на 1 моль компонента i характеризуется так называемым электрохимическим потенциалом `mi:
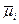 = mi + zFFI, (10.1)
= mi + zFFI, (10.1)
где mi – химический потенциал I-го компонента данной фазы; zFFi – электрическая энергия 1 моль заряженных частиц этого компонента в данной фазе; F – число Фарадея, т.е. суммарный заряд одного эквивалента ионов, несущих заряд; z, Fi – разность электрических потенциалов между точкой внутри фазы и бесконечно удаленной точкой в вакууме, потенциал которой считается равным нулю.
Равновесие между заряженными частицами I-го компонента в двух фазах А и В наступает при равенстве их электрохимических потенциалов 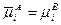 . Отсюда для равновесия
. Отсюда для равновесия
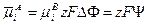 , (10.2)
, (10.2)
где Y – разность потенциалов между точками внутри фаз А и В; Y называется гальвани-потенциалом.
Скачок потенциала на границе металл – металл (межфазный гальвани-потенциал) возникает вследствие преимущественного перехода электронов из одной металлической фазы в другую. Его приравнивают к контактной разнице потенциалов. Скачок потенциала между двумя контактирующими жидкостями называется фазовым жидкостным потенциалом, если растворителем являются две несмешивающиеся жидкости. Если растворы различаются только природой или концентрацией электролита, то возникающая разность потенциалов называется диффузионным потенциалом.
Разность внутренних потенциалов между металлом и раствором называется нернстовским потенциалом. В общем случае ЭДС состоит из скачков потенциала между двумя металлами, двух нернстовских потенциалов (на границе металл – раствор) и гальвани-потенциала (раствор – раствор). Отметим, что контактная разность потенциалов не всегда входит составной частью в ЭДС. Так, если оба металлических электрода одинаковы, а оба электролита различны, то контактная разность потенциалов равна нулю. Нулю равен диффузионный потенциал в системах, в которых два металлических электрода находятся в контакте только с одним раствором электролита.
В соответствии с первым началом термодинамики взаимопревращение химической и электрической энергии происходит в строго эквивалентных количествах. Но если пропускать электрический ток через электролит, то не вся электрическая энергия превратится в химическую; часть ее превратится в теплоту в форме джоулева тепла q, которое равно
q = I2Rt, (10.3)
где q – количество теплоты; R – электрическое сопротивление электролита;
I – величина тока; t – время.
Если электрические процессы протекают термодинамически обратимо при силе тока I, равной нулю, то джоулево тепло не выделяется.
В этом случае гальванический элемент выполняет максимальную работу, которая равна изменению энергии Гиббса, взятому со знаком минус:
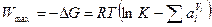 , (10.4)
, (10.4)
где К – константа равновесия реакции, ai – активность i-го участника реакции.
Электрическая работа равна работе химической реакции:
Wmax = –DG = zFE, (10.5)
где Е – ЭДС гальванического элемента.
Сопоставим (12.4) и (12.5):
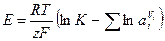 . (10.6)
. (10.6)
Для идеальных (разбавленных) растворов
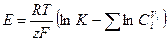 . (10.7)
. (10.7)
Уравнения (10.6) и (10.7) позволяют вычислить ЭДС гальванического элемента по данным о константе равновесия и концентрации всех участников реакции. Или, зная ЭДС, можно вычислить константу равновесия. Величину Е выражают в вольтах.
Сопоставим уравнение (10.5) и уравнение Гиббса-Гельмгольца
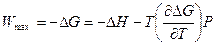 . (10.8)
. (10.8)
Продифференцировав (10.5) по Т, получим:
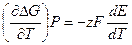 . (10.9)
. (10.9)
z и F – не зависят от температуры. тогда
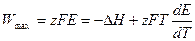 ; (10.10)
; (10.10)
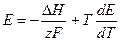 . (10.11)
. (10.11)
Уравнения (10.11) и (10.10) позволяют легко и достаточно точно определять величину теплового эффекта (DН) химической реакции, протекающей в гальваническом элементе по величине ЭДС и производной 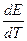 . Последнюю находят путем измерения Е при разных температурах. Параметр
. Последнюю находят путем измерения Е при разных температурах. Параметр 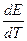 (температурный коэффициент ЭДС) может быть положительным или отрицательным. В первом случае (
(температурный коэффициент ЭДС) может быть положительным или отрицательным. В первом случае ( 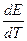 > 0) максимальная работа электрического тока превышает убыль энтальпии (-DН) и поэтому при работе гальванического элемента его температура будет понижаться. Во втором случае (
> 0) максимальная работа электрического тока превышает убыль энтальпии (-DН) и поэтому при работе гальванического элемента его температура будет понижаться. Во втором случае ( 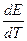 < 0), наоборот, температура электрохимической системы будет повышаться.
< 0), наоборот, температура электрохимической системы будет повышаться.
10.3. Электродный потенциал
При погружении металлической пластинки (электрода) в раствор электролита между пластинкой и раствором возникает скачок потенциала. Почему это происходит? в узлах кристаллической решетки металла находятся положительно заряженные ионы. В результате взаимодействия с полярными молекулами растворителя они отрываются и переходят в раствор. Параллельно происходит и обратный процесс. Если в первый момент скорость процесса перехода ионов из раствора в металл меньше скорости прямого перехода, то металл приобретает избыточный отрицательный заряд. Положительно заряженные ионы не удаляются от поверхности металла, а накапливаются у его поверхности. В результате образуется двойной электрический слой, в котором и возникает скачок потенциала.
Возможна и такая ситуация, когда скорость перехода ионов из раствора больше скорости перехода ионов в раствор. В этом случае поверхность металла зарядится положительно. Со временем и в том, и в другом случае в системе установится равновесие, поскольку переход в раствор и из раствора каждого последующего иона будет сопряжен с преодолением все большего энергетического барьера, связанного с возрастанием заряда металла (например, отрицательного при переходе ионов в раствор).
Таким образом, по мере увеличения отрицательного заряда будет уменьшаться разность электрохимических потенциалов `mм и `mр и разность скоростей V1 и V2. Изменение электрохимических потенциалов будет сопровождаться изменением скачка потенциала на границе металл – раствор. В конце концов `mм =`mр и установится динамическое равновесие.
Такая картина может быть экспериментально подтверждена с помощью радиоактивных индикаторов. Например, это было сделано с использованием висмута, содержащего радиоактивный изотоп.
Условились считать заряд электрода по заряду металла. Если металлическая пластинка заряжена отрицательно, то электрод считается отрицательным. Однако в электрохимической системе (гальваническом элементе), состоящей из двух электродов, независимо от знака заряда каждого электрода знак «плюс» электрода определяется относительной заряженностью электродов, составляющих элемент.
Переход ионов металла в раствор (анодный процесс):
М ® Мz+ + Ze-.
Переход ионов в металл (катодный процесс):
Мz+ + Ze-® М.
Так как оба процесса (прямой и обратный) связаны с переносом электрического заряда, то их скорости эквивалентны определенной величине тока I. Для расчетов обычно величину тока относят к единице поверхности электрода S. Это отношение называют плотностью тока:
i = 1/S. (10.12)
В момент равновесия скорости переноса одинаковы. Тогда при условии, что Sk = Sa (одинаковы) и величина анодной и катодной плотностей тока составляет
ia + ik = io,
где io – ток обмена, который характеризует кинетику обмена в момент равновесия, максимальная работа перехода ионов из металла в раствор в момент равновесия при р = const равна:
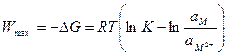 , (10.13)
, (10.13)
где ам2+ – активность ионов металла в растворе, ам – активность ионов металла в металле. Последняя равна 1. Электрическая работа при этом равна
Wmax = –DG = ZFe, (10.14)
где e – величина скачка потенциала на границе металл-электролит. Сопоставив (10.13) и (10.14), получим:
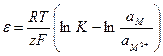 . (10.15)
. (10.15)
Величину скачка потенциала, как ЭДС, выражают в вольтах. Помня, что ам = 1, и перейдя к десятичным логарифмам, получим:
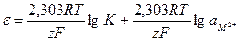 . (10.16)
. (10.16)
При постоянной температуре первый член в правой части содержит только постоянные величины и, следовательно, является постоянной величиной. Обозначим ее через eо. Тогда
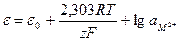 . (10.17)
. (10.17)
Определим физический смысл величины eо.. Если активность потенциал-определяющих ионов равна единице, т.е. амZ+ = 1, в этом случае eо = e, т.е. eо – это электродный потенциал, который возникает при погружении металла в раствор, в котором активность ионов металла равна 1 моль/л. Эта величина получила название стандартного электродного потенциала. Уравнение (10.17) было впервые выведено в 1890 году В. Нернстом и получило название уравнения Нернста.
Так как не существует ни теоретических, ни экспериментальных методов определения величины eо, то его значения становятся определенными только при выборе условного нуля отсчета. В качестве такового выбран потенциал стандартного водородного электрода. Потенциалы всех остальных электродов сравниваются с потенциалом стандартного водородного электрода.
Величина ЭДС, измеренная по отношению (в гальваническом элементе) к стандартному водородному электроду, и есть величина электродного потенциала по водородной шкале.
10.4. Двойной электрический слой на границе
между металлом и раствором электролита
Процессы электрохимического окисления и восстановления связаны с переносом электрона через поверхностный слой на границе между металлическим электродом и раствором, т.е. через двойной электрический слой.
Образующийся двойной слой подобен плоскому конденсатору, расстояние между обкладками которого определяется величиной радиуса ионов. такая упрощенная картина, предложенная Г. Гельмгольцем, справедлива только при больших концентрациях растворов электролитов и больших величинах плотности заряда электрода. В большинстве реализуемых случаев строение двойного слоя отличается от описанного.
В результате электростатического притяжения ионов заряженной поверхностью, с одной стороны, и хаотического теплового движения молекул, под влиянием которого ионы стремятся равномерно распределиться в растворе, – с другой, ионная обкладка приобретает диффузное строение. Концентрация ионов, несущих заряд, противоположный заряду поверхности металла, уменьшается по мере удаления от поверхности, а концентрация ионов, имеющих заряд, одинаковый по знаку с зарядом металла, возрастает по мере удаления от поверхности (рис. 10.1).
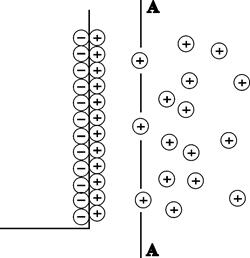
Рис. 10.1. образующийся двойной слой можно подразделить на плотную часть (слой Гельмгольца), образуемый ионами, прилегающими непосредственно к поверхности металла, и диффузную часть (диффузный слой)
образующийся двойной слой можно подразделить на плотную часть (слой Гельмгольца), образуемый ионами, прилегающими непосредственно к поверхности металла, и диффузную часть (диффузный слой).
В растворах электролитов толщина диффузного слоя составляет несколько нанометров (или доли нанометра). В разбавленных электролитах она может быть существенно больше, а в чистой воде достигает 1000 нм. Плотный двойной слой можно описать уравнением плоского конденсатора
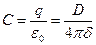 , (10.18)
, (10.18)
где 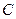 – емкость, относится к 1 см2 поверхности;
– емкость, относится к 1 см2 поверхности;
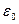 – разность потенциалов между металлом и раствором;
– разность потенциалов между металлом и раствором;
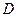 – диэлектрическая проницаемость;
– диэлектрическая проницаемость;
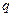 – плотность заряда;
– плотность заряда; 
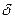 – толщина плотной части двойного слоя.
– толщина плотной части двойного слоя.
Величина поверхностного натяжения на границе металл – раствор изменяется при наложении потенциала. Это позволяет определять емкость двойного слоя по изменению зависимости поверхностного натяжения 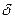 на границе металл – раствор от потенциала. Кривая, описывающая указанную зависимость, называется электрокапиллярной кривой (рис. 10.2).
на границе металл – раствор от потенциала. Кривая, описывающая указанную зависимость, называется электрокапиллярной кривой (рис. 10.2).
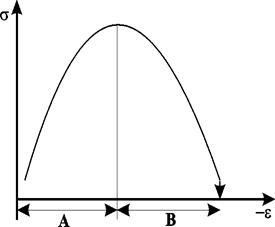
Рис. 10.2. Электрокапиллярная кривая. Область А – двойной слой из анионов; область В – двойной слой из катионов
Дифференциальное уравнение электрокапиллярной кривой, построенное термодинамическим путем, имеет вид
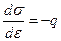 . (10.19)
. (10.19)
Продифференцировав уравнение (10.19) по 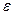 , найдем:
, найдем:
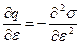 . (10.20)
. (10.20)
Таким образом, дифференциальная емкость равна второй производной поверхностного натяжения по потенциалу, взятой с обратным знаком.
10.5. Зависимость плотности заряда
от концентрации электролита
Впервые количественные расчеты зависимости плотности заряда от концентрации электролита в растворе и потенциале электрода, учитывающие диффузный характер двойного слоя, были выполнены Ж. Гуи. Заметим, что общая толщина двойного слоя 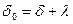 , где
, где 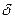 – толщина плотной части двойного слоя, а
– толщина плотной части двойного слоя, а 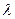 – толщина диффузной части. При больших концентрациях электролита
– толщина диффузной части. При больших концентрациях электролита 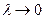 и
и 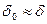 . Толщина диффузной части двойного слоя возрастает с уменьшением концентрации электролита и повышением температуры. При равных температуре и концентрации толщина диффузной части тем больше, чем меньший заряд несут ионы, концентрирующиеся в двойном слое.
. Толщина диффузной части двойного слоя возрастает с уменьшением концентрации электролита и повышением температуры. При равных температуре и концентрации толщина диффузной части тем больше, чем меньший заряд несут ионы, концентрирующиеся в двойном слое.
Диффузную часть двойного слоя принято называть слоем Гуи. В своих расчетах Ж. Гуи рассматривал ионы как точечные заряды. Позднее было показано, что такое представление совершенно неприменимо для плотной части двойного слоя, так как центр иона не может подойти к поверхности металла на расстояние меньшее, чем его радиус. Отсюда, в частности, вытекает, что в плотном слое потенциал изменяется линейно с расстоянием и, следовательно, градиент потенциала в этом слое сохраняет постоянную величину Y¤d (где Y – изменение потенциала в двойном слое).
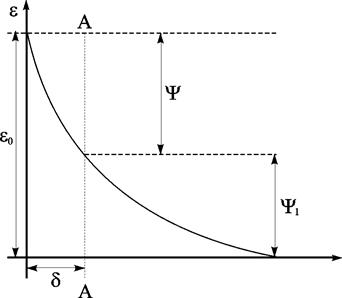
Рис. 10.3. Изменение потенциала в плотной и диффузной частях двойного слоя. Линия АА – граница между плотным и диффузным слоем
Изменение Y1 (потенциала) в диффузном слое происходит по некоторой кривой. Это изменение представляет собой разность потенциалов между границей плотной части двойного слоя АА и точкой в растворе, в которой концентрация Са = Ск. Общая разность потенциалов между металлом электролитом e° равна e° = Y + Y1 (рис.10.3).
Дата добавления: 2016-02-09; просмотров: 3247;
