Лекция 7. Растворы электролитов
7.1. Общие сведения о теории
электролитической диссоциации
«В конце концов мы должны признать, что ионная теория неполна, но в химии редко удается достичь совершенства. Наши научные теории совсем не похожи на законы, действующие, подобно сжатым пружинам, сразу же и неумолимо. Наши теории создаются медленно и постепенно, и мы должны честно признать, что ионная теория пока еще переживает пору своей юности. Вместо того, чтобы судить ее по строгим меркам совершенства, давайте просто спросим, чего она уже достигла и что она еще может дать науке», эти слова принадлежат Г. Льюису.
Теория электролитической диссоциации ныне стала одной из незыблемых основ наших научных представлений, и трудно поверить, что докторская диссертация С. Аррениуса, в которой он в 1884 году изложил эту теорию, была принята в университете города Уппсала (Швеция) с наинижайшей из возможных оценок.
В дальнейшем идеи Аррениуса встречали не столько противодействие, сколько полное пренебрежение, но, в конце концов, благодаря объединенным усилиям Я. Вант-Гоффа и В. Оствальда они завоевали всеобщее признание.
Важным вкладом в эту теорию стали последующие работы Ф.Х. Гроттуса, Н.Н. Каяндера и др.
Для обоснования гипотезы электролитической диссоциации имело значение сопоставление: 1) способности разбавленных водных растворов солей, кислот, оснований проводить электрический ток и 2) систематических отклонений некоторых свойств (температуры замерзания, температуры кипения, давления насыщенного пара, осмотического давления и др.) этих растворов и таких же свойств других разбавленных растворов. Была обнаружена количественная взаимосвязь между отклонениями в этих свойствах и способностью проводить электрический ток. Растворы, обнаруживающие большее отклонение в названных свойствах, обладают в общем и большей электропроводностью.
Гипотеза Аррениуса дала возможность объяснить многие особенности в химических свойствах растворов электролитов (реакции гидролиза, значение концентрации водородных ионов и др.). Согласно гипотезе электролитической диссоциации, молекулы солей, кислот и оснований при растворении их в воде претерпевают диссоциацию на ионы.
Однако в гипотезе Аррениуса раствор электролитов рассматривался по существу как механическая смесь из молекул растворителя и ионов и молекул электролита, т.е. в этой гипотезе не находило отражения взаимодействие между всеми этими частицами и поэтому оставалась без объяснения и основная сущность явления.
Развитию гипотезы электролитической диссоциации способствовали работы И.А. Каблукова, В. Нернста, Х. Джонса и др.
Явление электролитической диссоциации наблюдается не только в водных растворах. В других растворителях, особенно обладающих высокой диэлектрической проницаемостью (в том числе и органических), происходит электролитическая диссоциация.
В настоящее время считается, что переход ионов в раствор происходит в результате образования связей между ионом и молекулами растворителя (сольватация) и, в частном случае, молекулами воды (гидратация). Объяснить это можно тем, что в среде с высокой диэлектрической проницаемостью ослабляется сила электростатического притяжения между ионами, равная, согласно закону Кулона,
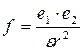 .
.
Однако этим дело не ограничивается. Если диссоциация протекает в растворителях, молекулы которых способны к образованию водородных и донорно-акцепторных связей, то этот вид взаимодействия молекул растворителя с частицами электролита может существенно влиять на ход процесса. Так, в растворителях с высокой диссоциирующей способностью (Н2О, НF) именно такое взаимодействие играет часто основную роль в процессе диссоциации. Поэтому в этиловом спирте хлористый водород диссоциирует в сильной степени, а в динитробензоле в очень слабой, хотя диэлектрические проницаемости этих растворителей различаются незначительно.
Работа разъединения ионов при растворении производится главным образом за счет их сольватации (сопровождающейся уменьшением изобарного потенциала системы).
Подобное взаимодействие с молекулами растворителя свойственно не только ионным молекулам, но и молекулам с сильной полярной связью, хотя и в более слабой степени. Это взаимодействие и приводит к диссоциации такой молекулы на ионы. Именно гидратация ионов препятствует обратному соединению ионов в молекулы.
Теплотой гидратации (или энергией гидратации) принято называть количество энергии, отвечающей процессу перевода ионов из газообразного состояния в раствор.
Большое количество энергии, выделяющейся при гидратации (сольватации) ионов, в значительной степени облегчает эндотермический сам по себе процесс диссоциации электролита и вместе с тем стабилизирует ионы, затрудняя обратный процесс их взаимного соединения.
7.2. Сильные и слабые электролиты
По способности к диссоциации электролиты разделяются на сильные и слабые. К сильным электролитам принадлежат сильные кислоты, сильные основания и большая часть солей.
Большинство сильных электролитов кристаллизуются в кристаллах с ионной решеткой, и сильными электролитами часто называют только такие вещества.
К слабым электролитам принадлежат в первую очередь слабые кислоты и слабые основания, а также некоторые соли. Сюда относятся большинство органических кислот, фенолы, амины, угольная и синильная кислота, а также такие соли, как хлорная ртуть, цианистая ртуть и др.
Процесс диссоциации слабых электролитов является обратимым. Для электролита В2А диссоциация представляется уравнением: B2A « 2B+ + A2-.
Как во всяком обратимом процессе, здесь устанавливается равновесие. Количественно его можно характеризовать константой равновесия (константой диссоциации Кд), определяемой для разбавленных растворов того же электролита В2А соотношением:
 , (7.1)
, (7.1)
где СВ+, СА2-, См – концентрации соответствующих ионов и диссоциированных молекул электролита. Соотношение (7.1) применимо к слабым электролитам в разбавленных растворах; в более концентрированных растворах или в присутствии других электролитов в значительной концентрации необходимо пользоваться вместо концентрации активностями. В этом случае соотношение (7.1) приобретает вид:
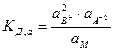 , (7.2)
, (7.2)
где а2В+, аА2- и аМ – активность ионов и недиссоциированных молекул электролита. Напомним, что активностью (точнее термодинамической активностью) данного компонента называется такая величина, которая связана с другими термодинамическими величинами так же, как в идеальных растворах с ними связана концентрация этого компонента.
Коэффициент активности g равен отношению активности к концентрации.
Константу диссоциации, определяемую через активности по уравнению (7.2), называют термодинамической константой диссоциации. Практически, однако, при отсутствии данных об активности часто приходится и для сравнительно концентрированных растворов пользоваться соотношением (7.1).
Рассчитанную таким образом КД называют иногда условной константой диссоциации, поскольку она может несколько изменяться с концентрацией.
Изменение свободной энергии Гиббса в реакциях диссоциации при их выражении через активности выглядит следующим образом:
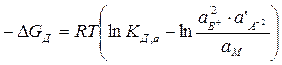 . (7.3)
. (7.3)
Оно зависит от состава раствора (концентрации данного электролита и других растворенных веществ раствора). Для стандартных условий
(a'В+ = а'А2- = a'M =1) тогда
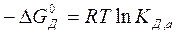 . (7.4)
. (7.4)
Для характеристики состояния слабого электролита в растворе наряду с константой диссоциации пользуются также и величиной степени диссоциации a, которая определяется отношением:
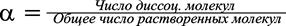 . (7.5.)
. (7.5.)
Она зависит от следующих факторов:
Ÿ от природы растворителя и растворенного вещества;
Ÿ от температуры (с ростом Т растет и a );
Ÿ от концентрации раствора (с ростом С a уменьшается);
Ÿ от наличия одноименных ионов.
в практике для характеристики силы электролита часто используются величины следующих параметров:
| Параметры | a | Кдисс | рК |
| слабый электролит | < 3% | < 10-4 | >4 |
| средней силы | 3-30% | 10-2-10-4 | 2-4 |
| сильный электролит | > 30% | >10-2 | <2 |
| рК представляет собой – lgKдисс., т.е. рК= – lg Kдисс. |
7.3. Закон разведения
В 1888 году немецкий химик В. Оствальд вывел взаимосвязь между a, КД и концентрацией электролита в растворе. Эта взаимосвязь получила название закона разведения. Так, для бинарного электролита (т.е. когда из каждой молекулы образуются два иона)
СВ+ = СА- = a С,
где С – общая концентрация электролита. Тогда
СМ = (1 - a)С,
где СМ – концентрация недиссоциированных молекул.
Подставив эти значения СВ+ ,СА- и СМ в выражение константы диссоциации, получим:
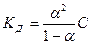 . (7.6)
. (7.6)
Для очень разбавленных электролитов a мало, и тогда 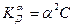 или
или
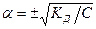 . (7.7)
. (7.7)
V – разведение, т.е. величина, обратная концентрации.
V = 1/С
и тогда
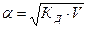 . (7.8)
. (7.8)
7.4. Сильные электролиты
Уже в работах Д.И. Менделеева, содержащих критику гипотезы электролитической диссоциации, было установлено, что во многих случаях выводы этой гипотезы неприменимы к экспериментальным данным. Опытный материал показывал, в частности, что закон действия масс неприменим к диссоциации сильных электролитов.
Дальнейшее изучение, особенно П. Дебаем и Э. Хюккелем (1923 г.), привело к следующим представлениям: 1) сильные электролиты в растворе полностью диссоциируют; 2) вокруг каждого иона образуется ионная оболочка (ионная атмосфера) за счет противоположно заряженных ионов; 3) молекулы растворителя не только находятся в пространстве между ионами, но и взаимодействуют с ними, образуя сольваты. Это отражается на свойствах как самих ионов, так и молекул растворителя. Конечно, тепловое движение частиц в той или иной мере нарушает указанную закономерность в расположении ионов. Наличие сольватационной оболочки приводит к увеличению радиуса иона и уменьшению скорости его движения, замедлению скорости химической реакции, уменьшению электропроводности раствора.
В растворе всегда экспериментально определяется меньшая концентрация вещества, чем взято для его приготовления. Поэтому различают аналитическую концентрацию (истинную) и активно проявляющуюся концентрацию, или активность: а = fc, где f – характеристика меры электростатического взаимодействия между ионами и молекулами растворителя, названная коэффициентом активности. Для бесконечно разбавленных растворов f = 1; по мере повышения концентрации f сначала уменьшается, а затем растет, преимущественно оставаясь все же меньше единицы.
Неполная диссоциация молекул, взаимное притяжение ионов, их гидратация и другие эффекты влияют на различные свойства раствора. Суммарное влияние их на любое из термодинамических свойств может быть выражено через коэффициент активности электролита в данном растворе. Поэтому коэффициент активности и активность могут быть определены путем измерения различных свойств растворов: температуры замерзания, температуры кипения, давления насыщенного пара, осмотического давления, электродвижущей силы гальванической цепи и др.
7.5. Ионная сила
При рассмотрении термодинамических свойств растворов электролитов широко используется понятие ионной силы. Она определяется как полусумма произведений из концентраций всех ионов в растворе на квадрат их заряда:
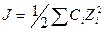 .(7.9)
.(7.9)
Для большинства биологических жидкостей ионная сила равна 0,15. Если в растворе содержатся только однозарядные ионы (т.е. электролит является одно-одновалентным), то ионная сила численно равна просто общему молярному содержанию их в растворе.
Для сильно разбавленных растворов верно следующее правило ионной силы: коэффициент активности f данного электролита в растворе зависит только от ионной силы раствора, и при одинаковом значении ее он сохраняет постоянное значение независимо от вида остальных электролитов, присутствующих в растворе:
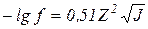 . (7.10)
. (7.10)
Уравнение (7.10) носит название предельной формы закона Дебая-Хюккеля и может применяться для описания свойств разбавленных водных растворов при ионной силе вплоть до J=0,02.
7.6. Произведение растворимости
Пусть насыщенный раствор какого-нибудь сильного электролита вида В2А3 находится в равновесии со своими кристаллами:
В2А3 кр. « 2В3+ + 3А2-.
Константа равновесия будет равна
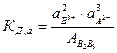 , (7.11)
, (7.11)
где аВ3+ и аА2- - активности ионов в растворе; АВ2В3 – активность электролита в осадке.
Так как АВ2В3 при каждой данной температуре постоянна, то и числитель правой части приведенного уравнения при данной температуре тоже является величиной постоянной:
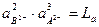 . (7.12)
. (7.12)
Постоянная La носит название произведения растворимости, если в растворе отсутствуют другие электролиты, образующие ионы, например в случае раствора AgCl, то
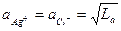 .
.
Учитывая малую растворимость хлористого серебра, можно от активностей перейти к концентрациям. Тогда
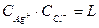
и растворимость хлористого серебра равна
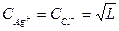 .
.
Если к насыщенному раствору хлористого серебра прибавить электролит, содержащий один общий с ним ион, то увеличение общей концентрации, например ионов Cl-, вызовет уменьшение концентрации Ag+.
Прибавление электролита, не содержащего общих ионов, может влиять на растворимость электролита лишь в той степени, в которой возрастание ионной силы раствора будет вызывать изменение коэффициентов активностей и, следовательно, самих активностей.
7.7. Электролитическая диссоциация воды
Хотя вода часто рассматривается как вещество, практически не диссоциирующее на ионы, однако в действительности в очень малой степени вода всегда диссоциирует по уравнению Н2О « Н+ + ОН-.
Правда, необходимо помнить, что водородные ионы всегда образуют в воде ионы гидроксония Н3О+. Но для простоты обычно используют в качестве обозначения ион Н+, так как это не отражается на выводах. В растворах, содержащих кислоты, образуемые ими водородные ионы влияют на положение равновесия в реакции. В случае щелочей на равновесие влияют ионы гидроксила. Для Н2О:
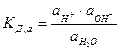 . (7.13)
. (7.13)
Для разбавленных растворов или для чистой воды вместо активности можно использовать концентрации:
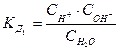 . (7.14)
. (7.14)
Степень диссоциации воды невелика, поэтому примем концентрацию ее постоянной и объединим с константой диссоциации воды в виде
Cн+ · Cон- = КВ,
где КВ – величина постоянная:
КВ = КД · CН2О . (7.15)
Эта постоянная носит название ионного произведения воды. При 25 оС ионное произведение воды КВ = 1,008 · 10-14. В чистой воде, а также в любой другой нейтральной среде Cн+ = Cон- (условие нейтральности), тогда
Cн+ = Cон-= 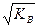 = 1,004 · 10-7 грамм-ионов в литре
= 1,004 · 10-7 грамм-ионов в литре
и, следовательно, степень диссоциации α равна
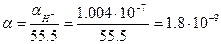 .
.
7.8. Концентрация водородных ионов
Однозначная связь между концентрациями ионов водорода и ионов гидроксила используется для характеристики кислотности и щелочности различных сред. Эти два понятия равнозначны, однако условились использовать для характеристики растворов активность водородных ионов. Практически используется не сама величина аН+, а так называемый водородный показатель рН, который определяется формулой
рН = - lgаН+, (7.16)
для разбавленных растворов
рН = - lgСН+. (7.17)
Водородным показателем называется величина, характеризующая активность (или концентрацию) водородных ионов и численно равная отрицательному десятичному логарифму этой активности (или концентрации, выраженной в грамм-ионах на литр). При 25 оС в нейтральной среде рН = 7, но с повышением температуры (поскольку реакция эндотермична) степень диссоциации повышается и наоборот:
- lgаН+ - lgаОН- = 14; - lgаН+ = рН; - lgаОН- = рОН.
рН + рОН = 14 рН = 1 рОН = 13.
Тогда для сильных кислот:
HCl ® H+ + Cl- C(HCl) = C(H+) (для разбавленных растворов)
pН = -lgCH+.
Для растворов сильных оснований:
NaOH® Na+ + OH-;
C (NaOH) = COH-; pOH = - lgCOH-;
pH = 14 – pOH = 14 + lgCOH-.
Слабые кислоты и слабые основания диссоциируют не полностью. Их способность к диссоциации определяется константой диссоциации и степенью диссоциации. В этом случае взаимосвязь между рН, рК и концентрацией слабой кислоты выглядит следующим образом:
КД и С СН3СООН « СН3СОО- + Н+
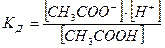 ,
,
если [CH3COOH] = CK, то:
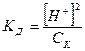 ;
; 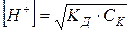
-lg [ Н+] = ½ (-lgKД – lgCк);
рН = ½ рК – ½ lgCк .
Для слабых оснований
NH4OH « NH4+ + OH-
 ;
;
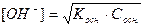
рОН = ½ рKосн –½ lgCосн; рН = 14 – ½ рKосн + ½ lgCосн .
Для слабых кислот существует следующая взаимосвязь между их концентрацией, степенью диссоциации и рН раствора:
рН = - lg (a× Ск).
В случае слабых оснований
pН = 14- рН = 14 + lga×Cосн .
7.9. Буферные растворы
Буферными растворами называются растворы с устойчивой концентрацией водородных ионов и, следовательно, с определенным значением рН, почти не зависящим от разведения и лишь слабо изменяющимся при прибавлении к раствору небольших количеств сильной кислоты или щелочи.
Такими свойствами обладают растворы, содержащие слабую кислоту или слабое основание совместно с их солью. Рассмотрим для примера раствор, содержащий уксусную кислоту и ацетат натрия. В этом случае процесс диссоциации характеризуется уравнением
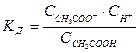 . (7.18)
. (7.18)
Присутствие ацетата практически полностью подавляет диссоциацию самой кислоты. Поэтому можно считать, что концентрация ССН3СООН практически равна исходной концентрации кислоты Ск. Концентрация ацетата равна концентрации a х Ссоли, т.е. произведению концентрации соли на степень ее диссоциации. В результате получим
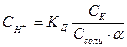 . (7.19)
. (7.19)
Для разбавленных растворов a = 1.
Тогда рН буфера будет:
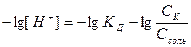 , (7.20)
, (7.20)
или
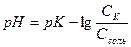 , (7.21)
, (7.21)
или
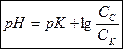 . (7.22)
. (7.22)
Для основных буферов:
 (7.23)
(7.23)
Величина рН – буферных растворов зависит:
Ÿ от показателя константы диссоциации слабой кислоты или слабого основания;
Ÿ от соотношения компонентов буферного раствора.
DрН = рК + 1 – зона буферного действия раствора.
В этом интервале значений рН наиболее четко поддерживается активная кислотность среды.
7.10. Механизм действия буферных растворов
При рассмотрении механизма действия буферов необходимо ответить на два вопроса:
Ÿ Почему рН буферного раствора не меняется при разбавлении?
Ÿ Почему рН буферного раствора не меняется при добавлении небольших количеств сильных кислот или сильных оснований?
При разведении константы диссоциации слабых кислот или оснований не меняются. Отношение концентраций кислоты и соли также остается постоянным. В результате рН сохраняется.
При добавлении сильной кислоты к буферу Н+-ионы реагируют с солевой компонентой и превращаются в недиссоциированную форму. Концентрация Н+ ионов уменьшается, концентрация слабой кислоты увеличивается, степень диссоциации уменьшается, а рН раствора практически не меняется.
При добавлении сильной щелочи ОН-–ионы реагируют с кислотой. Сильное основание заменяется на эквивалентное количество слабого электролита воды. Причины неизменения рН заключаются в превращении сильного основания в слабый электролит.
7.11. Буферная емкость
Буферной емкостью называется количество моль-эквивалентов сильной кислоты или сильного основания, которые можно добавить к 1 л буферного раствора, чтобы рН изменилась на одну единицу.
Буферная система крови. В норме рН крови находится в пределах 7,4 + 0,04. Хотя какой-то вклад в буферные свойства вносит гемоглобин и другие белки, а также фосфаты, все же главным компонентом буферной системы крови служит пара бикарбонат натрия/угольная кислота.
Лекция 8. Основные понятия химической кинетики
8.1. Химическая реакция
Химической реакцией можно считать любое изменение вещества, при котором образуется или разрывается химическая связь между атомами. Химическая реакция характеризуется механизмом ее протекания и глубиной протекания.
8.2. Механизм химической реакции
Химические реакции, как правило, не происходят путем непосредственного взаимодействия исходных молекул с прямым переходом их в молекулы продуктов реакции. В большинстве случаев реакции протекают в несколько стадий. Например, окисление ионов двухвалентного железа в кислом растворе молекулярным кислородом состоит из ряда стадий:
Fe2+ + O2 ® Fe3+ + O2-
O2- + H+ ® HO2·
Fe2+ + HO2· ® Fe3+ + HO2-
HO2- + H+ ® H2O2
H2O2 + Fe2+® Fe3+ + OH- + OH·
Fe2+ + OH· ® Fe3+ + OH-
OH- + H+ ® H2O.
Общее стехиометрическое уравнение реакции:
4Fe2+ + 4H+ + O2 ® 4Fe3+ + 2H2O.
Этот сложный путь оказывается, тем не менее, неизмеримо более выгодным, так как ни на одном из семи этапов не требуется встречи более чем двух частиц и ни на одном из этапов не требуется соударения одноименно заряженных частиц.
Совокупность стадий, из которых складывается химическая реакция, носит название механизма химической реакции.
8.3. Исходные, конечные и промежуточные вещества
Вещества, вступающие в процесс химического превращения, называются исходными. Вещества, образующиеся в процессе химического превращения и не претерпевающие в ходе этого процесса дальнейших химических изменений, называются продуктами реакции. Вещества, образующиеся в одних стадиях процесса химического превращения и расходующиеся в других стадиях этого же процесса, называют промежуточными веществами.
8.4. Глубина превращения реакции
Глубина характеризует степень превращения исходных веществ в конечные продукты реакции. Проведенные измерения привели химиков к убеждению, что, во-первых, все мыслимые реакции в какой-то степени происходят, и, во-вторых, не существует реакций, идущих полностью до конца. Однако часто удобнее говорить, что одни реакции совсем не идут, другие идут в ограниченной степени, а третьи потребляют исходные вещества полностью.
8.5. Гомогенные и гетерогенные реакции
Химическая реакция, протекающая в пределах одной фазы, называется гомогенной.
Химическая реакция, протекающая на границах раздела фаз, называется гетерогенной.
Примером гомогенной может служить любая реакция в растворе. Примером гетерогенной может служить любая из реакций, идущих на поверхности твердого катализатора (гетерогенная каталитическая реакция).
8.6. Скорость химической реакции
Важнейшей количественной характеристикой процесса химического превращения является скорость процесса. Понятие скорости характеризует количество вещества, вступающего в реакцию в единицу времени. Это определение, однако, не совсем однозначно, так как в реакции принимают участие несколько веществ в качестве исходных, промежуточных и в качестве продуктов реакции. Поэтому строго можно говорить не о скорости химического процесса вообще, а о скорости по некоторому компоненту. Изменение количества этого компонента принято выражать в числе молей n. Таким образом, для гомофазного химического процесса, идущего при постоянном объеме, скоростью процесса по некоторому веществу называется изменение концентрации этого вещества в единицу времени. Пусть концентрация одного из реагирующих веществ в момент времени t1 равна С1, а в момент времени t2 равна С2. Тогда средняя скорость реакции (`V ) за промежуток времени t2 – t1 равна
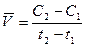 . (8.1)
. (8.1)
Поскольку концентрация вещества (исходного) в процессе реакции убывает, то C2 < C1 и разность C2 – C1 имеет отрицательный знак, т.е. C2 – C1 = -DС. Отсюда средняя скорость
 . (8.2)
. (8.2)
Переходя к бесконечно малым изменениям, можно отношение - 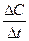 заменить на -
заменить на - 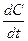 . В результате производная от концентрации по времени характеризует мгновенную (истинную) скорость химической реакции:
. В результате производная от концентрации по времени характеризует мгновенную (истинную) скорость химической реакции:
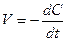 . (8.3)
. (8.3)
Скорость химической реакции всегда является величиной положительной, отношение же dC/dt может иметь и положительное, и отрицательное значение в зависимости от того, представляет С концентрацию одного из исходных веществ или одного из продуктов реакции. В первом случае dC/dt< 0, но так как скорость должна быть положительной, перед производной ставят минус; во втором случае dС/dt> 0, и чтобы скорость реакции имела положительное значение, берут производную со знаком плюс. В общем случае кинетическое уравнение имеет вид
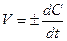 . (8.4)
. (8.4)
Однако необходимо учитывать, что измеренные по разным веществам скорости не равны, а пропорциональны одна другой. Например, в реакции синтеза аммиака
N2 + 3H2 « 2HN3
на каждый исчезающий моль N2 расходуется 3 моля H2 и образуется 2 моля аммиака. Соответствующие скорости реакции соотносятся как 1: 3: 2.
Скорость реакции имеет размерность [концентр] × [время]-1. В химической кинетике концентрацию чаще всего выражают в моль/л, а время – в секундах. Отсюда скорость химической реакции выражается в моль× л-1 ×с-1.
8.7. Измерение скорости реакции
В химической кинетике широко используется графический метод изображения функциональных зависимостей. Кривая, изображающая зависимость концентрации какого-либо вещества от времени в ходе процесса химического превращения, носит название кинетической кривой. Крутизна кинетической кривой в каждый момент времени характеризует истинную скорость реакции в этот момент времени, так как наклон касательной в точке численно равен скорости: V = - dc/dt = tga (рис. 8.1):
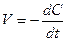 . (8.5)
. (8.5)
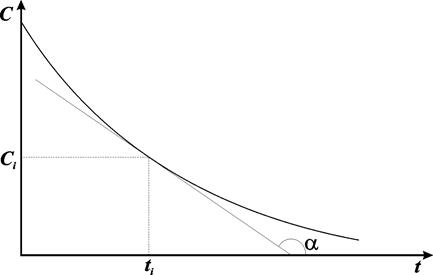
Рис. 8.1. Кривая, изображающая зависимость концентрации какого-либо вещества от времени в ходе процесса химического превращения, носит название кинетической кривой
Часто под кинетическими кривыми понимают и другие зависимости изменения какого-либо изменяющегося параметра в ходе химической реакции (изменение рН, электропроводности, показателя преломления, оптической плотности и т.д.). Однако рассчитывать скорость накопления или расходования какого-либо из компонентов реакции, исходя из такой кривой, можно лишь в том случае, если существует и известна однозначная зависимость, связывающая концентрацию этого компонента с измеряемым свойством системы.
8.8. Порядок реакции и константа скорости реакции
Скорость химической реакции зависит от целого ряда факторов. При заданных внешних условиях (температура, давление, среда, в которой проходит процесс) скорость является функцией концентрации реагирующих веществ. Зависимость скорости реакции от концентрации реагирующих веществ описывается основным постулатом химической кинетики: скорость реакции в каждый момент времени пропорциональна произведению концентраций реагирующих веществ, имеющихся в данный момент времени, возведенных в некоторые степени. Этот постулат вытекает из физически очевидного предположения о том, что реагируют те молекулы, которые сталкиваются. Известно, что число столкновений зависит от концентрации молекул, поэтому и скорость химической реакции должна определяться теми же факторами. Итак, для реакции А + В ® С + Д можно записать V = k[A]n1× Bn1 , где величины n принято называть порядком реакцию по веществу А и В и т.д. Сумму порядков реакции по всем реагирующим веществам называют порядком реакции.
Следует подчеркнуть, что величины n1 и n2 определяются только экспериментальным путем, так как для подавляющего большинства реакций порядки реакции по веществу не равнозначны стехиометрическим коэффициентам.
Порядок реакции – величина формальная. Он может быть положительным или отрицательным, целым или дробным, а также нулевым числом. Как было уже указано, порядок реакции определяется опытным путем, и его нельзя предсказать заранее, даже для формально простых реакций. Например, скорость реакции H2 + J2 = 2HJ согласно опытным данным может быть записана следующим образом: V = k [H2] [J2], где порядок реакции по водороду и йоду равен единице, а порядок реакции в целом равен 1 + 1 = 2. В этом случае стехиометрическое уравнение правильно изображает элементарный акт реакции.
Однако в большинстве сложных реакций, протекающих через несколько стадий, когда общее стехиометрическое уравнение не отражает действительного хода реакции, показатели степени в уравнении скорости реакции не будут соответствовать стехиометрическим коэффициентам, т.е. закон действия масс для химических реакций выполняется лишь в некоторых частных случаях.
Можно утверждать, что стехиометрическое уравнение реакции, устанавливающее пропорции реагентов и продуктов, не определяет механизма протекания этой реакции во времени. Это является причиной, по которой экспериментально найденный порядок не всегда согласуется с уравнением, описывающим реакцию.
Множитель k в уравнении показывает, с какой скоростью идет химический процесс при концентрациях реагирующих веществ, равных 1 моль/л, и его называют константой скорости химического процесса. Он не зависит от концентрации и характеризует лишь влияние природы реагирующих веществ на скорость их взаимодействия друг с другом, т.е. константа скорости реакции является мерой реакционной способности молекул.
Размерность констант скорости реакции различного порядка легко получить из выражения для скорости реакции.
Нулевой порядок
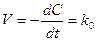 ; k0 = [C][t]-1. (8.6)
; k0 = [C][t]-1. (8.6)
Первый порядок
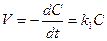 ; k1 = [t]-1. (8.7)
; k1 = [t]-1. (8.7)
Второй порядок
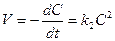 ; k2 = [C-1][t]-1. (8.8)
; k2 = [C-1][t]-1. (8.8)
Константы скорости реакций разных порядков имеют разные размерности и, поэтому их сравнение не имеет смысла. Хотя скорость некоторых химических реакций описывается кинетическим уравнением третьего порядка, однако это еще не значит, что они являются тримолекулярными. Все же укажем:
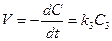 ; k3 = [c]-2[t]-1 . (8.9)
; k3 = [c]-2[t]-1 . (8.9)
8.9. Молекулярность реакции
Молекулярность реакции определяется числом молекул, одновременно сталкивающихся и приводящих к химическим превращениям. Взаимодействие подобного рода носит название элементарного акта химического превращения, т.е. молекулярность реакции, в отличие от порядка реакции, имеет вполне определенный физический смысл. Например, реакция J2 = 2J – мономолекулярная, так как в ее основе лежит распад исходного вещества; реакция H2 + J2 = 2HJ – бимолекулярная; реакция 2NO + H2 = N2O + H2O является примером тримолекулярной реакции. Молекулярность более высокого порядка не встречается, так как одновременное столкновение четырех частиц почти невероятно.
В случае сложных реакций, протекающих в несколько стадий, нет смысла говорить о молекулярности реакции в целом, поскольку это понятие имеет отношение применимо только к отдельным стадиям.
Различие между молекулярностью и порядком реакции можно свести к следующему:
1) молекулярность реакции имеет вполне определенный физический смысл, а порядок реакции – величина формальная;
2) порядок реакции может принимать любые значения: целые, дробные и даже отрицательные, численные значения молекулярности ограничены лишь тремя цифрами – 1,2,3;
3) порядок реакции можно использовать для характеристики любых реакций (как сложных, так и простых), понятие «молекулярность» применимо только к элементарным актам химических превращений.
8.10. Количественные соотношения между скоростью
реакции и концентрацией реагента
В реакции первого порядка скорость реакции пропорциональна концентрации одного реагента. Для нее
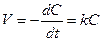 . (8.10)
. (8.10)
Для нахождения С в каждый момент времени t это уравнение необходимо проинтегрировать:
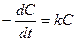 ;
; 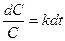 , (8.11)
, (8.11)
после интегрирования
ln c = - kt + const. (8.12)
Значение const находим из начальных условий, из которых следует, что С0 – начальная концентрация в момент времени t = 0. Определим постоянную как ln С0. Отсюда
ln С = - kt + lnC0; ln C – ln C0 = - kt; ln C/C0 = -kt (8.13)
или
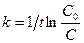 . (8.14)
. (8.14)
Заменив натуральные логарифмы на десятичные, получим:
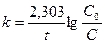 . (8.15)
. (8.15)
Особенность реакции первого порядка заключается в том, что равным промежуткам времени отвечают равные доли С0/С прореагировавшего вещества (рис. 8.2). Время t, нужное для того, чтобы прореагировала половина С0, называется периодом полупревращения: подставляя в уравнение t1/2 = t и С = С0/2, получим:
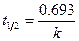 , (8.16)
, (8.16)
т.е. для реакции первого порядка период полупревращения t1/2 не зависит от начальной концентрации и служит характеристикой скорости таких реакций.
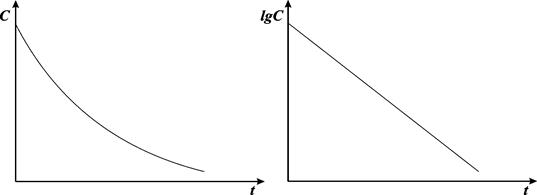
Рис. 8.2. Зависимость lgС от времени для реакции первого порядка
8.11. Реакция второго порядка
Выражение скорости для реакции второго порядка имеет вид:
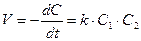 (8.17)
(8.17)
или
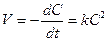 . (8.18)
. (8.18)
Разделяя переменные, получим:
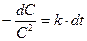 ; (8.19)
; (8.19)
после интегрирования:
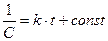 . (8.20)
. (8.20)
При C0 и t = 0 определяем постоянную интегрирования, равную 1/С0. Отсюда
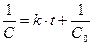 или
или 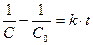 ; (8.21)
; (8.21)
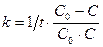 . (8.22)
. (8.22)
Период полупревращения для реакции второго порядка не остается постоянным, а обратно пропорционален начальной концентрации (рис. 8.3):
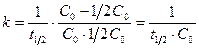 . (8.23)
. (8.23)
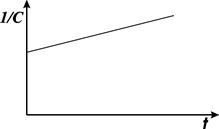
Рис. 8.3. Зависимость 1/C от времени для реакции второго порядка
8.12. Уравнение скорости реакции третьего порядка
Хотя скорость некоторых химических реакций описывается кинетическим уравнением третьего порядка, это еще не значит, что они действительно тримолекулярные. Однако оно удобно для вывода кинетического уравнения:
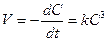 . (8.24)
. (8.24)
После интегрирования получим:
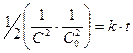 или
или 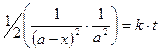 , (8.25)
, (8.25)
если а – исходная концентрация, (а - х) – количество вещества, оставшегося ко времени t. Если реакция протекает по уравнению: 2А + В ® продукты и если [B] не равна [A], то интегрирование выражения для скорости реакции третьего порядка значительно усложняется.
8.13. Уравнение скорости реакции нулевого порядка
Если в уравнении скорости отсутствуют члены, содержащие концентрацию реагирующих веществ, то скорость такой реакции выражается уравнением нулевого порядка
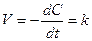 . (8.26)
. (8.26)
Реакция нулевого порядка представляет особый интерес в каталитических процессах, когда катализатор, взятый в определенном количестве, может служить фактором, лимитирующим скорость реакции. Такая ситуация встречается в ферментативной кинетике.
8.14. Определение порядка реакции
Порядок реакции играет существенную роль при изучении и раскрытии механизма реакции. Он в значительной степени зависит от механизма реакции. Порядок реакции определяется опытным путем, и его нельзя предсказать заранее, даже для реакций формально похожих.
а) Для определения порядка реакции часто используют способ подстановки. Он заключается в выборе уравнения кинетики реакции (нулевого, первого, второго порядков) при подстановке в которое экспериментальных данных получается постоянное значение константы скорости реакции.
б) Существует и графический способ определения порядка реакции. Например, для реакции нулевого порядка скорость реакции не зависит от концентрации. Для реакции первого порядка прямолинейной является зависимость lnC от времени. Для реакции второго порядка линейной будет зависимость 1/С от времени.
в) Используется также определение зависимости от концентрации константы полупревращения и т.д.
8.15. Теоретические основы химической кинетики
В основе современной химической кинетики лежат две теории: теория активных соударений и теория активного комплекса.
Дата добавления: 2016-02-09; просмотров: 1584;
