Лекция 5. Химические реакции как открытые в термодинамическом смысле системы. Направление протекания химических реакций. Равновесные химические реакции
5.1. Понятие о химическом потенциале
Химическую реакцию можно рассматривать с точки зрения изменения в системе количеств продуктов реакции и исходных веществ.
Изменение энергии системы с увеличением числа молей данного вещества на единицу времени при неизменных прочих параметрах системы можно рассмотреть на следующей простой модели.
В сосуде при постоянном давлении и температуре находятся три газа: азот n(N2), кислород n(О2) и водород n(H2) в одинаковых количествах:
n(N2) = n(O2) = n(H2).
Из сосуда можно вывести или (ввести) один моль какого-либо газа, например кислорода. Очевидно, для этого нужно затратить энергию:
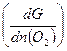 при Р и Т, n(N2) и n(H2) = const. (5.1)
при Р и Т, n(N2) и n(H2) = const. (5.1)
Изменение энергии Гиббса системы в этом случае может быть записано как:
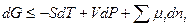 , (5.2)
, (5.2)
где mi – коэффициент пропорциональности между изменением энергии и количества i-го компонента.
Определим изменение энергии Гиббса системы от изменения давления. Учтем, что 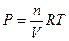 , поэтому это фактически равнозначно изменению энергии Гиббса, связанному с изменением концентрации вещества в системе:
, поэтому это фактически равнозначно изменению энергии Гиббса, связанному с изменением концентрации вещества в системе:
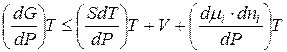 . (5.3)
. (5.3)
Так как изменение энергии системы рассматривается при постоянной Т, следовательно -SDТ = 0, а так как dn = 1 (количество газа в системе изменяется на 1 моль), то
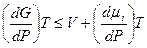 . (5.4)
. (5.4)
Так как V = const, следовательно, изменение mi в системе пропорционально изменению энергии Гиббса системы. Из этого следует, что коэффициент пропорциональности mi характеризует изменение энергии Гиббса системы, связанной с изменением количества вещества.
При достижении системой равновесия dG = 0 и, следовательно,
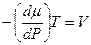 . (5.5)
. (5.5)
Для одного моля газа (идеального) V = RT/Р.
Подставим это выражение в уравнение (5.5) и проведем интегрирование. Получим:
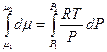 , (5.6)
, (5.6)
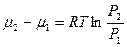 , (5.7)
, (5.7)
где m1 и m2 – химический потенциал чистого газа при давлениях Р1 и Р2 (соответственно) и температуре Т соответственно:
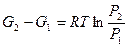 . (5.8)
. (5.8)
Удобно выбрать Р1, равным 1 атм, тогда m1 можно обозначить как m0, т.е. химический потенциал одного моля чистого газа при 1 атм и температуре Т (стандартный химический потенциал), тогда приведенные уравнения могут быть записаны так:
m = m0 + RT lnP, (5.9)
G = G0 +RT lnP. (5.10)
С другой стороны, можно рассматривать любой вид энергии как произведение двух величин: фактора интенсивности и фактора емкости.
| Типы энергии | Интенсивная величина | Экстенсивная величина |
| Работа в гравитационном поле | h (высота) | m (масса) |
| Поверхностная энергия | s (поверхностное натяжение) | S (площадь) |
| Электрическая работа | U (напряжение) | q (заряд) |
| Работа расширения газа | Р (давление) | V (объем) |
| Механическая энергия (работа) | F (сила) | l (расстояние, длина) |
| Химическая работа | Химический потенциал | n (кол-во вещества) |
Интенсивная величина (фактор интенсивности), показывающая изменение энергии системы с изменением массы, носит название химического потенциала.
5.2. Экзергонические и эндергонические реакции
Величина DG служит мерой способности системы производить работу. Она позволяет решить вопрос, может ли реакция протекать самопроизвольно.
Реакциия протекает самопроизвольно только в том случае, если происходит уменьшение энергии Гиббса системы. Такие реакции называют экзергоническими.
Если же энергия Гиббса системы возрастает, то для осуществления реакции необходимо затратить работу. Такие реакции называют эндергоническими.
В живых организмах реакцию, которая в данных условиях не является самопроизвольной, поскольку протекание ее связано с увеличением «свободной энергии», можно осуществить путем сопряжения ее с другой реакцией, характеризующейся достаточно большой отрицательной величиной изменения энергии Гиббса. Условием такого сопряжения будет наличие интермедиата, т.е. общего для обеих реакций вещества.
Пример:
1. А + В « С + Д; DG1o > 0.
2. Д + К « М + Г; DG2o < 0.
3. Ф + В + К « С + М + Г; DG3 < 0.
Для живых организмов можно привести много примеров сопряженных реакций. Особенно большое значение имеют реакции гидролиза таких соединений, как аденозинтрифосфат (АТФ), аденозиндифосфат (АДФ), аргининфосфат, креатинфосфат, характеризующихся величинами изменения энергии Гиббса от –29,99 до –550,21 кДж/моль. Отметим, что широко распространенный термин «богатая энергией связь» в этом случае в химическом понимании неточен, поскольку в данной интерпретации он относится не к энергии связи в химическом понимании, а к стандартной энергии Гиббса, характеризующей гидролиз фосфатного соединения.
Энергия связи в химическом понимании – это энергия, которая должна быть затрачена для разрыва связи в молекуле с образованием нейтральных атомов или радикалов.
Концепция, согласно которой энергия локализована в богатой фосфатной связи и освобождается при ее расщеплении, получила значительное распространение. Однако энергия разрыва связи и, следовательно, представление о том, что процесс расщепления связи поставляет энергию и что энергия запасается в связи, не имеет физического смысла.
Большая величина стандартной энергии Гиббса гидролиза фосфатных соединений связана с тремя факторами. Первый – более высокая термодинамическая стабильность продуктов гидролиза по сравнению с исходными соединениями. Второй – в исходных соединениях имеются близко расположенные отрицательно заряженные кислотные группы и часть энергии, освобождаемой при гидролизе, связана с электростатическим отталкиванием этих групп в исходном состоянии. Третий – это вклад энергии ионизации групп, образующихся при гидролизе. Таким образом, совокупность протекающих при гидролизе процессов определяет общий, конечный эффект.
5.3. Взаимосвязь энтальпийного и энтропийного
факторов в качестве критерия самопроизвольного
протекания химической реакции
Из уравнения
DGo = DНo – ТDSo (5.11)
видно, что знак DG зависит от двух факторов: DH – энтальпийного фактора, характеризующего стремление системы к минимуму полной энергии системы и DS – энтропийного фактора, характеризующего стремление системы к переходу в более беспорядочное состояние. Значит DG является интегральным показателем, отражающим взаимосвязь энтальпийного и энтропийного факторов. Рассмотрим несколько возможных вариантов:
1) DНo< 0; DS > 0; DG< 0 – это относится к экзотермическим реакциям, идущим с увеличением энтропии. Такие реакции протекают самопроизвольно в стандартных условиях.
2) DНo > 0; DS < 0; DG > 0 –эндотермические реакции, идущие с уменьшением энтропии. Такие реакции возможны в сопряжении с другими процессами; 6Н2О + 6СО2 ® С6Н12О6.
3) Другие возможные варианты:
DН < 0; DS < 0;
|DН| > |TDS|; DGo< 0;
|DН| < |TDS|; DGo > 0;
|DН| = |TDS|; DGo = 0.
5.4. Понятие о равновесии химической реакции.
Обратимые и необратимые реакции
Учение о химическом равновесии является одним из важнейших разделов физической химии. Начало ему положено работами французского ученого К. Бертолле (1799 г.) и в наиболее общем виде развито норвежскими учеными К. Гульдбергом и П. Вааге (1867 г.), установившими закон действующих масс.
Химическое равновесие устанавливается в системах, в которых протекают обратимые химические реакции.
Обратимой химической реакцией называют такую реакцию, продукты которой, взаимодействуя между собой в тех же условиях, при которых они получены, образуют некоторые количества исходных веществ.
С эмпирической точки зрения химическим равновесием называют состояние обратимой химической реакции, при котором концентрации реагирующих веществ в данных условиях не меняются со временем.
Примером здесь являются реакция получения йодоводорода из водорода и йода
Н2 (Г) + J2 (Г) « 2НJ (Г),
и реакция этерификации
С2Н5ОН (Ж) + СН3СООН (Ж) « С2Н5СООСН3 (Ж) + Н2О (Ж),
так как образующиеся продукты реакции (йодоводород и уксусно-этиловый эфир) способны в тех же условиях, при которых они получены, образовывать исходные вещества.
Необратимой химической реакцией называют такую реакцию, продукты которой не взаимодействуют друг с другом при тех же условиях, в которых они получены, с образованием химических веществ.
Пример – реакция разложения бертолетовой соли на кислород и хлорид калия:
2KClO3 (Т) ® 2KCl (Т) + 3О2 (Г).
Образующиеся в этих случаях продукты реакции не способны взаимодействовать друг с другом с образованием исходных веществ в условиях их получения.
Понятия об обратимых и необратимых химических реакциях не следует путать с понятиями об обратимых и необратимых процессах (в том числе и химических реакций) в термодинамическом смысле.
5.5. Уравнение изотермы химической реакции
и вывод закона действующих масс
Рассмотрим обратимую химическую реакцию, протекающую между газообразными веществами в изобарно-изотермических условиях в соответствии с уравнением аА + вВ « mM + nN.
Изменение количеств реагирующих веществ в процессе протекания химической реакции до достижения равновесия можно рассматривать как изъятие из системы веществ или добавление продуктов реакции.
Изменение химических потенциалов каждого компонента в этом случае выразится следующим образом:
mА = amоА + a RTln CA,
mB = bmоB + b RTln CB,
mM = mmоM + mRTln CM,
mN = nmоN + nRTln CN.
Общее изменение химического потенциала в системе при протекании химической реакции можно выразить как
Dm = Snim(прод) - Snim(исх) (5.12)
или
Dm = mmоM + RT ln 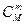 + nmоN + RTln
+ nmоN + RTln 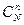 - amоА - RTln
- amоА - RTln 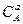 - bmоB – RTln
- bmоB – RTln 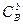 .
.
Обозначим mmоM + nmоN - amоА- bmоB через Dmо и, преобразовав сумму логарифмов в логарифм дроби, получим:
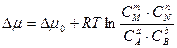 . (5.13)
. (5.13)
Необходимо отметить, что через С обозначены исходные концентрации участников реакции.
При установлении химического равновесия изменение химического потенциала равно нулю. В соответствии с этим уравнение (5.13) примет вид:
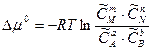 , (5.14)
, (5.14)
при этом через 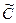 обозначены концентрации участников реакции при достижении системой равновесия.
обозначены концентрации участников реакции при достижении системой равновесия.
Из уравнения (5.14) следует, что
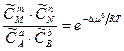
при постоянной температуре – величина постоянная, так как Dmо есть величина постоянная для данной реакции и, следовательно,
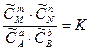 . (5.15)
. (5.15)
Уравнение (5.15) является математическим выражением закона действующих масс, установленного в 1867 году норвежскими учеными К. Гульдбергом и П. Вааге, согласно которому отношение произведения равновесных концентраций продуктов реакции, возведенных в степени, показатели которых равны их стехиометрическим коэффициентам, к произведению равновесных концентраций исходных веществ в степенях, показатели которых равны их стехиометрическим коэффициентам, для данной обратимой реакции есть величина постоянная при данной температуре.
Эта величина получила название константы химического равновесия.
Принимая во внимание, что изменение энергии Гиббса системы DG=SmiDn, аналогичными рассуждениями можно показать, что
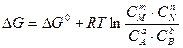 . (5.16)
. (5.16)
Приведенное уравнение называют уравнением изотермы химической реакции, или уравнением изотермы Вант-Гоффа. Оно позволяет производить расчет изменения энергии Гиббса при протекании химической реакции. Условия достижения системой состояния равновесия определяются DG= 0, следовательно, можно записать для состояния равновесия:
DGо = -RTlnK. (5.17)
Подставив значение DGо в уравнение (5.16), получим:
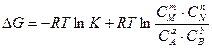 . (5.18)
. (5.18)
Критерием самопроизвольного протекания химического процесса является уменьшение свободной энергии (энергии Гиббса) системы, т.е. DG <0.
Анализ уравнения (5.18) показывает, что это возможно в том случае, если
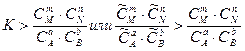 .
.
В этом случае система, находящаяся в неравновесном состоянии, будет стремиться к состоянию равновесия, и при этом концентрация исходных веществ будет уменьшаться, а продуктов – увеличиваться, т.е. реакция будет протекать в прямом направлении. Рассмотрим условие, при котором
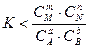 (т.е. DG >0).
(т.е. DG >0).
Если DG > 0, то, следовательно, самопроизвольное протекание прямой реакции невозможно. Однако при этом протекание обратной реакции должно сопровождаться уменьшением энергии Гиббса, т.е. DG<0 и, следовательно, при условии 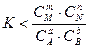 самопроизвольно будет протекать обратная реакция.
самопроизвольно будет протекать обратная реакция.
Уравнение (5.17) можно использовать для расчета констант химического равновесия. Для этого необходимо вычислить изменение стандартной энергии Гиббса, происходящее в результате протекания реакции при постоянных Р и Т. Их расчет приводит по уравнению
DGo = Sni DGo(пр)- Sni DGo(исх). (5.19)
Зная DGo, вычисляют константу химического равновесия:
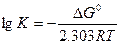 . (5.20)
. (5.20)
5.6. Зависимость константы химического равновесия
от температуры
Для установления зависимости константы химического равновесия от температуры рассмотрим состояние равновесия химической реакции при произвольных Т1 и Т2. Предположим, что DНo и DSo в интервале температур от Т1 до Т2 остаются постоянными, тогда константы химического равновесия при Т1 и Т2 могут быть выражены:
DG1o = - RT lnK1 DG1o = DНo –T1DSo;
DG2o = - RT lnK2 и соответственно DG2o = DНo –T2DSo.
Решим систему приведенных уравнений относительно константы равновесия химической реакции:
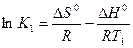 (1),
(1),
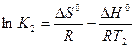 (2).
(2).
Вычтем из первого уравнения второе:
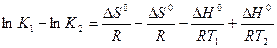
или
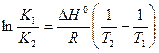 (5.21)
(5.21)
(интегральная форма уравнения изобары).
Полученная зависимость позволяет определить смещение состояния равновесия при изменении температуры. Предположим, что DHo>0 – эндотермическая реакция, тогда при увеличении температуры (Т2>Т1) величина ln K1/K2< 0, что выполняется при условии K1< K2 (K1/K2< 1), т.е. равновесие химической реакции смещается в сторону образования продуктов реакции. Уменьшение температуры (Т2<Т1) приведет соответственно к смещению равновесия в сторону образования исходных веществ.
При условии, что реакция – экзотермическая (DHo < 0), повышение температуры (Т2 >Т1) определяет 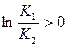 , из чего следует, что K1>K2 (K1/K2>1), т.е. равновесие экзотермической реакции при повышении температуры смещается в сторону образования исходных участников реакции, и соответственно, понижение температуры проведения реакции – в сторону продуктов.
, из чего следует, что K1>K2 (K1/K2>1), т.е. равновесие экзотермической реакции при повышении температуры смещается в сторону образования исходных участников реакции, и соответственно, понижение температуры проведения реакции – в сторону продуктов.
Часто для анализа направления смещения равновесия химической реакции при изменении температуры удобно пользоваться дифференциальной формой уравнения изобары 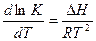 .
.
1) DH< 0; 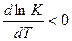
 dT > 0 – для экзотермической реакции увеличение температуры приводит к уменьшению константы химического равновесия, если dT < 0 уменьшение t приводит к росту K (константы химического равновесия);
dT > 0 – для экзотермической реакции увеличение температуры приводит к уменьшению константы химического равновесия, если dT < 0 уменьшение t приводит к росту K (константы химического равновесия);
2) DH > 0; dT > 0 – для эндотермической реакции увеличение температуры ведет к увеличению K;
3) DТ< 0 – для экзотермической реакции уменьшение t ведет к уменьшению К химического равновесия.
Проведенный анализ зависимостей константы химического равновесия показывает, что смещение системы из состояния равновесия путем внешнего воздействия (изменение температуры, давления, концентрации) приводит к увеличению энергии Гиббса, и самопроизвольно могут протекать те процессы, которые противодействуют возрастанию DG, т.е. процессы, связанные с уменьшением энергии Гиббса, что является термодинамическим обоснованием принципа Ле-Шателье.
Принцип смещения равновесия химической реакции, сформулированный Ле-Шателье, а затем Брауном, можно выразить следующим образом: если на систему, находящуюся в устойчивом равновесии, подействовать извне, изменив какое-нибудь из условий, определяющих равновесие, то в системе усилится то из направлений процесса, течение которого ослабляет влияние произведенного воздействия, и положение сместится в том же направлении.
Дата добавления: 2016-02-09; просмотров: 1797;
