Расчет изменения энтропии сложного процесса
Изменение энтропии сложного процесса, состоящего из нескольких стадий, равняется сумме изменений энтропий каждой отдельной стадии этого процесса:
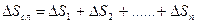. (4.8)
Например, изменение энтропии при обратимом превращении 10,0 г льда, находящегося при -10 °С, в пар при 120 °С, если
С(Н2О, ТВ) = 2,03 Дж г-1 К-1; DНпл. льда = 331,89 Дж г-1;
С(Н2О, Ж) = 4,18 Дж г-1 К-1; DНисп. Н2О = 2253,4 Дж г-1.
С(Н2О, Г) = 1,93 Дж г-1 К-1;
Вычисляют следующим образом.
Данный процесс представим из пяти стадий:
1. Нагревание льда от -10 °С до 0 °С, DS1.
2. Плавление льда, DS2.
3. Нагревание жидкой воды от 0°С до 100 °С, DS3.
4. Испарение воды, DS4.
5. Нагревание пара от 100 °С до 120 °С, DS5.
Изменение энтропии в 1, 3, 5 стадиях рассчитывают по уравнению
.
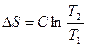В стадиях 2, 4 – по уравнению 
.
Общее изменение энтропии составит: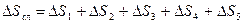 
.
4.4. Расчет изменения энтропии
при протекании химического процесса
Изменение энтропии химического процесса равно алгебраической сумме стандартных энтропий участников реакции с учетом их стехиометрических коэффициентов, причем энтропии продуктов реакции берутся со знаком плюс, а энтропия исходных веществ – со знаком минус.
Для реакции, протекающей по уравнению aА + bB ® mM + nN
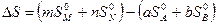. (4.9)
В общем виде:
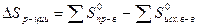(4.10)
(с учетом стехиометрических коэффициентов).
4.5. Критерии направления протекания процессов
и достижения равновесных состояний
в открытых и закрытых системах.
Понятие об энергии Гиббса
По изменению энтропии можно судить о направлении и пределах протекания процессов только в изолированных системах. В случае закрытых и открытых систем необходимо также учитывать изменение энтропии окружающей среды. Решение последней задачи сложно или невозможно. Поэтому в термодинамике для изучения открытых или закрытых систем используют другие термодинамические функции, так называемые термодинамические потенциалы, изменение которых позволяет определить направление процессов и пределы их протекания без учета изменений в окружающей среде. В частности, к термодинамическим потенциалам относится функция состояния, называемая энергией Гиббса, которую обозначают через G.
Понятие об энергии Гиббса было введено на основе объединенного уравнения первого и второго начал термодинамики. Это уравнение может быть выведено следующим образом. Из первого начала термодинамики следует:
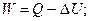
; (4.11)
из второго начала термодинамики для обратимого процесса получаем:
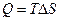. (4.12)
Для необратимого процесса:
< 
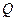. (4.13)
Подставляя значение 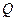из уравнения (4.12) и уравнений (4.13) в (4.11), находим:
для обратимого процесса
; (4.14)
для необратимого процесса
< 
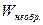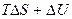. (4.15)
Уравнение (4.14) называют объединенным уравнением первого и второго начал термодинамики для обратимых процессов. Так как внутренняя энергия и энтропияявляются функциями состояния, то их изменения не зависят от того, как протекает данный процесс, обратимо или необратимо, следовательно:
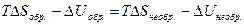и 
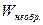> , (4.16)
т.е. работа, совершаемая при обратимом процессе, больше работы, производимой системой при необратимом процессе при условии, что начальное и конечное состояния системы одинаковы в обоих случаях.
Имея в виду, что работа, производимая системой при обратимом процессе, является максимальной для данного изменения состояния системы, преобразуем уравнение (4.14):
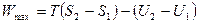. (4.17)
группируя величины с одинаковыми индексами, получим:
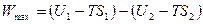, (4.18)
так как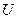 
и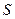 
– функции состояния, то величина ( 
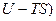должна быть также функцией состояния.
Если система кроме полезной работы совершает работу против силы внешнего давления (Р = const), то для обратимого процесса
(4.19)
или
,
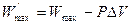где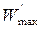 
– максимальная полезная работа, совершаемая системой в обратимом изобарно-изотермическом процессе. Из уравнения (4.18) получаем для обратимого процесса:
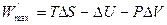. (4.20)
Для необратимого процесса
= 
. (4.21)
Учитывая, что
,
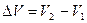получим
. (4.22)
Группируя величины с одинаковыми индексами, находим:
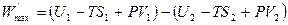. (4.23)
Величину (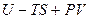 
), которая является функцией состояния, так как 
и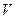 
есть функции состояния, называют энергией Гиббса и обозначают G.
Раньше эту функцию состояния называли изобарно-изотермическим потенциалом.
Таким образом,
G = 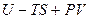. (4.24)
Имея в виду последнее уравнение, можно записать:
,
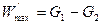или, так как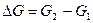 
;
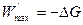. (4.25)
Из уравнения (4.25) следует, что максимальная полезная работа, совершаемая системой в обратимом изобарно-изотермическом процессе, равна уменьшению энергии Гиббса.
Для необратимого процесса путем аналогичного преобразования справедливо
< 
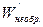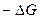, (4.26)
т.е. уменьшение энергии Гиббса в необратимом процессе больше производимой системой работы (полезной).
Зная, что
,
уравнение (4.24) запишем следующим образом:
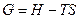(4.27)
или
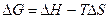. (4.28)
Последнее уравнение может быть представлено следующим образом:
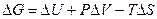(4.29)
или
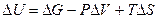. (4.30)
Из этого следует, что изменение внутренней энергии системы можно представить как сумму трех слагаемых:
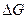–часть внутренней энергии, способная при изобарно-изотермических условиях превращаться в работу;
–часть внутренней энергии, затрачиваемая системой на совершение работы против сил внешнего давления;
–связанная энергия, представляющая собой часть внутренней энергии, которая в указанных условиях не может быть превращена в работу.
«Связанная энергия» тем больше, чем больше энтропия данной системы. Таким образом, энтропию можно рассматривать как меру «связанной энергии».
Определим изменение энергии Гиббса при протекании обратимого и необратимого процессов.
Для этого продифференцируем уравнение (4.27), помня при этом, что дифференциал произведения двух функций равен сумме производных, взятых в предположении, что в данных условиях изменяется только одна из функций, а другая остается постоянной.
В результате дифференцирования получим:
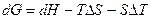. (4.31)
Из соотношений (4.13) и (4.15) следует:
, (4.32)
где знак равенства относится к обратимым, а знак неравенства – к необратимым процессам.
Предполагая, что никакой работы, кроме работы расширения, не производится, получаем:
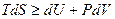. (4.33)
Подставляя найденное значение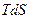 
в уравнение (4.31) и зная, что 
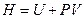, следовательно 
, имеем:
. (4.34)
Из уравнения (4.34) следует, что для обратимых процессов при постоянных Р и T и при условии, что из всех видов работы может производиться только работа расширения,
,
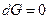так как
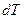и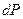 
=0. (4.35)
Поскольку обратимые процессы являются равновесными, т.е. такими, когда система в каждый момент времени находится в состоянии равновесия, то уравнение (4.35) является критерием равновесия.
Протекание необратимых процессов, к которым относятся все самопроизвольные процессы, сопровождается уменьшением энергии Гиббса (Р и Т постоянны), так как при этом
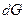< 0. (4.36)
Поэтому неравенство (4.36) является критерием направления самопроизвольных процессов.
Из неравенства (4.36) следует, что при переходе системы из неравновесного состояния в равновесное G уменьшается и в момент равновесия достигает минимального значения:
Gравн. = Gmin. (4.37)
Уравнение (4.37) представляет собой второй критерий достижения равновесия в открытых и закрытых системах.
Дата добавления: 2016-02-09; просмотров: 1320;