Лекция 6. Химическое равновесие в гетерогенных и гомогенных системах
6.1. Взаимосвязь химического потенциала
с другими термодинамическими функциями
С точки зрения термодинамики живые клетки представляют собой открытые системы. Как указывалось ранее, открытой называется система, которая обменивается с внешней средой материей и энергией. Основополагающие термодинамические уравнения, написанные для изолированных и закрытых систем, должны быть в этом случае модифицированы. В них необходимо ввести члены, отражающие изменения массы системы. В этом случае дифференцирование уравнения для термодинамических функций U, Н и G будут иметь следующий вид:
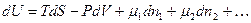 (6.1)
(6.1)
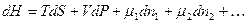 (6.2)
(6.2)
 (6.3)
(6.3)
где m – химический потенциал, n – число молей соответствующего компонента. Каждому компоненту системы в уравнении соответствует свой член mdn. Если в правой части каждого уравнения все переменные, за исключением n1, будут оставаться постоянными, то мы получим следующий ряд равенств:


а также из уравнения (6.1)

Из приведенных выше уравнений видно, что в зависимости от того, какие величины остаются постоянными, химический потенциал представляет собой парциальную молярную внутреннюю энергию, энтальпию или свободную энергию. Поскольку химические процессы в живых клетках и в большинстве экспериментальных систем in vitro протекают при постоянной температуре и при постоянном давлении, наиболее полезным является определение химического потенциала как парциальной молярной свободной энергии. При обсуждении свободной энергии Гиббса мы подчеркиваем значение этой величины как критерия равновесия в системах при постоянных Т и Р: равновесие достигается при DG = 0.
Следовательно, когда свободная энергия перестает в системе меняться, химический потенциал любого компонента системы остается постоянным.
Таким образом, условие равновесия может быть записано как DmI = 0 при Р и Т = const.
Аналогично тому, как мы определяли стандартные изменения для других термодинамических функций и получали стандартные ΔН°,ΔS°и ΔG°, мы можем определить также стандартный химический потенциал μ°как изменение свободной энергии на 1 моль вещества, образующегося, расходующегося или переходящего из одной фазы в другую в своем стандартном состоянии (т.е. при давлении в 1 атм, при определенной температуре и в стандартной эталонной форме).
6.2. летучесть
Стремление к улетучиванию. При описании поведения гетерогенной фазы (например, жидкости, контактирующей с газовой фазой, или твердого вещества в присутствии своих паров) очень часто пользуются понятием летучесть.
Летучесть определяется притяжением между молекулами. Другими факторами, определяющими летучесть, являются кинетическая энергия молекул вещества, его форма, размер и т.д. Наиболее удобным параметром, отражающим летучесть, является давление пара данного вещества. Если в газовой фазе присутствует более чем одно вещество, равновесные давления каждого из них называют парциальными давлениями пара в соответствии с определениями, данными законом парциальных давлений Дальтона.
6.3. Идеальный раствор
Как реальные газы при определенных температурах и давлениях по своим свойствам близки идеальным газам, так и реальные растворы при определенных условиях разбавления приближаются к идеальному раствору.
Идеальным является такой раствор, в котором свойства, присущие растворителю и растворенному веществу, не меняются из-за присутствия новых компонентов, если не считать возможных изменений этих свойств при разбавлении.
Стремление к улетучиванию для молекул растворителя или растворенного вещества уменьшается только в той мере, в которой наличие молекул другого компонента пространственно затрудняет или вообще делает невозможным уход молекул из раствора. В случае идеальных растворов объем является аддитивным, а температура при смешивании не изменяется.
В реальных растворах растворитель и растворенное вещество взаимодействуют друг с другом. Например, если спирт обладает низкой летучестью из-за сильного диполь-дипольного взаимодействия, то при смешивании его с бензолом вследствие разделения диполей полярные молекулы спирта легче переходят в газовую фазу, и парциальное давление его пара будет выше. Возможно и наоборот в случае, например, растворения неполярного вещества в полярном растворителе.
Для того, чтобы применять законы для идеальных растворов в случае реальных, необходимо введение некоторых ограничений. Один из таких принципов носит название предельного закона. Он гласит, что если содержание растворенных молекул в растворе относительно мало, то взаимодействие между ними будет минимальным и, следовательно, они будут слабо влиять на поведение растворителя.
Таким образом, законы идеальных растворов можно применять к реальным растворам, если речь идет о разбавленных. Для рассмотрения свойств реальных растворов при относительно высоких концентрациях растворенного вещества имеются также уравнения, однако они достаточно сложны.
Прежде чем приступить к обсуждению некоторых относительно простых уравнений, тем не менее, позволяющих рассчитывать давление пара, точку замерзания, точку кипения, а также осмотическое давление растворов, познакомимся с двумя фундаментальными соотношениями, лежащими в основе предельных уравнений, – с правилом фаз и уравнением Клаузиуса-Клапейрона.
Правило фаз. На рис. 6.1 показана фазовая диаграмма, количественно описывающая поведение гетерогенной системы, содержащей гомогенные области-фазы. Фазы отделены друг от друга заметными границами, которые называют поверхностями раздела. Каждая фаза гомогенна, однако она не непрерывна. Число фаз равно числу отделенных друг от друга структур, существующих в различных физических состояниях в системе. В одной системе могут существовать несколько жидких или твердых фаз, например: вода – масло, лед – твердая соль. Различают как число фаз, так и число компонентов, образующих фазу.Под числом компонентов понимают число независимых химических индивидуальностей. На рис. 6.1 показана хорошо известная фазовая диаграмма воды. Она является однокомпонентной. Если в воде растворить соль, то получим двухкомпонентную систему. Если растворить два белка в буфере, получим пятикомпонентную систему – два белка, вода, соль и кислота.
Изучение гетерогенных систем сильно упростилось после предложенного в 1874 году Гиббсом обобщения, которое получило название «правило фаз». Оно состоит из очень простого соотношения: а = с – р + 2, где с – число компонентов системы, р – число фаз и f – число степеней свободы системы, т.е. число независимых переменных – таких, как температура, давление и концентрация, которые необходимы для полного описания системы.
Согласно альтернативной формулировке правила фаз, число степеней свободы – это число независимых переменных, которые могут быть изменены без изменения числа фаз. Правило фаз применимо только для систем, находящихся в равновесии.
Посмотрим на фазовую диаграмму воды. Поскольку вода является единственным компонентом, значит с = 1. Вода существует в трех фазах – твердой, жидкой и газообразной. При этом число фаз, которые существуют в равновесии, зависит от температуры и давления.
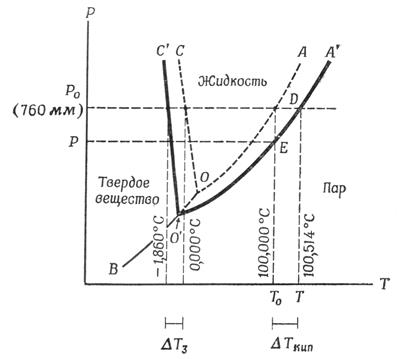
Рис. 6.1. Фазовая диаграмма воды и гипотетического 1 т идеального раствора (масштаб не соблюдается)
Линия ОА представляет собой кривую давления паров воды. Вдоль этой линии вода и пар находятся в равновесии друг с другом. Экспериментально такую линию получают путем измерения давления пара чистой воды при разных температурах.
Линия ОВ является кривой сублимации льда. Выше этой кривой вода существует в виде льда, ниже – в виде пара. В равновесии лед и пар находятся только вдоль линии ОВ, которая и является границей этих двух фаз.
Линия ОС описывает зависимость точки плавления льда от давления; лед и жидкая вода этой линии находятся в равновесии. Наклон линии ОС относительно оси ординат указывает на то, что при увеличении давления точка плавления льда понижается. Три кривые имеют общую точку пересечения 0, известную под названием «тройной точки».
6.4. Фазовая диаграмма содержит зоны,
линии и тройную точку
Для зоны с = 1, р = 1 и f = 2. Для линий с = 1, р = 2 и f = 1. Для тройной точки с = 1, р = 3 и f = 0. Что означают различные степени свободы? То, что внутри зон f = 2, означает следующее: для описания поведения системы мы должны использовать и температуру и давление, т.е. обе величины могут меняться без изменения числа фаз, значит вода существует в жидком состоянии при различных температурах и давлениях. f = 1 означает, что мы можем установить точку на линии, т.е. описать систему только температурой или давлением. Т.е. вдоль линии каждой температуре соответствует строго определенное давление пара. При любом давлении пара для льда существует только одна точка для температуры плавления. В тройной точке система инвариантна, т.е. f = 0, т.е. система может находиться в равновесии только при одном значении температуры и давления.
6.5. Уравнение Клаузиуса-Клапейрона
Из рис. 6.1 видно, что наклон ВО и ОА на графике задается производной dp/dT, которая представляет собой скорость изменения давления пара от Т. Наклон ОС численно равен dp/dT – величина, обратная скорости, с которой точка плавления изменяется при изменении давления. Уравнение, которое связывает эти изменения с другими измеряемыми свойствами системы, было предложено в 1834 году Б. Клапейроном и позже модифицировано Р. Клаузиусом.
Это уравнение можно вывести, используя термодинамические соотношения для химического потенциала. В принципе любые свойства (такие, как объем, энтальпия, свободная энергия) зависят от количества вещества и являются экстенсивными. Однако если они относятся к одному молю вещества в строго определенных условиях, они становятся характеристичными свойствами вещества при данных условиях.
Объем, реально занимаемый одним молем растворенного вещества, называется парциальным молярным объемом растворенного вещества. Он соответствует изменению общего объема очень большого количества раствора при добавлении одного моля растворенного вещества. Очевидно, что при добавлении одного моля растворенного вещества концентрация не будет меняться только при условии бесконечно большого объема исходного раствора.
В этом случае для парциального объема можно записать:
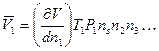 ,
,
где V – общий объем раствора, Т – температура, Р –давление, n – число молей других веществ. Величина V является функцией Т и Р, а также состава раствора.
Если компонент распределен между двумя фазами a и b, то при равновесии ma=mb. В случае однокомпонентной системы химический потенциал равен величине свободной энергии, приходящейся на 1 моль: ma= `G aи mb= `Gb.
Если maбудет слегка меняться при небольших изменениях Т и Р, то аналогичное изменение будет наблюдаться и для mb(при сохранении равновесия). Поэтому можно записать  .
.
Далее мы знаем, что
dG = Vdp-SdT. (6.4.)
Подставим в это уравнение выражение для парциальных молярных величин
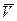 adp - `S adT = `Vbdp - `S bdT. (6.5)
adp - `S adT = `Vbdp - `S bdT. (6.5)
Преобразуем выражение (6.5) в виде члена dp/dT
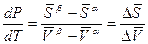 . (6.6)
. (6.6)
Выражение DS по второму началу термодинамики 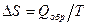 , где Qобр представляет собой молярную теплоту испарения или молярную теплоту плавления.
, где Qобр представляет собой молярную теплоту испарения или молярную теплоту плавления.
Подставим DS в уравнение (6.6) и получим уравнение Клапейрона:
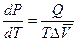 . (6.7)
. (6.7)
В таком виде это уравнение нельзя проинтегрировать. Р. Клаузиус предложил несколько допущений, что позволяет преобразовывать уравнение в более удобную форму – например, в случае равновесия пар – вода 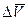 равно (
равно ( 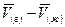 ). Величина `Vждля воды составляет приблизительно 0,1% от `Vги поэтому `Vжможно не учитывать в члене `V(г)– `V(ж). Тогда придем к уравнению
). Величина `Vждля воды составляет приблизительно 0,1% от `Vги поэтому `Vжможно не учитывать в члене `V(г)– `V(ж). Тогда придем к уравнению
 . (6.8)
. (6.8)
Если принять, что пар подчиняется законам идеального газа, то вместо  запишем RT / P:
запишем RT / P:
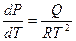 .
.
Заменим выражение для Q более традиционным DНV, получим уравнение Клаузиуса-Клапейрона в обычной форме:
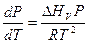 . (6.9)
. (6.9)
Это уравнение можно проинтегрировать, если предположить, что молярная теплота испарения DНVявляется постоянной, т.е. не зависит от температуры. После интегрирования в пределах между Р1, Т1и Р2, Т2получаем:

или в форме
 . (6.10)
. (6.10)
6.6. Коллигативные свойства растворов
Рассмотрим, что происходит с растворителем, если в нем растворяют твердое вещество с исчезающе малым давлением пара. Некоторые свойства растворителя могут зависеть лишь от числа добавленных новых частиц. Интересно, что некоторые эти свойства мало зависят от природы растворенного вещества. Это происходит в том случае, если растворенное вещество не взаимодействует с растворителем и не подвергается ассоциации и диссоциации, т.е. число молекул сохраняется постоянным. В таком случае говорят о коллигативных растворах или о коллигативных свойствах растворов.
Четыре свойства из группы коллигативных свойств обычно рассматриваются вместе: понижение давления пара, повышение точки кипения, понижение точки замерзания и осмотическое давление.
Закон Рауля. Точные измерения, которые позволили математически описать влияние растворенного вещества на физические свойства растворителя, были сделаны впервые Ф.-М. Раулем, работавшим в университете Гренобля в середине и конце XIX века (1830-1901 гг.).
Ф.-М. Рауль обнаружил, что давление пара раствора, содержащего нелетучее растворенное вещество, прямо пропорционально концентрации растворителя. Математически это можно записать так:
Р = kx1,
где Р – давление пара раствора, k – константа пропорциональности, х1 – молярная доля растворителя. Когда растворенное вещество отсутствует х1= 1, то коэффициент k численно равен давлению пара чистого растворителя – Р0. Значит
Р = Р0х1. (6.11)
Поскольку х1+ х2= 1,0, где х2– молярная доля растворенного вещества, то мы можем преобразовать уравнение (6.11) в (6.12), подставив вместо х1 = 1 ‑ х2:
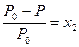 . (6.12)
. (6.12)
Это уравнение показывает, что относительное понижение пара растворителя равно мольной доле растворенного вещества и что давление пара раствора пропорционально молярной доле растворителя. Уравнения (6.11) и (6.12) отражают закон Рауля в преобразованной форме. Закон Рауля и уравнения (6.11) и (6.12) позволяют определить чистоту растворителя и наличие в нем нелетучих веществ.
6.7. Понижение точки замерзания и повышение точки
кипения растворов
Понижение точки замерзания и повышение точки кипения растворов являются прямыми следствиями понижения давления пара.
Рассмотрим двухкомпонентную систему. При растворении одного вещества число химических индивидуальностей возрастает до 2. По правилу фаз
f = c – p + 2 = 2 – p + 2 = 4 – p.
Если существует лишь одна фаза, то у системы должно быть три степени свободы: температура, давление и концентрация.
Рассмотрим вывод формулы для определения повышения точки кипения.
Для этого возьмем уравнение Клаузиуса-Клапейрона поскольку оно является основополагающим соотношением, связывающим давление пара и температуру:
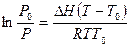 ,
,
где P0и Т0– давление пара и температура кипения чистого растворителя.
Сделаем некоторые упрощения.
а) В соответствии с законом Рауля для идеальных растворов нелетучих веществ P = P0x1.
логарифмирование обеих частей уравнения дает:
lnP = lnP0+ ln x1
или
ln (P0/P) = –ln x1 = –ln (1-x2).
В соответствии с теоремой Маклорена имеем:
–ln(1-x2) = x2+ 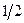 x22+ 1/3 x23+ …
x22+ 1/3 x23+ …
Поскольку величина х2для разбавленных растворов значительно меньше 1, то можно считать, что –ln(1 – х2) » х2.
б) Молярная доля растворенного вещества х2равна n2/(n1+ n2); для разбавленных растворов можно записать, что х2» n2/n1.
в) Поскольку изменение Т происходит в очень узком интервале температур, то Т практически равно Т0. Поэтому вместо Т0Т подставим Т02. Величину Т – Т0в числителе обозначим DТкип.
Сделав эти упрощения и подставив в уравнение Клаузиуса-Клапейрона, получим:
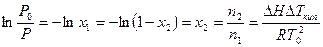 . (6.13)
. (6.13)
Для 1000 г воды в качестве растворителя n1= 1000/18 = 55,6, а n2– это моляльность раствора. Подставим в это уравнение вместо n2/n1значение 0,018m. Решая уравнение относительно величины DТкип,т.е. повышения температуры кипения, получаем:
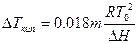 . (6.14)
. (6.14)
Т кипения воды при давлении 1 атм равна 373,15°. При этой температуре и давлении 1 атм молярная теплота ее испарения равна 18 ´ 539 кал, R = 1,987 кал/моль×град. Тогда
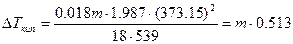 .(6.15)
.(6.15)
Таким образом, мы получили значение эбулиоскопической константы для водных растворов. Аналогично можно получить и соответствующее выражение для криоскопической константы. Размерность этих констант град/моль.
В общем виде уравнение, связывающее изменение температуры кипения или замерзания растворов в сравнении с чистым растворителем, выглядит так:
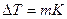 , (6.16)
, (6.16)
где К – эбулиоскопическая или криоскопическая константа, m – моляльная концентрация раствора.
6.8. Осмотическое давление
Живым системам присущи различные физико-химические механизмы транспорта растворителя и растворенных веществ. Различают активный и пассивный транспорт. Активный транспорт характерен для живых мембран. Мы пока остановимся на пассивном транспорте, который более изучен и лучше может быть описан математически. Так, в 1748 году А. Ноллет впервые наблюдал, как растворитель проходит через мембрану из разбавленного раствора в более концентрированный. Если к более концентрированному раствору приложить давление, то в зависимости от его величины течение растворителя может быть замедлено, остановлено или обращено.
Осмотическим давлением раствора называется то наименьшее давление, которое, помимо давления самого растворителя, необходимо приложить к раствору, чтобы предотвратить перетекание растворителя к раствору через мембрану, разделяющую раствор и растворитель, причем мембрана непроницаема для молекул растворенного вещества (полупроницаема) в направлении от чистого растворителя к раствору. Растворитель может перетекать из более разбавленного раствора в более концентрированный даже в том случае, если единственной разделяющей поверхностью между двумя растворами будет слой пара.
По-видимому, осмотические эффекты не должны зависеть от природы мембран, используемых для их измерения. В противном случае можно бы было построить вечный двигатель, используя этот эффект.
В 1877 году В. Пфеффер измерил осмотическое давление П нескольких растворов, приготовленных из одного и того же количества вещества в разных объемах растворителя. При этом он показал, что при постоянной температуре произведение П V всегда одно и то же. Он обнаружил также, что для данного раствора с повышением температуры осмотическое давление растет, однако отношение П/Т сохраняется постоянным. Датский химик Я.Вант-Гофф обобщил результаты и предложил эмпирическое уравнение для описания осмотического давления растворов. Это уравнение имеет вид:
П = CRT, (6.17)
где П – осмотическое давление, С – молярная или моляльная концентрация раствора, а Т – температура. Линейная зависимость П от С и Т соблюдается только для идеальных растворов. Таким образом, уравнение Вант-Гоффа служит еще одним примером предельного закона.
Однако уравнение осмотического давления можно однозначно вывести, исходя из теоретических соображений. Осмотическое давление раствора можно интерпретировать как следствие того факта, что давление пара раствора нелетучего вещества ниже, чем давление пара чистого растворителя.
Уравнение осмотического давления легко получить, если предположить, что пар растворителя ведет себя как идеальный газ. Когда раствор отделен от чистого растворителя полупроницаемой мембраной и система путем увеличения общего давления на раствор приведена к равновесию, свободная энергия на моль растворителя должна быть одинакова по обе стороны от мембраны. Уменьшение свободной энергии на моль растворителя в растворе (по сравнению с его свободной энергией в стандартном состоянии) выражается уравнением (6.14):
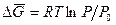 . (6.18)
. (6.18)
Увеличение давления, которое приложено к раствору, должно быть достаточным для того, чтобы восстановить свободную энергию растворителя в растворе до свободной энергии чистого растворителя. Это увеличение свободной энергии зададим уравнением
dG = VdP при Т = const, (6.19)
так как жидкость несжимаема:
DG = VDР . (6.20)
Увеличение давления и есть по существу осмотическое давление, т.е. DР = П.
Молярный объем растворителя обозначается символом V. Следовательно, для жидкости 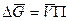 .
.
При равновесии П
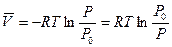 , (6.21)
, (6.21)
откуда
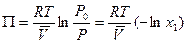 . (6.22)
. (6.22)
Для разбавленных растворов 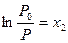 .
.
Подставим в уравнение (6.22) и получим:
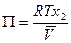 . (6.23)
. (6.23)
Поскольку для разбавленных растворов х2» n2/n1, то  ;
;
 – равен объему растворителя и приблизительно объему раствора (для разбавленных растворов). В результате получим:
– равен объему растворителя и приблизительно объему раствора (для разбавленных растворов). В результате получим:
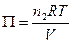 . (6.24)
. (6.24)
Уравнение (6.24) является специальным случаем уравнения идеального газа применительно к осмотическому давлению. Его можно использовать не только для разбавленных растворов, однако требуется, чтобы пар растворителя вел себя как идеальный газ.
Однако нельзя дать ввести себя в заблуждение видом уравнения и его сходством с уравнением идеального газа, поскольку нет оснований полагать, что осмотическое давление возникает за счет бомбардировки стенок сосуда молекулами растворенного вещества. Из уравнения лишь следует, что растворение одного моля вещества в одном литре растворителя при 0 ºС в идеальном случае будет вызывать повышение осмотического давления на 22,41 атм. Реальные растворы в таких концентрациях дают заметные отклонения от предсказанных осмотических давлений, подобно тому как это имеет место при вычислении точек замерзания и точек кипения.
Уравнение (6.24) можно преобразовать в форму, содержащую молекулярную массу растворенного вещества М. Подставим вместо числа молей растворенного вещества n2величину g/M, получим:
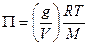 или
или  , (6.25)
, (6.25)
где С – концентрация в граммах на л. При делении обеих частей на С слева появляется член П/С, который называется приведенным осмотическим давлением. В идеальных растворах П/С должна оставаться постоянной, т.е. не зависеть от концентрации. Однако это не всегда соблюдается. Общее уравнение для таких случаев имеет вид:
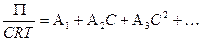 , (6.26)
, (6.26)
где А1 = 1/МN, а МN– среднестатистический молекулярный вес. Для сильно разбавленных растворов при экспериментально измеряемых концентрациях малыми членами можно пренебречь, и уравнение будет иметь вид:
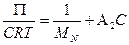 . (6.27)
. (6.27)
Такое уравнение правомерно при следующих условиях:
1) величина А2не очень велика;
2) величина МNне очень велика.
Уравнение (6.27) является уравнением прямой линии с наклоном, численно равным величине А2, называемой «вторым вириальным коэффициентом». Прямая пересекает ось П/CRT в точке, соответствующей величине, обратной MN. Поэтому метод осмотического давления используется для определения молекулярных весов полимеров. Наиболее точные результаты получаются для полимеров с молекулярными весами, лежащими между 10 000 и 20 0000.
6.9. Растворы электролитов
П = iCRT, где i – изотонический коэффициент:
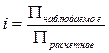 .
.
Для слабых электролитов i равно отношению фактического числа частиц растворенного вещества к тому числу, которое было бы в отсутствие диссоциации.
Расчет изотонического коэффициента: до диссоциации N частиц, a – степень диссоциации, тогда число диссоциированных частиц – aN, а недиссоциированных – (1–a)N, k – количество образующихся ионов. Тогда при диссоциации образуется aN частиц aNk – ионов. Общее число частиц равно:
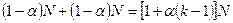 .
.
Отсюда изотонический коэффициент:
 или i = 1+a(k-1).
или i = 1+a(k-1).
Для NaCl « Na++ Cl- k = 2 i = 1 + a;
Для Na2SO4« 2 Na++ SO4- k = 3 i = 1 + 2a;
Для Na3PO4« 3Na++ PO43- k = 4 i = 1 + 3a и т.д.
Для сильных электролитов a = 1.
Дата добавления: 2016-02-09; просмотров: 1302;
