Активные центрыгетерогенных катализаторов
Многочисленные экспериментальные данные о гетерогенных каталитических реакциях привели к заключению о том, что каталитически активной является не вся поверхность катализатора, а только небольшая ее часть. Об этом свидетельствуют факты, полученные при изучении адсорбции, отравления катализаторов, влияния характера поверхности на каталитическую активность и др.
Если следовать теории адсорбции Лэнгмюра, согласно которой поверхность является однородной, то изотерму адсорбции можно представить в виде линейного уравнения
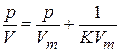 . (25.1)
. (25.1)

|
Рис. 25.1. Изотермы адсорбции газа Рис. 25.2. Теплота адсорбции газа
на твердом адсорбенте при разных на поверхности катализатора
температурах: (Т1 > Т2 > Т3 > Т4)
Если это уравнение справедливо, то должна существовать линейная зависимость в координатах р/V – р, по которой можно определить параметры Vm и K. Однако во многих случаях такая линейная зависимость отсутствует, но в небольших интервалах давлений можно выделить отдельные линейные участки (рис. 25.1). Такую зависимость можно объяснить, если предположить, что разные участки поверхности имеют разные адсорбционные потенциалы.
Адсорбционная неоднородность поверхности подтверждается также данными о теплотах адсорбции. При последовательной адсорбции одинаковых порций какого-либо газа на поверхности катализатора теплота адсорбции закономерно убывает, т.е. все менее и менее активные участки поверхности заполняются адсорбатом (рис. 25.2).
Данные о действии ядов также показывают, что активность различных участков поверхности катализаторов не одинакова. Каталитическая активность многих катализаторов практически полностью теряется, когда доля адсорбированного яда составляет всего лишь 0,5 – 1% от предельной адсорбции. Отсюда следует, что поверхность состоит из совокупности адсорбционных центров, но лишь небольшая их часть является каталитически активными, т.е. нельзя отождествлять понятия адсорбционного и каталитически активного центров.
Еще в 20-х годах ХХ века Тейлор предложил теорию, согласно которой активными центрами катализатора являются поверхностные атомы кристаллической решетки, находящиеся выше среднего уровня поверхности. Такие “пики” обладают свободными валентностями и способны к образованию реакционно-способных промежуточных соединений.
Так как адсорбция реагирующих молекул является обычно активированной, то следует полагать, что при взаимодействии адсорбционного центра с молекулой субстрата образуется поверхностное соединение хемосорбционного типа. Отсюда следует вывод о том, что каталитически активными будут только те адсорбционные центры или их совокупность, которые способны образовывать с адсорбирующимся веществом активное промежуточное поверхностное соединение. Существенным фактором, определяющим возможность образования такого соединения, является характер поверхности.
Если рассматривать идеальный кристалл при температуре абсолютного нуля, то все его частицы занимают строго определенные положения, образуя правильную кристаллическую решетку. При повышении температуры этот порядок нарушается. Некоторые частицы покидают свои места в узлах решетки и занимают положения в междоузлиях (“дефекты по Френелю”) или выходят из них на поверхность (“дефекты по Шоттки”). Образование дефектов в объеме приводит и к образованию дефектов на поверхности, появлению на ней вакантных мест и частиц на гранях в местах, не соответствующих правильному кристаллическому порядку.
В реальных кристаллах всегда имеются различные нарушения кристаллической решетки. К таким нарушениям относятся дислокации – различные искажения плоскостей решетки по сравнению с геометрически правильным их расположением в идеальном кристалле. Стехиометрические нарушения, а также инородные примеси также вызывают местные искажения геометрического порядка в кристалле. Эти искажения могут привести к тому, что кристалл окажется разделенным “трещинами” на отдельные микроскопические блоки, скрепленные между собой. Такое блочное строение характерно для многих кристаллических тел (силикагели, алюмогели, активированный уголь и др.), широко используемых в гетерогенном катализе. В реальном кристалле число дефектов значительно больше, чем в гипотетическом идеальном кристалле. Разнообразные нарушения поверхности резко увеличивают адсорбционную поверхность и число адсорбционных и каталитически активных центров, а поверхность может стать энергетически неоднородной.
В теориях гетерогенного катализа рассматриваются различные модели строения поверхности.
Однородная поверхность представляется как поверхность, на всех адсорбционных центрах которой теплота адсорбции одинакова, а каталитическое превращение идет с одной и той же энергией активации. Реально такие поверхности встречаются редко и наиболее вероятны для чисто металлических катализаторов.
Неоднородность поверхности может быть выражена в энергетической неравноценности активных центров. Тогда реагирующее вещество, попадающее на поверхность, будет распределяться по центрам адсорбции в соответствии с энергией этих центров и реагировать с соответствующей энергией активации.
Неоднородностьповерхности может быть также геометрической, она определяется блочной разобщенностью поверхности катализатора. Реагирующее вещество, попадая на тот или иной блок, будет адсорбироваться, а если данный центр является и каталитически активным, реагировать на центрах внутри блока, независимо от наличия более энергетически активных центров на других блоках. При этом решающим является не энергетическое распределение, а распределение центров по геометрическим блокам.
Все современные теории гетерогенного катализа основываются на представлениях о существовании каталитически активных центров, но конкретное строение таких центров в различных теориях предполагается разным.
25.2. Мультиплетная теория катализа
Накопившийся опытный материал дал возможность конкретизировать понятие активный центр и сопоставить его строение и состав со строением молекул, которые подвергаются превращению. Впервые это сделано в мультиплетной теории А. А. Баландина(1929г.), в которой рассматривается активный центр гетерогенного катализатора.
Основные положения этой теории следующие:
1. Каталитически активный центр представляет собой совокупность определенного числа адсорбционных центров, расположенных на поверхности в геометрическом соответствии со строением молекулы, которая подвергается превращению. Это положение получило название принципа геометрического (структурного) соответствия.
2. При адсорбции молекул на активном центре образуется мультиплетный комплекс, в результате чего происходит перераспределение связей, которое в результате и приводит к образованию продуктов реакции.
Таким образом, в теории каталитическое действие связывается с зависимостью между геометрическим расположением адсорбционных центров и геометрией реагирующей молекулы. Для различных реакций число адсорбционных центров (каждый из которых отождествляется с одним атомом металла) в активном центре может быть равным 2, 3, 4, 6 и т.д. Эти активные центры называются дублетами, триплетами, квадруплетами, секстетами, а в общем случае – мультиплетами.
Например, дегидрирование этилового спирта, согласно теории мультиплетов, происходит на дублете, при этом к одному атому дублета притягиваются водородные атомы групп СН2 и ОН, а к другому – атом кислорода и углеродный атом группы СН2. В результате происходит разрыв связей С–Н и О–Н и образование связей Н–Н и С=О с образованием молекул уксусного альдегида и водорода:
|


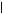
 Н Н Н Н
Н Н Н Н
|
|
|



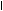
 Н– С – С – О
Н– С – С – О  Н – С – С О
Н – С – С О
Н Н Н Н Н – Н
При других расстояниях между атомами катализатора в дублете возможен другой процесс: водородный атом группы СН3 и кислородный атом притягиваются к одному атому катализатора, а оба углеродных атома – к другому:
|



 Н Н Н Н
Н Н Н Н
|

|
|
 Н– С – С – Н
Н– С – С – Н  Н– С С – Н
Н– С С – Н
Н О – Н Н – О – Н
В результате реакции образуются этилен и вода.
В реакциях дегидрирования циклопарафинов катализаторами являются металлы с гранецентрированными или гексагональными кристаллическими решетками, но только те, у которых расстояния между центрами атомов в решетке лежит в пределах от 24,8 до 27,7 нм (Ni, Cu, Rh, Ir, Pd, Pt). Металлы с аналогичными кристаллическими решетками, но с другими межатомными расстояниями (Th, Pb, Au, Ag) каталитической активности при дегидрировании шестичленных колец не проявляют.
Это объясняется тем, что должно соблюдаться геометрическое соответствие между активным центром и молекулой. Тот факт, что каталитически активными являются металлы с несколько отличающимися межатомными расстояния, свидетельствует о том, что при образовании мультиплетного комплекса возможна некоторая деформация валентных углов.
Схематически расположение частиц в мультиплетном комплексе при дегидрировании циклогексана на секстете представлено на рис. 25.3.
При перераспределении связей на активном центре углеродные атомы 1 и 6 притягиваются к атому катализатора б, 5 и 4 – к атому г, а 3 и 2 – к атому е, а атомы водорода СН2 групп притягиваются к атомам катализатора а, в и д. В результате разрываются шесть связей С–Н, образуется три связи С=С и три связи Н–Н, т.е. продуктами являются молекула бензола и три молекулы водорода.
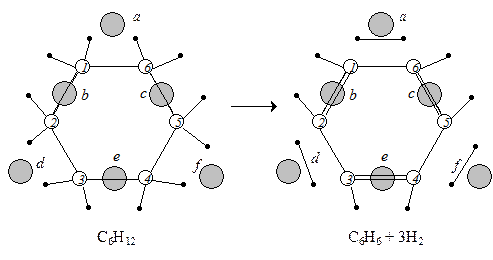 Рис.25.3. Схема дегидрирования циклогексана
Рис.25.3. Схема дегидрирования циклогексана
|
Таким образом, мультиплетная теория дает возможность качественно объяснить эмпирические закономерности, установленные при изучении каталитических превращений многих органических веществ. Однако в последующих работах были обнаружены и отступления от простой схемы геометрического соответствия. Например, оказалось, что активный центр дегидрирования циклогексана на Cr2O3 состоит не из шести, а из двух атомов, а на том же катализаторе при определенных условиях могут быть дегидрированы и пятичленные циклы. Все это показывает, что истинный механизм каталитического действия сложнее простой схемы мультиплетной теории.
Кроме принципа геометрического соответствия в теорию позже было внесено еще одно положение – принцип энергетического соответствия. В соответствии с этим принципом энергия активации гетерогенной каталитической реакции является сложной величиной, которую можно в первом приближении представить зависящей от двух составляющих. Первая из них определяется энергией связи между атомами в реагирующей молекуле, а другая – энергией взаимодействия реагирующей молекулы с атомами катализатора при образовании мультиплетного комплекса. Отсюда вытекает положение о зависимости каталитической активности катализатора от его сродства к реагирующим частям молекулы. Представим гетерогенную каталитическую реакцию следующей схемой:
Исходные вещества + Катализатор ® Мультиплетный комплекс ®
Катализатор + Продукты реакции
Для протекания первой стадии (образования мультиплетного комплекса) реагирующая молекула должна получить энергию, необходимую для разрыва связей. С другой стороны, при этом выделяется энергия образования мультиплетного комплекса. В первом приближении разность этих энергий и есть энергия активации. При очень малом сродстве катализатора к субстрату снижение энергии активации будет незначительным, а каталитическая активность – низкой. По мере увеличения сродства катализатора к субстрату энергия активации все больше понижается и каталитическая активность возрастает. Но продукты реакции образуются на второй стадии – распада мультиплетного комплекса. Для осуществления этой стадии мультиплетный комплекс должен получить энергию, необходимую для разрыва связей в нем, при этом же выделяется энергия образования конечных продуктов. Скорость второй стадии и определяется разностью этих энергий. Поэтому увеличение сродства катализатора к субстрату приводит к ускорению каталитического процесса только до определенного предела, пока скорость реакции определяется первой стадией. При значительном увеличении прочности связи в мультиплетном комплексе общая скорость реакции будет определяться второй стадией, энергия активации которой будет возрастать, что приведет к торможению процесса.
25.3. Теория активных ансамблей
 Рис.25.4. Распределение атомов катализатора по областям свободной миграции катализатора: геометрические барьеры на поверхности носителя (а,б); энергетические барьеры на поверхности носителя (с)
Рис.25.4. Распределение атомов катализатора по областям свободной миграции катализатора: геометрические барьеры на поверхности носителя (а,б); энергетические барьеры на поверхности носителя (с)
|
Как уже отмечалось, теория мультиплетов в первую очередь применима для объяснения каталитического действия металлических катализаторов со сравнительно однородной поверхностью. В промышленном производстве очень часто применяются катализаторы на носителях, т.е. такие, у которых каталитически активное вещество наносится на поверхность какого–либо твердого тела с хорошо развитой поверхностью (силикагель, алюмогель, асбест, активированный уголь и т.п.). Носитель сам по себе не проявляет каталитического действия, но он увеличивает удельную активность катализатора, в небольших пределах может изменять каталитическую активность, а иногда и избирательность, повышает термическую устойчивость и устойчивость к ядам.
Эти эффекты можно связать с блочным строением поверхности носителя. Наличие различных микротрещин и других дефектов приводит к тому, что поверхность носителя состоит из большого числа отдельных микроучастков (блоков), разделенных геометрическими и энергетическими барьерами. Атомы катализатора, попадая на отдельные блоки, могут перемещаться по поверхности лишь в пределах блока, так как для перехода на соседний блок требуется избыточная энергия для преодоления барьера (рис. 25.4).Эти блоки Н.И.Кобозев назвал “областями свободной миграции”, или просто “областями миграции”.
Таким образом, нанесенные атомы катализатора располагаются на поверхности в виде отдельных агрегатов, “ансамблей”, состоящих из некоторого числа атомов, локализованных в областях миграции.
Определим общую каталитическую активностьА катализатора как число молекул субстрата, реагирующих в 1 с на всех атомах катализатора, находящихся на поверхности 1 г образца. Если каталитически активными будут любые комбинации атомов катализатора, находящихся на поверхности носителя в областях миграции, то общая каталитическая активность должна быть прямо пропорциональна числу нанесенных атомов катализатора N, а удельная активность (активность на один атом катализатора) а = А/N должна быть постоянной. Если же каталитически активными будут лишь определенные сочетания атомов (п-атомные ансамбли), каталитическая активность будет пропорциональна вероятности образования п–атомного ансамбля.
Многочисленные исследования показали, что в большинстве случаев кривые зависимости общей активности от числа нанесенных атомов катализатора имеют максимум, а удельной активности – также имеют максимум или уменьшаются по экспоненте при увеличении N. Таким образом, опыт подтвердил избирательность каталитического действия различных ансамблей. Исходя из этих данных, Н.И.Кобозев в 1939 г. разработал теорию, которая получила название теории активных ансамблей.
Основное положение теории можно сформулировать следующим образом: носителем каталитической активности является находящаяся на поверхности атомная (докристаллическая) фаза катализатора, относительно которой поверхность носителя (или кристаллическая фаза самого катализатора) является инертной подкладкой. Для каждого процесса каталитически активным центром является ансамбль из определенного числа п атомов катализатора.
Рассмотрим распределение атомов на поверхности катализатора, состоящего из отдельных областей миграции. Если удельная поверхность носителя S, а средняя величина площади одной области D, то число областей миграции на поверхности 1 г носителя равно
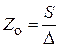 . (25.2)
. (25.2)
Если на поверхность 1 г носителя нанесено N атомов катализатора, то в среднем на одну область приходится
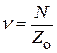 (25.3)
(25.3)
атомов. В действительности же в разные области миграции может попасть разное количество атомов. Вероятность попадания одного атома из их общего числа N в одну из Zoобластей равна 1/Zo , а вероятность попадания n атомов – (1/Zo)n. Остальные (N – n)атомов попадут в любую из оставшихся (Zo – 1) областей. Тогда вероятность Woобразования n-атомного ансамбля атомов катализатора будет
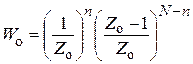 . (25.4)
. (25.4)
Так как все атомы одинаковы и могут быть переставлены местами без изменения распределения, то для получения полной вероятности образования
n-атомного ансамбля вероятность нужно умножить на число сочетаний из N по n:
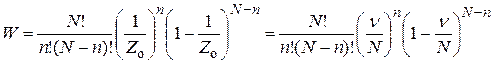 . (25.5)
. (25.5)
Поскольку общее число атомов катализатора N (1020 – 1023) значительно больше числа атомов n в ансамбле (1 – 10), можно использовать предельный переход:
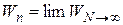 . (25.6)
. (25.6)
Для отдельных сомножителей уравнения (25.5) имеем:
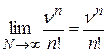 ; (25.7)
; (25.7)
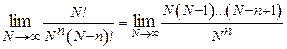
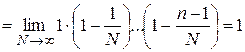 ; (25.8)
; (25.8)
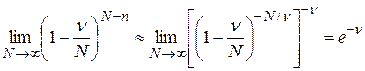 . (25.9)
. (25.9)
Окончательно для вероятности образования получаем
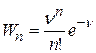 . (25.10)
. (25.10)
Таким образом, видно, что распределение атомов катализатора на блочной поверхности носителя подчиняется закону Пуассона. Как видно из рис. 25.5, все кривые проходят через максимум, т.е. в зависимости от концентрации на поверхности носителя образуются главным образом ансамбли из определенного числа атомов.
Если каталитически активным является лишь определенный n–атомный ансамбль, то число таких ансамблей на поверхности 1 г носителя равно
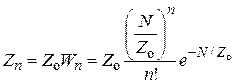 . (25.11)
. (25.11)
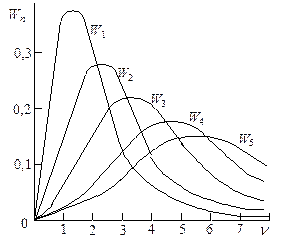 Рис.25.5. Вероятность образования n-атомного ансамбля в зависимости от среднего числа атомов в области свободной миграции
Рис.25.5. Вероятность образования n-атомного ансамбля в зависимости от среднего числа атомов в области свободной миграции
|
Обозначим через rn активность одного n–атомного ансамбля, тогда общая А и удельная а активности катализатора будут равны соответственно:
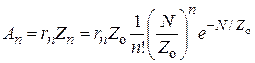 ; (25.12)
; (25.12)
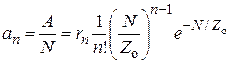 . (25.13)
. (25.13)
Обе эти зависимости дают максимум по N. Продифференцируем их по N:
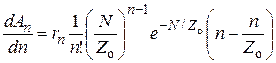 ;(25.14)
;(25.14)
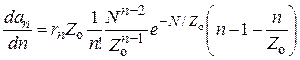 . (25.15)
. (25.15)
Так в точке максимума производные равны нулю, то из уравнений следует:
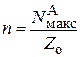 и
и 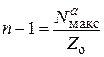 . (25.16)
. (25.16)
Решая эту систему из двух уравнений, получим условия, которые позволяют из экспериментальных данных определять число атомов в активном ансамбле и число областей миграции на поверхности носителя:
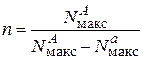 ; (25.17)
; (25.17)
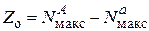 . (25.18)
. (25.18)
Если n = 1, то уравнение (25.9) принимает вид:
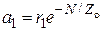 , (25.19)
, (25.19)
т.е. если экспериментальная кривая удельной активности не имеет максимума и экспоненциально спадает с повышением концентрации катализатора, то активным центром является одноатомный ансамбль.
25.4.Электронные представления в гетерогенном катализе
Обязательной стадией гетерогенных каталитических реакций является образование промежуточного соединения адсорбционного типа на поверхности катализатора. Свойства этого соединения определяют направление и, если процесс протекает в кинетической области, его скорость, а также активность катализатора. Свойства самого промежуточного соединения зависят от характера взаимодействия между исходными веществами и активными центрами катализатора на его поверхности, т.е. электронным состоянием поверхности и катализируемых молекул. Изучение состояния хемосорбированных молекул во многих случаях показало, что в хемосорбции на металлах и полупроводниках принимают участие электроны или электронные дырки твердого тела. В связи с этим необходимо исследовать влияние электронных свойств твердых тел на их поведение в процессах адсорбции и катализа. Существование электронного фактора в катализе общепризнанно, однако его трудно описать не только количественно, но даже качественно. Причины этого различны. Прежде всего, вряд ли можно найти реальную систему катализатор – реагент, в которой одновременно с электронными не действовали бы в той или степени другие факторы, например, геометрические. Кроме того, для теоретической интерпретации необходимо точно знать как электронное строение твердого тела, так и характер его взаимодействия с реагентом.
Теоретической основой исследования электронного фактора были в основном теория валентных связей, зонная модель, теория кристаллического поля и теория поля лигандов. Большая часть исследований базировалась на представлении о существовании в твердых телах коллективных электронных состояний (зонная модель), в более новых исследованиях повышено внимание к отдельным ионам на поверхности твердых тел как реакционным центрам, свойства которых описывает теория кристаллического поля и теория поля лигандов.
Полинг предложил разграничить d-орбитали переходных металлов на три типа: связывающие d-орбитали, которые участвуют в ковалентных гибридизациях, металлические d-орбитали и атомные d-орбитали. Он ввел величину d, % d-характера ковалентной связи:
| d = | Число связывающих d- электронов |
 Связывающие электроны + Металлические орбитали Связывающие электроны + Металлические орбитали
|
Например, в никеле по Полингу имеются оба предельных резонансных состояния А и В:
3d 4s 4p
Ni(A) ¯ · · |·|· · ·|
Ni(B) ¯ ¯· · · |·|· · °|
Здесь · – связывающий электрон, ° – металлическая (свободная) орбиталь, – электрон на несвязывающей атомной орбитали. Неспаренные электроны атомных d-орбиталей обусловливают магнитный момент, который для никеля равен 0,6 магнетона Бора. Соотношение количеств резонансных форм А и В равно 30: 70 и степень d- характера никеля d = 40%.
Для данного металла величина d показывает долю участия d-электронов в spd-гибридах и (при учете общего числа внешних и d- и s- электронов) число незанятых атомных d-орбиталей. В зонной модели незанятые атомные
d-орбитали соответствуют электронным дыркам d-зоны. Если при реакции происходит взаимодействие электронов реагента и атомных d-орбиталей катализатора, то можно ожидать корреляции каталитической активности с величиной d. Для гидрирования этилена на различных металлах (никель, платина, палладий, родий) была найдена такая корреляция. Однако истолкование этой корреляции тесно связано с вопросом о содержании теории валентной связи и полученной на ее основе величины d.
В зонной модели металлического состояния функция распределения электронов проводимости описывается статистикой Ферми – Дирака. Применение статистики Максвелла – Больцмана исключается принципом Паули.
При 0 К N имеющихся электронов находятся на N/2 низших энергетических уровнях до уровня Ферми ЕF с энергией Emax – предельной энергией Ферми.
Вероятность W нахождения электрона на некотором уровне описывается как функция абсолютной температуры Т:
W = {[exp(E–Emax)/kT]+1}–1,
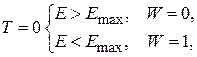
Т =0, Е = Emax, W=1/2 (определение энергии Ферми).
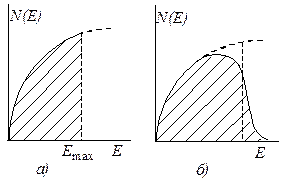 Рис. 25.6. Функции распределения электронной плотности, соответствующие модели свободных электронов при Т = 0 К (а) и Т > 0 К (б). N(E) – плотность состояний, число занятых квантовых состояний.
Рис. 25.6. Функции распределения электронной плотности, соответствующие модели свободных электронов при Т = 0 К (а) и Т > 0 К (б). N(E) – плотность состояний, число занятых квантовых состояний.
|
Из рис. 25.6 следует, что даже при 0 К электроны имеют довольно высокую полную энергию. Например, для меди EF » 7 эВ. В то же время тепловая энергия электронов проводимости при температуре плавления T= 1356 К составляет всего около 0,1 эВ.
Вследствие взаимодействия в кристалле ранее изолированных атомов происходит расщепление уровней энергии внешних электронов и образуются перекрывающиеся (s, p)- и d- зоны, показанные на рис. 25.7. При этом в большинстве случаев заполнение зон в кристалле металла вследствие перекрывания уже не совпадает с последовательностью заполнения электронных уровней изолированных атомов.
Число электронов, которые дополнительно могут разместиться в заданном интервале энергий dE частично заполненной d-зоны переходного металла зависит от вида функции распределения электронной плотности [N(E) = f(E)].
Если при хемосорбции электроны переносятся в d–зону металла, то прочность и число образующихся связей металл – адсорбат зависят не только от наличия дырок в d-зоне, но и от плотности состояний N(E) на поверхности Ферми.
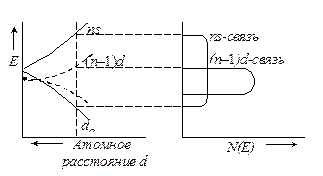 Рис. 25.7. Схема расщепления и перекрывания s- и d-уровней переходного металла
Рис. 25.7. Схема расщепления и перекрывания s- и d-уровней переходного металла
|
Дауденрассмотрел факторы, которые, согласно зонной модели, влияют на образование положительных или отрицательных ионов, а также ковалентных связей на поверхности металла. Он исходил из следующих трех предположений:
1) распределение электронной плотности на поверхности металлического кристалла соответствует распределению электронов в кристалле;
2) лимитирующей стадией катализируемой реакции является образование хемосорбированного комплекса;
3) при адсорбции происходит сдвиг электронного облака адсорбированных частиц или электронов катализатора.
Таблица 25.1
Заполнение зон в некоторых переходных металлах
___________________________________________________________
Металл Электронная конфигурация Заполнение зон
___________________________________________________________
Fe 3d64s2 3d7,054s0,95
Ni 3d84s2 3d9,454s0,55
Pd 4d10 4d9,645s0,36
Pt 5d96s1 5d9,76s0,3
Cu 3d104s1 3d104s1
___________________________________________________________
Сдвиг электронной плотности в направлении металла происходит, например, при адсорбции бензола и олефинов вследствие взаимодействия с p-электронами и при адсорбции водорода вследствие перехода валентных электронов. С металлами VIII группы периодической системы элементов водород связывается в виде протонов, которые размещаются преимущественно в октаэдрических полостях, а электроны водорода переходят в еще целиком не заполненную d-зону (протонная модель растворимости водорода). Согласно Даудену, переносу электронов от адсорбированных частиц к адсорбенту благоприятствуют следующие факторы:
1. Высокое значение работы выхода электрона EeA, при котором поглощению электрона металлом соответствует увеличение общей энергии. Если пренебречь потенциалом поверхности, то = EeA.= EF.
2. Высокая плотность состояний N(EF) электронов на поверхности Ферми. Тогда в примыкающей к уровню Ферми бесконечно малой области энергий dE, где размещаются электроны адсорбированных частиц, имеется большое число незаполненных уровней энергии, которые могут принять значительное число электронов без существенного повышения энергии.
3. Большой положительный градиент плотности состояний на поверхности Ферми ¶N(EF)/¶E, который означает крутой подъем кривой распределения и сильное увеличение числа незаполненных уровней энергии.
Приведенные в таблице 25.2 значения работы выхода электрона указывают на особую роль металлов побочных групп.
Таблица 25.2
Работа выхода электрона различных металлов
____________________________________________________
Металл Е, эВ Металл E, эВ
____________________________________________________
K 2,2 Fe 4,5–4,7
Ca 2,8 Co 5,0
Rb 2,1 Ni 4,4–5,3
Sr 2,4 Pd 5,4
Ti 3,6–4,3 Pt 5,6–5,8
V 3,8 Cu 4,4–5,1
Cr 3,9–4,4 Ag 4,4
Mn 3,8–4,1 Au 4,8–5,5
____________________________________________________
В частности, плотность электронных состояний на поверхности Ферми достигает максимальных значений у Ni, Pd и Pt, которые являются наиболее активными катализаторами реакций активирования водорода.
В зонной модели полупроводников энергетическое состояние, из которого происходит возбуждение электронов, описывается статистикой Ферми – Дирака как уровень Ферми (EF). Уровень Ферми можно рассматривать как электрохимический потенциал электронов в твердом теле. Вероятность того, что уровень Ферми занят электронами, W= 1/2. Поскольку в истинном полупроводнике лишь немногие электроны могут переходить из первоначально целиком заполненной валентной зоны (ВЗ) в зону проводимости (ЗП), для валентной зоны W(E)>1/2, а для зоны проводимости W(E)<1/2. Следовательно, уровень должен лежать между ВЗ и ЗП. У полупроводников n-типа EF лежит между донорным уровнем и уровнем проводимости, а у полупроводников p-типа – между акцепторным уровнем и валентной зоной (рис. 25.8).
Сдвиг уровня Ферми возможен вследствие изменения концентрации донорных или соответственно акцепторных уровней центров, в простейшем случае путем введения ионов противоположного знака. Другие нарушения решетки также могут приводить к появлению уровней энергии внутри запрещенной зоны. К ним принадлежат уровни F-центров. Согласно Тамму, разрыв периодичности идеального кристалла поверхностью также вызывает появление таких уровней энергии (уровней Тамма). В дегидрирующем катализаторе ZnО донорными уровнями являются избыточные (сверхстехиометрические) атомы цинка, находящиеся в междоузлиях решетки. Введение в решетку ZnО однозарядных ионов Li+ уменьшает число донорных центров (рис. 25.9):
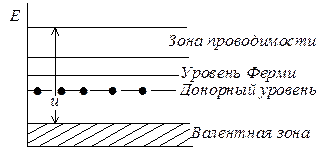 Рис. 25.8. Зонная модель полупроводника n-типа (u – ширина запрещенной зоны; для изолятора u>kT; для полупроводника u<kT)
Рис. 25.8. Зонная модель полупроводника n-типа (u – ширина запрещенной зоны; для изолятора u>kT; для полупроводника u<kT)
|
Zn + Li2O + 1/2O2 ® 2Li+ + Zn2+ + 2O2–
В противоположность введению однозарядных катионов введение ионов с числом зарядов больше 2, например, Аl3+, увеличивает число донорных центров:
ZnO + Al2O3 ® 2Al3+ + 3O2– + 1/2O2 + Zn
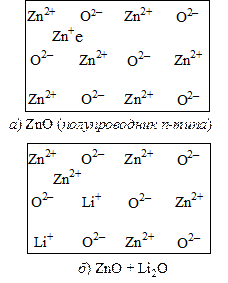 Рис. 25.9. Схема введения оксида лития в оксид цинка
Рис. 25.9. Схема введения оксида лития в оксид цинка
|
Введение посторонних ионов можно экспериментально контролировать, измеряя электронные свойства, которые являются функциями уровня Ферми (электропроводность, работа выхода электрона, термоэлектродвижущая сила). По результатам этих измерений можно судить и о характере взаимодействия адсорбат – адсорбент. Например, в простых случаях хемосорбция кислорода уменьшает электрическую проводимость полупроводника n-типа вследствие притяжения его элементов, но увеличивает электрическую проводимость полупроводника p-типа.
На полупроводниках подробно изучен распад N2O как модельная реакция. Лимитирующей стадией является десорбция кислорода (стадия “в”):
а) N2O + e–кат ® N2O–адс
б) N2O адс ® N2 адс + O–адс
в) O–адс ® 1/2O2газ + e– кат
На лимитирующей стадии происходит присоединение электрона катализатором, чему соответствует общий ряд активности:
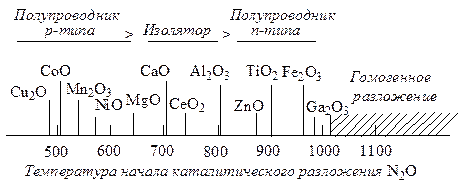
Изменение каталитической активности полупроводникового оксида при введении добавок соответствует указанному механизму разложения N2O: добавление Li2О к ZnO повышает каталитическую активность оксида цинка в отношении этой реакции. Корреляция электронных и каталитических свойств наблюдается и при окислении СО на NiO с добавками.
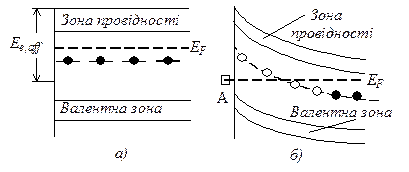 Рис. 25.10. Влияние хемосорбции на энергетическую схему полупроводника n-типа согласно зонной модели: а – вначале хемосорбции вещества А; б – после установления хемосорбционного равновесия Агаз L Аадс; (· – занятый донорный уровень; o – незанятый донорный уровень; Еe,aff – сродство к электрону; А – адсорбируемое вещество)
Рис. 25.10. Влияние хемосорбции на энергетическую схему полупроводника n-типа согласно зонной модели: а – вначале хемосорбции вещества А; б – после установления хемосорбционного равновесия Агаз L Аадс; (· – занятый донорный уровень; o – незанятый донорный уровень; Еe,aff – сродство к электрону; А – адсорбируемое вещество)
|
Примером адсорбции с переносом заряда может служить адсорбция молекул А на полупроводнике n-типа с образованием отрицательно заряженных частиц А–. Относительное положение адсорбированных частиц А– на энергетической схеме определяется сродством молекул А к электрону Ee.aff. Энергия, выделяющаяся при хемосорбции первых молекул А, равна (рис.25.10, а). При хемосорбции следующих молекул А электроны поступают от донорных центров, лежащих более глубоко в кристалле, и поверхностный слой приобретает объемный заряд. Это энергетически затрудняет дальнейший переход электронов, уровень Ферми понижается. Когда энергия электронов твердого тела EF становится равной энергии электронов в адсорбированном веществе, достигается адсорбционное равновесие (рис. 25.10, б).
Согласно этой модели, положение уровня Ферми полупроводника определяет прочность и степень хемосорбции. Волькенштейн предложил различать три вида хемосорбции:
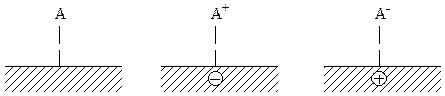
Слабая связь Сильная донорная связь Сильная акцепторная связь
При прочной хемосорбции из валентнонасыщенной молекулы образуется ион-радикал вследствие локализации свободного электрона или дырки, а из радикала получается валентнонасыщенная заряженная частица. Адсорбированные частицы сами действуют как доноры или акцепторы электронов и влияют на положение уровня Ферми полупроводника.
На поверхности могут находиться как активные, так и неактивные в отношении определенной реакции хемосорбированные частицы. При прочих одинаковых условиях скорость реакции будет определяться долей активных хемосорбированных частиц на поверхности. Так как доля хемосорбированных частиц изменяется с изменением положения уровня Ферми, изменять активность и селективность катализатора можно, влияя на положение уровня Ферми.
Общим итогом применения электронных представлений в гетерогенном катализе является вывод о том, что каталитическая активность прямо связана с числом свободных валентностей на поверхности катализатора. Однако все теоретические представления катализа на металлах и полупроводниках построены в основном на представлениях об идеальном кристалле с использованием зонной теории твердого тела, которая построена в одноэлектронном приближении. Поэтому нельзя давать количественную трактовку результатов, полученных на реальных катализаторах, с помощью приведенных выше подходов. Тем не менее, применение таких подходов может дать интересные качественные обобщения и является весьма перспективным. На настоящем этапе электронные теории оперируют пока с простейшими модельными системами. Но они дают новое истолкование уже сложившимся и апробированным понятиям, открывают путь к более глубокому познанию установленных фактов.
Полученные к настоящему времени экспериментальные данные и развитые теоретические представления значительно углубили наше понимание различных каталитических процессов. Если в прошлом отдельные катализаторы подбирались чисто эмпирически (например, Габер исследовал около 20 тысяч различных веществ в поисках первого промышленного катализатора для синтеза аммиака), то имеющиеся в настоящее время сведения о каталитических процессах дают критерии предварительного выбора катализатора и указывают пути создания эффективных каталитических систем. Однако окончательная доводка катализатора до промышленного использования по-прежнему решается лишь экспериментальным путем.
| <== предыдущая лекция | | | следующая лекция ==> |
| Основные результаты. | | | ТЕХНОЛОГІЧНІ ЛІНІЇ ДЛЯ ВИРОБНИЦТВА ЦЕМЕНТУ |
Дата добавления: 2015-12-16; просмотров: 1594;
