Определение температурных полей в форме при граничных условиях первого рода.

Пусть мы имеем форму начальная температура которой равна t_нф. В момент времени t = 0 температура на поверхности мгновенно изменя­ется и становится равной t_с и в дальнейшем не изменяется. Запишем математическую формулировку задачи

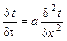
t_(х,t=0)=t_нф (8)

t_(х=0,t)=t_c

Данная система уравнений может быть решена или методом разделения переменных или с помощью рядов Фурье. Решение имеет вид:

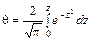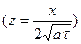, (9)

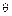- безразмерная относительная температура.

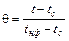(10)

Правая часть формулы (9) является табулированной функцией и называется функцией (или интегралом) ошибок и обозначается

.

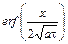Таким образом, решение задачи имеет вид :

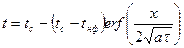, (11)

где значения интеграла ошибок в зависимости от значения ар­гумента 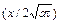может быть найдено по таблице (см. Приложение);

х - расстояние от поверхности формы;

t - температура на глубине х в момент времени t.

Схема установки для экспериментального определения темпера­турного поля формы представлена на рис.2.1. На форму 1 с темпера­турой сверху устанавливается массивная, теплоизолированная с по­верхности металлическая болванка с температурой t_c. На расстоянии через 5 мм от поверхности в форму вставлены термопары. Измерение температур производится с момента установки болванки с помощью электронного потенциометра ЭПП 09 в каждой точке через определен­ные промежутки времени, определяемые скоростью движения диаграмм­ной ленты, таким образом, на ленте записываются кривые изменения температуры в форме на различной глубине. Теоретические значения температур в этих точках получим при расчете по формуле (11). Значения х и t в формуле задаются преподавателем.

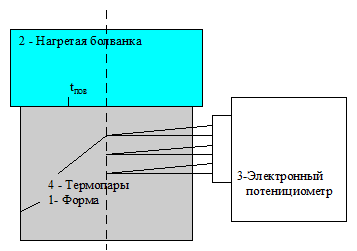
Рис.2.1. Схема экспериментального определения темпера­турного поля формы.