РАСЧЕТ ТЕМПЕРАТУРНЫХ ПОЛЕЙ В ЛИТЕЙНОЙ ФОРМЕ

Цель работы: Изучение процессов нестационарной теплопроводнос­ти применительно к процессам литья

1. Краткая теория

Если температурное поле изменяется во времени, то тепловые процессы, протекающие в таких условиях, называются нестационарны­ми. В практике литейного производства мы встречаемся чаще всего именно с такими процессами (плавление металла или сплава, запол­нение формы сплавом, кристаллизация отливки, охлаждение ее в фор­ме и на воздухе после выбивки, температурная обработка отливки, сушка стержней, прокалка форм и т.д.).

Передачу теплоты при нестационарном режиме можно определить, если найти закон изменения температурного поля и теплового потока во времени и пространстве

t=f(x,y,z,t) (1)

Q=f(x,y,z,t) (2)

Указанные зависимости могут быть найдены из решения дифферен­циального уравнения теплопроводности Фурье-Кирхгофа:

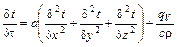(3)

При решении конкретной задачи, необходимо каким-то образом описать особенности данного явления. Это достигается путем добав­ления к дифференциальному уравнению условий однозначности.

Условия однозначности включают в себя:

1. Физические свойства тела или тел. При решении за­дач по определению параметров термической обработки, литья, сварки и т.п. это физические свойства металла или сплава в твердом и жидком состояниях, свойства формы и т.д.

2. Геометрические свойства тела. В которых задаются геометрические свойства тела.

3. Начальные условия. В которых задается распределение температур в телах в начальный момент времени. Например, температура заливки сплава, начальная температура формы.

4. Граничные условия, которые описывают особенности протекания процесса на границах тела. Граничные условия (ГУ) могут быть за­даны несколькими способами.

ГУ 1 рода. При этом задается распределение температуры на по­верхности тела для каждого момента времени

t_c=f(x,y,z,t) (4)

ГУ 2 рода. При этом задаются величины теплового потока для каждой точки поверхности тела и любого момента времени

q_c=f(x,y,z,t) (5)

ГУ 3 рода. При этом задаются температура окружающей среды и закон теплообмена между поверхностью тела и окружающей средой

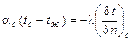(6)

ГУ 4 рода характеризуют условия теплообмена системы тел или тела с окружающей средой по закону теплопроводности

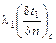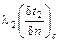= (7)

Таким образом, дифференциальное уравнение совместно с услови­ями однозначности дает полную математическую формулировку конк­ретной задачи теплопроводности. Поставленная задача разрешается аналитическим, численным или экспериментальным методом.