Порядок выполнения работы

Группа студентов (2-4 человека) последовательно выполняет две экспериментальные и две теоретические расчетные части работы.

Сначала определите экспериментально температурные поля в фор­ме, затем по формуле 11 рассчитайте теоретические значения темпе­ратур в форме. Постройте графики изменения температур на различ­ной глубине формы и сравните теоретические и экспериментальные значения.

Порядок оформления отчета

Отчет должен содержать

1. Название и цель работы.

2. Краткую теорию.

3. Схему и описание методики проведения экспериментов: опре­деление температурных полей формы.

4. Расчетные методики определения скорости кристаллизации и температурных полей формы.

5. Теоретические и расчетные графики скорости кристаллизации и температурных полей формы.

6. Выводы по работе.

Проверьте уровень вашей подготовки и усвоения материала.

1. Какие процессы мы называем стационарными и нестационарными.

2. Что такое условие однозначности.

3. Что характеризуют начальные условия.

4. Что характеризуют граничные условия, как их задают.

5. Что характеризует коэффициент температуропроводности.

6. Какие приближенные методы решения нестационарных тепловых задач вы знаете.

7. Охарактеризуйте метод конечных разностей.

8. В чем преимущества метода элементарных балансов.

9. Объясните сущность метода регулярного режима.

ПРАКТИЧЕСКАЯ РАБОТА № 3

РАСЧЕТ ВРЕМЕНИ НАГРЕВА ЗАГОТОВКИ

ДО ЗАДАННОЙ ТЕМПЕРАТУРЫ

Цель работы.

Ознакомление с методами решения дифференциального уравнения теплопроводности при граничных условиях III-рода для нестационарных тепловых процессов. Расчет времени нагрева заготовки простой геометрической формы под термическую обработку. Определение температурного перепада по сечению тела.

1.Краткая теория

Процессы теплопроводности, когда поле температуры в теле из­меняется не только в пространстве, но и во времени, называются нестационарными. Математически это описывается следующим уравне­нием:

t=f(x,y.z,t)

Среди прак­тических задач нестационарной теплопроводности важнейшее значение имеют две группы процессов:

- тело стремится к тепловому равновесию;

- температура тела претерпевает периодические изменения.

К первой группе относятся процессы прогрева или охлаждения тел, помещенных в среду с заданным тепловым состоянием, например, охлаждение тела в процессе закалки, охлаждение отливки в форме.

Ко второй группе относятся процессы в периодически действую­щих подогревателях, например, тепловой процесс регенераторов, на­садка которых периодически то нагревается, то охлаждается возду­хом.

Допустим, что тело, имеющее температуру t_н , поместили в сре­ду с температурой t_ж;(t_ж > t_н), сразу же между средой и телом возникает процесс теплообмена, и тело начинает прогреваться. При­чем, сначала нагреваются поверхностные слои, но постепенно про­цесс прогрева распространяется и в глубь тела. По мере нагрева температура в каждой точке асимптотически приближается к темпе­ратуре нагревающей среды; теоретически через большой промежуток времени тело прогревается полностью.

Таким образом, нестационарный тепловой процесс всегда связан с изменением энтальпии тела и им обуславливается. Так как ско­рость изменения энтальпии тела прямо пропорциональна способности материала проводить теплоту (т.е. теплопроводности l) и обратно пропорциональна его теплоаккумулирующей способности (т.е. объем­ной теплоемкости с×r), то в целом скорость теплового процесса при нестационарном режиме определяется значением температуропровод­ности a=l/(cr).

Решить задачу нестационарной теплопроводности - это значит найти зависимости изменения температуры и количества переданной теплоты во времени для любой точки тела. Такие зависимости могут быть получены путем решения общего дифференциального уравнения теплопроводности.

Однако такие решения получаются достаточно сложными даже для тел простой формы: пластины, цилиндра, шара.

При решении конкретных технических задач в большинстве случа­ев достаточно знать температуру на поверхности тела (t_c) и в его центре (t₀). В этом случае решение уравнения упрощается, искомые температуры являются функцией двух чисел подобия Био (В_i) и Фурье (F₀).

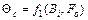
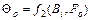
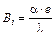
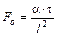
где a - коэффициент теплоотдачи, (Вт/(м²7⁰с);

l - характерный размер (для плоской стенки половина толщины, для цилиндра и шара радиус), м;

l - теплопроводность тела, Вт/(м7^оС);

а - температуропроводность материала , м²/с;

t - время, с.

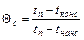
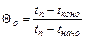
где 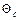- относительная температура поверхности тела;

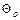- относительная температура центра тела;

t_п - температура печи, С;

t_конс и t_кон0 - конечная температура поверхности и центра тела ⁰С;

t_начс и t_нач0 - начальная температура поверхности и центра тела ⁰С.

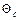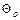По результатам решений построены специальные графики (номог­раммы Будрина), которые связывают основные параметры процесса. Относительную температуру ( или ) и число Био (В_i) и Фурье (F₀).

Рассмотрим физический смысл критериев В_i и F₀.

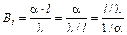
При второй записи в числителе выражения стоит коэффициент теплоотдачи (a), который характеризует интенсивность внешнего теплообмена, т.е. теплоотдачи от среды и поверхности тела (или наоборот). В знаменателе стоит величина отношения теплопроводнос­ти к характерному размеру тела, что определяет интенсивность внутреннего теплообмена между поверхностью тела и внутренними его слоями. Таким образом, критерий Био представляет собой отношение параметров, характеризующих интенсивность процессов внешнего и внутреннего теплообмена. При третьей записи числа видно, что критерий Био представляет собой отношение внутреннего теплового сопротивления к наружному. Обе эти формулировки позволяют заключить, что характер определе­ния температуры в объеме нагреваемого (охлаждаемого) тела опреде­ляется величиной критерия Био. Чем больше эта величина, тем боль­ше интенсивность внешнего теплообмена, по сравнению с интенсив­ностью внутреннего, то есть большим значениям критерия Био должна соответствовать меньшая равномерность распределения температуры в объеме тела на протяжении всего периода нагрева (охлаждения) и наоборот. Критерий Фурье, рассчитываемый по формуле:

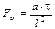
характеризует связь между скоростью изменения температурного по­ля, физическими параметрами тела и его размерами (критерий тепло­вой гомохронности). Достаточно часто его называют безразмерным временем, так как в сущности он характеризует временное пособие протекающих тепловых процессов.

2. Расчет времени, необходимого для нагрева поверхности те­ла определенной геометрической формы до заданной температуры.

Нагрев тела цилиндрической формы производится в печи сопротивления. Температура начальная тела (t_н), температура печи (t_п) и температура поверх­ности (t_конс) задаются преподавателем.

Определение времени необходимого для нагрева поверхности тела производится по формуле:

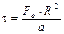(1)

где Fо - число Фурье, определяемое по номограмме Будрина см. Приложение;

R - радиус цилиндра (м);

a - температуропроводность материала цилиндра.

Для определения числа Fо необходимо рассчитать значения отно­сительной температуры и числа В_i. Относительная температура поверхности тела определяется по формулам:

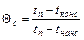(2)

а число Bi

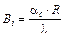(3)

где a_c - суммарный коэффициент теплообмена между поверхностью те­ла и атмосферой печи, равный 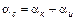(4)

где a_и - коэффициент теплоотдачи излучением;

a_к - конвективный коэффициент теплоотдачи.

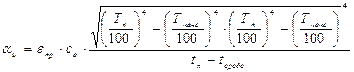, (5)

где с_o - коэффициент излучения абсолютно черного тела (с_o=5,67)

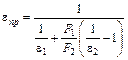, (6)

e₁ – степень черноты нагреваемого тела;

e₂ – степень черноты футеровки печи;

F₁ – площадь боковой поверхности тела (м²);

F₂ – площадь боковой поверхности печи (м²).

Конвективный коэффициент теплоотдачи может быть определен по формуле:

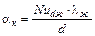, (7)

Nu_dж – число Нуссельта;

l_ж – теплопроводность воздуха при температуре печи;

d – диаметр цилиндра.

Число Нуссельта может быть рассчитано по уравнению подобия:

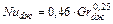(8)

которое верно при условии, что 10³ <Gr×Pr < 10⁸ где Pr - число Прандтля (для воздуха Рr = 0,7);

Gr_dж - число Грасгофа

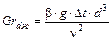(9)

b - термическое расширение (для воздуха b=0.00324)

g - ускорение свободного падения (м²/сек);

d - диаметр цилиндра (м);

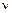- кинематическая вязкость воздуха при температуре печи (м² / с)

Dt=t_п-t_{сред с}

Таким образом, коэффициент теплоотдачи может быть найден по формуле:

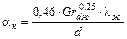(10)

Зная значения относительной температуры Q_c и числа Био (В_i), по номограмме Будрина см. Приложение определяется число Fо и рассчитывается время.

Значение суммарного коэффициента теплоотдачи может быть рассчитано по программе на микрокалькуляторе.